Trabajo de laboratorio №1.
Representación de pulsos periódicos
Señales cerca de Fourier.
Objetivo – Estudio de la composición espectral de una secuencia periódica de pulsos rectangulares a diferentes tasas de repetición y duraciones de pulso.
Introducción
Para la transmisión, almacenamiento y procesamiento de la información se utilizan señales de pulsos periódicos, los cuales pueden ser representados matemáticamente por series de Fourier. Hay un tiempo fig.1 y una representación de frecuencia de señales eléctricas fig.2.
Figura 1. Forma temporal de representación del periódico.
una secuencia de pulsos rectangulares.
La representación de una señal en el dominio del tiempo permite determinar sus parámetros, energía, potencia y duración. Las transformadas de Fourier se utilizan para representar señales en el dominio de la frecuencia como un espectro. El conocimiento de las propiedades de la frecuencia permite resolver los problemas de identificar las características de la señal (determinar sus parámetros más informativos), filtrar (seleccionar una señal útil contra un fondo de ruido) y elegir una frecuencia de muestreo de señal continua. Uno de los parámetros más importantes de la señal es el ancho del espectro de frecuencias, ya que es este parámetro el que resulta determinante a la hora de coordinar la señal con los equipos de procesamiento y transmisión de información.
Fórmulas básicas y definiciones.
función periódica Utah) con periodo T se puede representar mediante la serie de Fourier
(1)
vacilación 
con frecuencia se llama el primer armónico; (n=1) oscilación 
con una frecuencia - el segundo armónico (n = 2), 
con frecuencia - n-ésimo armónico.
Expresión (1) usando la identidad
se puede reescribir como
, (2)
Los coeficientes y están determinados por las fórmulas
El valor expresa el valor promedio de la función durante el período, también se le llama componente constante y se calcula mediante la fórmula
Las fórmulas (3) resuelven el problema análisis : para una función periódica dada, necesita encontrar los coeficientes de Fourier y . Las fórmulas (1) y (2) resuelven el problema del armónico síntesis : por los coeficientes dados y es necesario encontrar la función periódica .
Análisis del espectro de un tren de pulsos rectangulares
El conjunto de amplitudes y frecuencias de los componentes armónicos se llama respuesta de amplitud-frecuencia(AFC), y la dependencia de las frecuencias armónicas característica de frecuencia de fase (PFC). El espectro de amplitud-frecuencia de pulsos rectangulares se puede representar gráficamente en la Fig.2. 
Figura 2. Respuesta de frecuencia y respuesta de fase de una secuencia periódica
pulsos cuadrados.
Sea , que representa una secuencia de pulsos rectangulares en la Fig. 1 con amplitud , duración y período, descrita por la ecuación
Luego, las amplitudes y fases de los componentes armónicos están determinadas por la ecuación:
(4)
El valor se denomina ciclo de trabajo y se indica con la letra. Entonces las ecuaciones (4) toman la forma
donde n = 1, 2, … . (cinco)
Para calcular la potencia de las señales representadas por una serie de Fourier en teoría de la información se utilizan fórmulas en las que el valor de la resistencia es R = 1 Ohm. En este caso, los voltajes u y las corrientes i son iguales porque i = u/R.
La potencia de la componente constante P 0 será
y la potencia de la componente variable P n para el n-ésimo armónico
(6)
La fórmula de la potencia resultante tomará la forma
LA TAREA
1. Analizar un tren de pulso rectangular periódico
1.1 De acuerdo con el número de opción N recibido del docente, determine de la tabla 1 el valor del ciclo de trabajo y la frecuencia circular .
tabla 1
| No., var | q | , rad/s | No., var | q | , rad/s |
| 3,24 | 47,25 | 8,50 | 69,22 | ||
| 6,52 | 97,50 | 6,72 | 78,59 | ||
| 5,93 | 14,45 | 2,30 | 19,44 | ||
| 7,44 | 15,12 | 3,59 | 37,96 | ||
| 1,87 | 70,93 | 4,48 | 78,27 | ||
| 5,46 | 91,65 | 2,99 | 42,48 | ||
| 6,40 | 86,40 | 6,18 | 75,45 | ||
| 1,27 | 48,98 | 1,81 | 57,64 | ||
| 2,97 | 40,13 | 3,22 | 15,46 | ||
| 1,09 | 85,95 | 3,66 | 55,25 | ||
| 2,13 | 57,30 | 3,27 | 27,58 | ||
| 7,99 | 66,90 | 4,64 | 3,68 | ||
| 4,61 | 31,55 | 3,71 | 43,73 | ||
| 1,95 | 25,24 | 4,33 | 70,44 | ||
| 2,66 | 6,61 | 3,38 | 52,07 | ||
| 1,10 | 18,37 | 6,92 | 26,17 | ||
| 4,06 | 70,24 | 4,95 | 55,52 | ||
| 2,40 | 35,10 | 6,51 | 82,64 | ||
| 9,42 | 33,96 | 3,32 | 68,07 | ||
| 6,13 | 43,25 | 7,75 | 32,49 | ||
| 7,36 | 52,37 | 5,71 | 26,68 | ||
| 2,33 | 24,84 | 2,42 | 96,02 | ||
| 2,18 | 25,34 | 16,99 | 88,59 | ||
| 5,80 | 12,99 | 62,23 | 50,21 | ||
| 1,68 | 41,16 | 37,54 | 20,70 |
1.2 a) Determinar los primeros 11 valores de los coeficientes un (n=0, 1, 2, ..., 10), suponiendo E=1 V, usando hojas de cálculo de Excel (o una calculadora, u otro producto de software) usando las fórmulas (5 ) y e introdúzcalas en la línea correspondiente un de la Tabla 2.
1.3 b) Calcula las potencias p n y anótalas en la tabla 2.
Tabla 2
| w | 1 | 2w1 | … | 10w1 | |
| tú n | tu 0 | tu 1 | tu 2 | … | tu 10 |
| jn | j1 | j2 | J 3 | … | j 10 |
| pag norte | p0 | p1 | p2 | pág. 10 |
y un gráfico de la característica de amplitud-frecuencia (AFC) Fig. 3, a).
1.4 Construya una característica de frecuencia de fase (PFC) de un tren de pulsos periódicos como el de la figura 2) en el que un cambio en el signo de u n sea equivalente a un cambio de fase de p.
1.5 Calcule el espectro de potencia específico (en una resistencia de 1 Ohm) de los primeros 10 armónicos utilizando la fórmula
.
2. El problema de la síntesis.
2.1. Usando la ecuación (1), represente la suma de los primeros 10 armónicos sustituyendo en la ecuación
según los valores de u n calculados en la tabla para , , , …. y construir una dependencia del tiempo en el período T, por ejemplo.
de la tabla 3
en forma de gráfico 4 en el rango de tiempo de un período T= usando el tiempo actual t = nD t - t/2, con un paso donde n=0,1,2, …,10 mostrado en la fig. 3 .
Arroz. 3. Intervalo de tiempo para la síntesis de señales
Clasificación de las señales y sus parámetros.
Las señales eléctricas son procesos eléctricos utilizados para transmitir o almacenar información.
Las señales se pueden dividir en dos grandes clases: deterministas y aleatorias. Las señales se denominan deterministas si sus valores instantáneos en cualquier momento del tiempo se pueden predecir con una probabilidad igual a uno y que se dan como una cierta función definida del tiempo. Estos son algunos ejemplos típicos: una señal armónica con una amplitud conocida A y periodo T(Figura 1.1 pero); una secuencia de pulsos rectangulares con un período de repetición conocido T, duración t y amplitud A(Figura 1.1 B); una secuencia de pulsos de forma arbitraria con duración t y amplitud conocidas A y periodo T(Figura 1.1 en). Las señales deterministas no contienen ninguna información.
Las señales aleatorias son funciones caóticas del tiempo, cuyos valores no se conocen de antemano y no se pueden predecir con una probabilidad igual a uno (un solo pulso con duración t y amplitud A(Figura 1.1 GRAMO) habla, música en términos de cantidades eléctricas). Las señales aleatorias también incluyen ruido.
Las señales deterministas, a su vez, se subdividen en periódicas, para las cuales la condición S(t)=S(t+kT), donde T- período k-cualquier número entero, y S(t) se entiende como una corriente, voltaje o carga variable en el tiempo (Fig. 1.1 a B C).
Obviamente, cualquier señal determinista para la cual la condición S(t)¹ S(t+kT).
La señal periódica más simple es una señal armónica de la forma 
.
Cualquier señal periódica compleja se puede descomponer en componentes armónicos. A continuación, dicha descomposición se llevará a cabo para varios tipos específicos de señales.
Una señal armónica de alta frecuencia, en la que la información está incrustada por modulación, se denomina señal de radio (Fig. 1.1 D).
señales periódicas.
Cualquier señal periódica compleja S(t)=S(t+kT) (Fig. 1.2), dada en el intervalo de valores t de –¥ a +¥, se puede representar como una suma de señales armónicas elementales. Esta representación se realiza en forma de serie de Fourier, si solo la función periódica dada satisface las condiciones de Dirichlet:
1. En cualquier intervalo de tiempo finito, la función S(t) debe ser continua o tener un número finito de discontinuidades de primera clase.
2. Dentro de un período, la función debe tener un número finito de máximos y mínimos.
Por lo general, todas las señales de radio reales cumplen estas condiciones. En forma trigonométrica, la serie de Fourier tiene la forma (1.1)
donde la componente constante es 
(1.2)
y los coeficientes un , Y segundo norte para términos cosenos y sinusoidales, las expansiones están determinadas por las expresiones 
(1.3)
Amplitud (módulo) y fase (argumento) n-ésimo los armónicos se expresan en términos de coeficientes un , Y segundo norte de la siguiente manera 
(1.4)
Cuando se usa la notación compleja, la expresión de la señal S(t) toma la forma 
. Aquí los coeficientes 
, llamadas amplitudes complejas, son 
y están relacionados con los valores a n y b n por las fórmulas: para n>0, y para n<0. С учётом обозначений 
.
El espectro de una función periódica consta de líneas individuales correspondientes a frecuencias discretas 0, w, 2w, 3w ..., es decir, tiene una línea o carácter discreto (Fig. 1.3). El uso de series de Fourier en combinación con el principio de superposición es una poderosa herramienta para analizar la influencia de los sistemas lineales en el paso de varios tipos de señales periódicas a través de ellos.
Al expandir una función periódica en una serie de Fourier, se debe tener en cuenta la simetría de la función en sí, ya que esto nos permite simplificar los cálculos. Dependiendo del tipo de simetría, las funciones representadas por la serie de Fourier pueden:
1. 
No tiene componente constante si el área de la figura del semiciclo positivo es igual al área de la figura del semiciclo negativo.
2. No tienen armónicos pares y un componente constante, si los valores de la función se repiten después de medio período con el signo opuesto.
Composición espectral de una secuencia de pulsos rectangulares en diferentes períodos de su ciclo de trabajo.
Una secuencia periódica de pulsos rectangulares se muestra en la fig. 1.4. La componente constante de la serie de Fourier se determina a partir de la expresión y para este caso es igual a 
.
Amplitud cos-componente un es igual a
, y la amplitud de la componente sin segundo norte es igual a 
.
Amplitud norte armónico 
Desde la salida de la fuente del mensaje se reciben señales que transportan información, así como señales de reloj utilizadas para sincronizar el funcionamiento del transmisor y receptor del sistema de transmisión. Las señales de información tienen la forma de un reloj no periódico, una secuencia periódica de pulsos.
Para evaluar correctamente la posibilidad de transmitir dichos pulsos a través de canales de comunicación, determinemos su composición espectral. Una señal periódica en forma de pulsos de cualquier forma se puede expandir en una serie de Fourier según (7).
Las señales de diversas formas se utilizan para la transmisión por líneas de comunicación aérea y por cable. La elección de una forma u otra depende de la naturaleza de los mensajes transmitidos, el espectro de frecuencia de las señales, los parámetros de frecuencia y tiempo de las señales. Gran uso en la técnica de transmisión de mensajes discretos recibido señales de forma cercana a los pulsos rectangulares.
Calculemos el espectro, es decir conjunto de amplitudes de constante y
Componentes armónicos de pulsos rectangulares periódicos (Figura 4, a) con duración y periodo. Dado que la señal es una función par del tiempo, en la expresión (3) todos los componentes armónicos pares desaparecen ( 
=0), y las componentes impares toman los valores:
(10)
La componente constante es
(11)
Para una señal 1:1 (puntos de cable) Figura 4a:
,
.
(12)
Módulos de amplitudes de componentes espectrales de una secuencia de pulsos rectangulares con un período 
mostrado en la fig. 4b. La abscisa muestra la tasa de repetición del pulso principal 
() y frecuencias de componentes armónicos impares 
,
etc La envolvente del espectro cambia según la ley.
Con un aumento en el período, en comparación con la duración del pulso, aumenta el número de componentes armónicos en la composición espectral de la señal periódica. Por ejemplo, para una señal con periodo (Figura 4, c), obtenemos que la componente constante es igual a y
En la banda de frecuencia de cero a frecuencia, hay cinco componentes armónicos (Figura 4, d), mientras que solo hay uno.
Con un aumento adicional en el período de repetición del pulso, el número de componentes armónicos aumenta cada vez más. En el caso límite cuando 
la señal se convierte en una función no periódica del tiempo, el número de sus componentes armónicos en la banda de frecuencia de cero a frecuencia aumenta hasta el infinito; estarán ubicados a distancias infinitamente cercanas en frecuencia; el espectro de una señal no periódica se vuelve continuo.
Figura 4
2.4 Espectro de un solo pulso
Se establece un solo pulso de video (Figura 5):
Figura 5
El método de las series de Fourier permite una generalización profunda y fructífera, lo que hace posible obtener las características espectrales de señales no periódicas. Para ello, mentalmente suplementamos un solo pulso con los mismos pulsos que se suceden periódicamente a través de un cierto intervalo de tiempo, y obtenemos la secuencia periódica estudiada anteriormente:
Imaginemos un solo pulso como una suma de pulsos periódicos con un gran período.
,
(14)
donde están los números enteros.
Para una oscilación periódica
.
(15)
Para volver a un solo impulso, establezcamos el período de repetición en infinito: . Al hacerlo, obviamente:
,
(16)
Denotar
.
(17)
La cantidad es la característica espectral (función) de un solo pulso (transformada directa de Fourier). Depende únicamente de la descripción temporal del impulso y en general es complejo:
, (18) donde 
; (19)
; (20)
,
donde 
- módulo de la función espectral (característica amplitud-frecuencia del impulso);
- ángulo de fase, característica de frecuencia de fase del pulso.
Encontremos para un solo pulso por la fórmula (8), usando la función espectral:
.
Si obtenemos:
.
(21)
La expresión resultante se llama transformada inversa de Fourier.
La integral de Fourier define el momento como una suma infinita de componentes armónicos infinitesimales ubicados en todas las frecuencias.
Sobre esta base, se habla de un espectro continuo (continuo), que tiene un solo pulso.
La energía total del pulso (la energía liberada en la resistencia activa Ohm) es igual a
(22)
Cambiando el orden de integración, obtenemos
.
La integral interna es la función espectral del momento , tomada con el argumento -, es decir es la cantidad compleja conjugada: 
como consecuencia
El cuadrado del módulo (el producto de dos números complejos conjugados es igual al cuadrado del módulo).
En este caso, decimos condicionalmente que el espectro del pulso es de dos caras, es decir se encuentra en la banda de frecuencia de a.
La relación anterior (23), que establece la relación entre la energía del pulso (a una resistencia de 1 Ω) y el módulo de su función espectral, se conoce como igualdad de Parseval.
Establece que la energía contenida en el impulso es igual a la suma de las energías de todos los componentes de su espectro. La igualdad de Parseval caracteriza una importante propiedad de las señales. Si algún sistema selectivo transmite solo una parte del espectro de la señal, atenuando sus otros componentes, entonces esto significa que se pierde parte de la energía de la señal.
Dado que el cuadrado del módulo es una función par de la variable de integración, entonces, al duplicar el valor de la integral, se puede introducir la integración en el rango de 0 a:
.
(24)
En este caso, dicen que el espectro del pulso se encuentra en la banda de frecuencia de 0 a y se llama unilateral.
El integrando en (23) se denomina espectro de energía (densidad de energía espectral) del pulso
Caracteriza la distribución de la energía sobre la frecuencia, y su valor en una frecuencia es igual a la energía del pulso por banda de frecuencia de 1 Hz. Por lo tanto, la energía del pulso es el resultado de integrar el espectro de energía de la señal en todo el rango de frecuencia otdo, es decir, la energía es igual al área encerrada entre la curva que representa el espectro de energía de la señal y la abscisa eje.
Para evaluar la distribución de energía en el espectro, se utiliza la función integral relativa de la distribución de energía (característica de energía).
,
(25)
donde 
- energía de pulso en una banda de frecuencia dada de 0 a, que caracteriza la fracción de energía de pulso concentrada en el rango de frecuencia de 0 a.
Para pulsos únicos de varias formas, se cumplen las siguientes regularidades:
Literatura: [L.1], p.40
Como ejemplo, presentamos la expansión en una serie de Fourier de una secuencia periódica de pulsos rectangulares con amplitud , duración y período de repetición , simétrica alrededor de cero, es decir
, (2.10)
Aquí 
La expansión de tal señal en una serie de Fourier da
, (2.11)
donde esta el ciclo de trabajo.
Para simplificar la notación, podemos introducir la notación
, (2.12)
Entonces (2.11) se escribe como sigue
, (2.13)
En la fig. 2.3 muestra una secuencia de pulsos rectangulares. El espectro de la secuencia, así como cualquier otra señal periódica, es de naturaleza discreta (lineal).
La envolvente del espectro (Fig. 2.3, b) es proporcional a 
. La distancia a lo largo del eje de frecuencia entre dos componentes vecinas del espectro es , y entre dos valores cero (ancho del lóbulo del espectro) es . El número de componentes armónicos dentro de un lóbulo, incluido el valor cero a la derecha de la figura, es , donde el signo significa redondeo al número entero más cercano menos (si el ciclo de trabajo es un número fraccionario), o (si el ciclo de trabajo es valor entero). A medida que aumenta el período, la frecuencia fundamental 
disminuye, los componentes espectrales en el diagrama convergen, las amplitudes de los armónicos también disminuyen. En este caso, se conserva la forma del sobre.
Al resolver problemas prácticos de análisis espectral, se utilizan frecuencias cíclicas en lugar de frecuencias angulares. 
medido en hercios. Obviamente, la distancia entre armónicos vecinos en el diagrama será , y el ancho de un lóbulo del espectro será . Estos valores se muestran entre paréntesis en el diagrama.
En la ingeniería de radio práctica, en la mayoría de los casos, en lugar de la representación espectral (Fig. 2.3, b), se utilizan diagramas espectrales de los espectros de amplitud y fase. El espectro de amplitud de una secuencia de pulsos rectangulares se muestra en la fig. 2.3, c.
Obviamente, la envolvente del espectro de amplitud es proporcional a 
.
En cuanto al espectro de fase (Fig. 2.3, d), se cree que las fases iniciales de los componentes armónicos cambian abruptamente por el valor -π al cambiar el signo del sobre sinc kπ/q. Se supone que las fases iniciales de los armónicos del primer lóbulo son cero. Entonces las fases iniciales de los armónicos del segundo lóbulo serán φ = -π , tercer pétalo φ = -2π etc
Considere otra representación de la señal por una serie de Fourier. Para ello utilizamos la fórmula de Euler
.
De acuerdo con esta fórmula, la k-ésima componente (2.9) de la expansión de la señal en una serie de Fourier se puede representar de la siguiente manera
; 
. (2.15)
Aquí, las cantidades y son complejas y representan las amplitudes complejas de los componentes del espectro. Entonces la serie
Fourier (2.8), teniendo en cuenta (2.14), toma la siguiente forma
, (2.16)
, (2.17)
Es fácil comprobar que la expansión (2.16) se realiza en función de las funciones de base 
, que también son ortogonales en el intervalo 
, es decir.
La expresión (2.16) es forma compleja Serie de Fourier que se extiende a frecuencias negativas. cantidades y 
, donde denota el complejo conjugado de una cantidad, se denominan amplitudes complejas espectro. Porque es una cantidad compleja, se sigue de (2.15) que
Y 
.
Entonces el conjunto es la amplitud y el conjunto es el espectro de fase de la señal.
En la fig. 2.4 muestra el diagrama espectral del espectro de la secuencia anterior de pulsos rectangulares, representado por la serie compleja de Fourier
El espectro también tiene un carácter de línea, pero a diferencia de los espectros considerados anteriormente, se determina tanto en la región de frecuencias positivas como en la región de frecuencias negativas. Dado que es una función par del argumento , el diagrama espectral es simétrico con respecto a cero.
Con base en (2.15), podemos establecer una correspondencia entre los coeficientes y y las expansiones (2.3). Porque
Y 
,
entonces como resultado obtenemos
. (2.18)
Las expresiones (2.5) y (2.18) nos permiten encontrar los valores en cálculos prácticos.
Demos una interpretación geométrica de la forma compleja de la serie de Fourier. Destaquemos el k-ésimo componente del espectro de la señal. En forma compleja, el k-ésimo componente se describe mediante la fórmula
donde y están determinados por las expresiones (2.15).
En el plano complejo, cada uno de los términos de (2.19) se representa como vectores de longitud 
, girado en un ángulo y en relación con el eje real y girando en direcciones opuestas con frecuencia (Fig. 2.5).
Obviamente, la suma de estos vectores da un vector situado en el eje real, cuya longitud es . Pero este vector corresponde a la componente armónica
En cuanto a las proyecciones de vectores sobre el eje imaginario, estas proyecciones tienen igual longitud, pero direcciones opuestas y suman cero. Esto significa que las señales presentadas en forma compleja (2.16) son de hecho señales reales. En otras palabras, la forma compleja de la serie de Fourier es matemático abstracción, que es muy conveniente para resolver una serie de problemas de análisis espectral. Por lo tanto, a veces el espectro definido por la serie trigonométrica de Fourier se llama espectro físico, y la forma compleja de la serie de Fourier es espectro matemático.
En conclusión, consideremos el tema de la energía y la distribución de potencia en el espectro de una señal periódica. Para hacer esto, usamos la igualdad de Parseval (1.42). Cuando la señal se expande en una serie trigonométrica de Fourier, la expresión (1.42) toma la forma
.
energía CC
,
y la energía del k-ésimo armónico
.
Entonces la energía de la señal
. (2.20)
Porque fuerza de señal promedio
,
entonces, teniendo en cuenta (2.18),
. (2.21)
Cuando la señal se expande en una serie compleja de Fourier, la expresión (1.42) tiene la forma
,
donde 
es la energía del k-ésimo armónico.
La energía de la señal en este caso
,
y su potencia media
.
De las expresiones anteriores se deduce que la energía o potencia media de la componente espectral k-ésima del espectro matemático es la mitad de la energía o potencia de la componente espectral correspondiente del espectro físico. Esto se debe al hecho de que el espectro físico se distribuye por igual entre el espectro matemático.
| -τ y /2 |
| τ y /2 |
| T |
| t |
| tu 0 |
| S t) |
Tarea No. 1, grupo RI - 210701
La representación espectral de las funciones de tiempo es ampliamente utilizada en la teoría de la comunicación. Para estudios teóricos y experimentales de las características de los circuitos eléctricos y transmisión de mensajes a través de canales de comunicación, se utilizan varios tipos de señales: oscilaciones armónicas, niveles de voltajes constantes, secuencias de pulsos rectangulares y de radio, etc. Señales computacionales en forma de La función unitaria juega un papel particularmente importante en los estudios teóricos de los circuitos eléctricos y la función de impulso (funciones de Dirac). Determinemos los espectros de las señales típicas más comunes.
11.1 Espectro de un tren de pulsos rectangulares
Sea una secuencia periódica de pulsos rectangulares con período T, duración de pulso t y amplitud A. La expresión analítica para la función que describe el pulso en el segmento tiene la forma
(11.1)
El gráfico de la secuencia periódica de pulsos se muestra en la Figura 11.1.
Figura 11.1
Esta función es par, ya que su gráfica es simétrica con respecto al eje y. Luego, los coeficientes de Fourier de esta función se calculan mediante las fórmulas (KFT2), donde .
El número representa el valor promedio de la función durante el período y se llama componente constante. La frecuencia se llama fundamental, o primer armónico, y las frecuencias k son armónicos superiores, donde k = 2,3,4,...
Construyamos el espectro de amplitud de la secuencia considerada de pulsos rectangulares. Dado que la función es periódica, su espectro de amplitud es similar a una línea. Indicar por la distancia entre los armónicos vecinos. Obviamente es igual a . La amplitud del k-ésimo armónico según (11.2) tiene la forma
(11.3)
Encontremos la relación entre el período T y la duración del pulso , en el que desaparece la amplitud del k-ésimo armónico.
A 2 ≈32V, A 3 ≈15V, A 4 ≈0, A 5 ≈6.36V, A 6 ≈10.5V, A 7 ≈6.36V, A 8 ≈0, A 9 ≈4.95V, A 10 ≈6.37V.
El espectro de amplitud obtenido como resultado del cálculo se muestra en la Figura 11.2.
Figura 11.2
Tal espectro se llama línea o espectro discreto.
Los espectros para q=8 y q=16 se calculan y representan de manera similar. Se muestran en las figuras 11.3 y 11.4 respectivamente.
Figura 11.3
Figura 11.4
Se puede ver en la figura que cuanto mayor es el ciclo de trabajo de los pulsos rectangulares, menos importante es la amplitud del primer armónico, pero más lentamente disminuye el espectro.
11.2 Espectro de un solo pulso rectangular
Considere Ф (11.1) para el caso en que Т→∞, es decir, una secuencia periódica de pulsos degenera en un solo pulso rectangular, de duración t u .
La expresión analítica para este impulso se escribe como:
La gráfica de esta función se muestra en la figura 11.5.
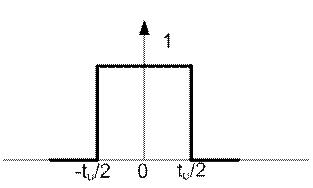
Figura 11.5
En este caso, la frecuencia del primer armónico y la distancia entre armónicos se vuelve igual a 0, por lo tanto, el espectro pasa de ser discreto a continuo, que consiste en un número infinito de líneas espectrales ubicadas a distancias infinitesimales entre sí. Tal espectro se llama continuo. Esto implica la regla más importante: las señales periódicas generan espectros discretos y las señales no periódicas, continuas (continuas).
El espectro de un solo pulso rectangular se puede encontrar directamente a partir de la transformada directa de Fourier (10.1)