Puna laboratorike nr. 1.
Paraqitja e pulsit periodik
Sinjalet pranë Fourierit.
Objektiv - Studimi i përbërjes spektrale të një sekuence periodike pulsesh drejtkëndëshe me ritme të ndryshme përsëritjeje dhe kohëzgjatje pulsi.
Prezantimi
Për transmetimin, ruajtjen dhe përpunimin e informacionit, përdoren sinjale impulse periodike, të cilat mund të përfaqësohen matematikisht nga seritë Fourier. Ekziston një figurë e përkohshme 1 dhe një paraqitje e frekuencës së sinjaleve elektrike figura 2.
Fig. 1. Prezantimi i përkohshëm i periodikëve
sekuenca pulsesh drejtkëndëshe.
Përfaqësimi i sinjalit në fushën e kohës ju lejon të përcaktoni parametrat, energjinë, fuqinë dhe kohëzgjatjen e tij. Transformimet Furier përdoren për të përfaqësuar sinjalet në fushën e frekuencës si spektër. Njohja e vetive të frekuencës na lejon të zgjidhim problemet e identifikimit të karakteristikave të sinjalit (përcaktimi i parametrave të tij më informues), filtrimi (izolimi i një sinjali të dobishëm në sfondin e zhurmës) dhe zgjedhjen e frekuencës së kampionimit të një sinjali të vazhdueshëm. Një nga parametrat më të rëndësishëm të sinjalit është gjerësia e spektrit të frekuencës, pasi është ky parametër që rezulton të jetë vendimtar në përputhjen e sinjalit me pajisjet për përpunimin dhe transmetimin e informacionit.
Formulat dhe përkufizimet bazë.
Funksioni periodik u (t) me periodë T mund të përfaqësohet nga seria Fourier
(1)
Lëkundje 
me një frekuencë të quajtur harmonika e parë; (n = 1) tundet 
me frekuencë - harmonik i dytë (n = 2), 
me frekuencë - harmonike n-të.
Shprehja (1) duke përdorur identitetin
mund të rishkruhet si
, (2)
Koeficientët dhe përcaktohen nga formula
Sasia shpreh vleren mesatare te funksionit gjate periudhes, quhet edhe komponent konstant dhe llogaritet me formulen
Formulat (3) zgjidhin problemin analiza : për një funksion të caktuar periodik, ju duhet të gjeni koeficientët Fourier dhe. Formulat (1) dhe (2) zgjidhin problemin e harmonikës sinteza : nga koeficientët e dhënë dhe duhet të gjeni funksionin periodik.
Analiza e spektrit të një treni pulsi drejtkëndor
Bashkësia e amplitudave dhe frekuencave të komponentëve harmonikë quhet përgjigje amplitudë-frekuencë(AFC), dhe varësia nga frekuencat harmonike karakteristikë e frekuencës së fazës (PFC). Spektri i amplitudës-frekuencës së impulseve drejtkëndëshe mund të paraqitet grafikisht në Fig. 2. 
Fig. 2. Përgjigja e frekuencës dhe përgjigja fazore e një sekuence periodike
pulset drejtkëndëshe.
Le të përshkruhet nga ekuacioni, që përfaqëson një sekuencë pulsesh drejtkëndëshe në Fig. 1 me amplitudë, kohëzgjatje dhe periudhë
Pastaj amplituda dhe fazat për komponentët harmonikë përcaktohen nga ekuacioni:
(4)
Vlera quhet cikli i punës dhe shënohet me një shkronjë. Pastaj ekuacionet (4) marrin formën
ku n = 1, 2,…. (5)
Për të llogaritur fuqinë e sinjaleve të paraqitura nga seria Fourier në teorinë e informacionit, përdoren formula në të cilat vlera e rezistencës është R = 1 Ohm. Në këtë rast, tensionet u dhe rrymat i janë të barabarta, pasi i = u / R.
Fuqia e komponentit konstant P 0 do të jetë
dhe fuqia e komponentës së ndryshueshme P n për harmonikën e n-të
(6)
Formula për fuqinë që rezulton do të marrë formën
USHTRIMI
1. Kryeni një analizë periodike të valëve katrore
1.1 Me numrin e opsionit N, të marrë nga mësuesi, përcaktoni nga tabela 1 vlerën e ciklit të detyrës dhe frekuencën këndore .
Tabela 1
| Nr., var | q | , rad / s | Nr., var | q | , rad / s |
| 3,24 | 47,25 | 8,50 | 69,22 | ||
| 6,52 | 97,50 | 6,72 | 78,59 | ||
| 5,93 | 14,45 | 2,30 | 19,44 | ||
| 7,44 | 15,12 | 3,59 | 37,96 | ||
| 1,87 | 70,93 | 4,48 | 78,27 | ||
| 5,46 | 91,65 | 2,99 | 42,48 | ||
| 6,40 | 86,40 | 6,18 | 75,45 | ||
| 1,27 | 48,98 | 1,81 | 57,64 | ||
| 2,97 | 40,13 | 3,22 | 15,46 | ||
| 1,09 | 85,95 | 3,66 | 55,25 | ||
| 2,13 | 57,30 | 3,27 | 27,58 | ||
| 7,99 | 66,90 | 4,64 | 3,68 | ||
| 4,61 | 31,55 | 3,71 | 43,73 | ||
| 1,95 | 25,24 | 4,33 | 70,44 | ||
| 2,66 | 6,61 | 3,38 | 52,07 | ||
| 1,10 | 18,37 | 6,92 | 26,17 | ||
| 4,06 | 70,24 | 4,95 | 55,52 | ||
| 2,40 | 35,10 | 6,51 | 82,64 | ||
| 9,42 | 33,96 | 3,32 | 68,07 | ||
| 6,13 | 43,25 | 7,75 | 32,49 | ||
| 7,36 | 52,37 | 5,71 | 26,68 | ||
| 2,33 | 24,84 | 2,42 | 96,02 | ||
| 2,18 | 25,34 | 16,99 | 88,59 | ||
| 5,80 | 12,99 | 62,23 | 50,21 | ||
| 1,68 | 41,16 | 37,54 | 20,70 |
1.2 a) Përcaktoni 11 vlerat e para të koeficientëve un (n = 0, 1, 2, ..., 10), duke numëruar E = 1 V, duke përdorur tabelën e Excel (ose kalkulatorin, ose produktin tjetër softuer) sipas te formulat (5) dhe futini ato në rreshtin përkatës un të tabelës 2.
1.3 b) Llogaritni fuqitë p n dhe shkruani në tabelën 2.
tabela 2
| w | w 1 | 2w 1 | … | 10 w 1 | |
| u n | u 0 | ju 1 | ju 2 | … | ju 10 |
| j n | j 1 | j 2 | j 3 | … | j 10 |
| p n | p 0 | f 1 | f 2 | f 10 |
dhe grafiku i karakteristikës amplitudë-frekuencë (AFC) Fig. 3, a).
1.4 Paraqitni karakteristikën e frekuencës fazore (PFC) të një sekuence periodike pulsesh të ngjashme me Fig. 2) në të cilën një ndryshim në shenjën e u n është i barabartë me një zhvendosje fazore me p.
1.5 Llogaritni fuqinë specifike (me një rezistencë prej 1 Ohm) të spektrit të 10 harmonikave të para duke përdorur formulën
.
2. Problemi i sintezës.
2.1. Duke përdorur ekuacionin (1), përfaqësoni shumën e 10 harmonikave të para duke zëvendësuar ekuacionin
sipas vlerave të llogaritura të u n për,,,…. dhe vizatoni varësinë kohore nga periudha T, për shembull.
nga tabela 3
në formën e grafikut 4 në intervalin kohor të një periudhe T =, duke përdorur kohën aktuale t = nD t - t / 2, me një hap ku n = 0,1,2, ..., 10 treguar në Fig. 3.
Oriz. 3. Intervali kohor për sintezën e sinjalit
Klasifikimi i sinjaleve dhe parametrat e tyre.
Sinjalet elektrike janë procese elektrike që përdoren për të transmetuar ose ruajtur informacionin.
Sinjalet mund të ndahen në dy klasa të mëdha: përcaktuese dhe të rastësishme. Sinjalet përcaktuese janë ato, vlerat e çastit të të cilëve në çdo moment të kohës mund të parashikohen me një probabilitet të barabartë me një dhe të cilat jepen në formën e një funksioni të caktuar të caktuar kohe. Këtu janë disa shembuj tipikë: një sinjal harmonik me një amplitudë të njohur A dhe periudha T(fig. 1.1 a); sekuencë pulsesh drejtkëndëshe me një periudhë të njohur përsëritjeje T, kohëzgjatja t dhe dhe amplituda A(fig. 1.1 b); sekuencë pulsesh me formë arbitrare me kohëzgjatje t dhe amplitudë të njohur A dhe periudha T(fig. 1.1 v). Sinjalet përcaktuese nuk përmbajnë asnjë informacion.
Sinjalet e rastësishme janë funksione kaotike të kohës, vlerat e të cilave janë të panjohura paraprakisht dhe nuk mund të parashikohen me një probabilitet të barabartë me unitetin (një impuls i vetëm me kohëzgjatje t dhe amplitudë A(fig. 1.1 G) të folurit, muzika në shprehjen e madhësive elektrike). Sinjalet e rastësishme përfshijnë gjithashtu zhurmën.
Sinjalet përcaktuese, nga ana tjetër, ndahen në ato periodike, për të cilat kushti S(t)=S(t + kT), ku T- periudha, k-çdo numër i plotë, dhe nën S(t) kuptohet si një rrymë, tension ose ngarkesë që ndryshon me kalimin e kohës (Fig.1.1 a B C).
Natyrisht, çdo sinjal përcaktues për të cilin gjendja S(t)¹ S(t + kT).
Sinjali periodik më i thjeshtë është një sinjal harmonik i formës 
.
Çdo sinjal periodik kompleks mund të zbërthehet në komponentë harmonikë. Më poshtë, një dekompozim i tillë do të kryhet për disa lloje specifike sinjalesh.
Një sinjal harmonik me frekuencë të lartë, në të cilin informacioni është i ngulitur nga modulimi, quhet sinjal radio (Fig.1.1. d).
Sinjalet periodike.
Çdo sinjal kompleks periodik S(t)=S(t + kT) (Figura 1.2), e vendosur në diapazonin e vlerave t nga - ¥ në + ¥, mund të përfaqësohet si një shumë e sinjaleve elementare harmonike. Ky paraqitje kryhet në formën e një serie Furier, nëse vetëm funksioni periodik i dhënë plotëson kushtet e Dirichlet:
1. Në çdo interval kohor të fundëm, funksioni S(t) duhet të jetë i vazhdueshëm ose të ketë një numër të kufizuar ndërprerjesh të llojit të parë.
2. Brenda një periudhe, funksioni duhet të ketë një numër të kufizuar maksimalesh dhe minimale.
Në mënyrë tipike, të gjitha sinjalet reale të radios i plotësojnë këto kushte. Në formë trigonometrike, seria Fourier ka formën (1.1)
ku është komponenti konstant 
(1.2)
dhe koeficientët një n, dhe b n për termat kosinus dhe sinusoidal të zgjerimit përcaktohen nga shprehjet 
(1.3)
Amplituda (moduli) dhe faza (argumenti) n-të harmonikët shprehen në terma të koeficientëve një n, dhe b n në mënyrën e mëposhtme 
(1.4)
Kur përdoret forma komplekse e shkrimit, shprehja për sinjalin S (t) merr formën 
... Këtu janë koeficientët 
, të quajtura amplituda komplekse, janë të barabarta me 
dhe janë të lidhura me sasitë a n dhe b n me formulat: për n> 0, dhe për n<0. С учётом обозначений 
.
Spektri i një funksioni periodik përbëhet nga linja të veçanta që i korrespondojnë frekuencave diskrete 0, w, 2w, 3w ..., domethënë ka një karakter linear ose diskret (Fig. 1.3). Përdorimi i serive Fourier në kombinim me parimin e mbivendosjes është një mjet i fuqishëm për të analizuar ndikimin e sistemeve lineare në kalimin e llojeve të ndryshme të sinjaleve periodike nëpër to.
Kur zgjeroni një funksion periodik në një seri Fourier, duhet të merrni parasysh simetrinë e vetë funksionit, pasi kjo ju lejon të thjeshtoni llogaritjet. Në varësi të llojit të simetrisë, funksionet e paraqitura nga seria Fourier mund të:
1. 
Mos keni një komponent konstant nëse sipërfaqja e figurës për gjysmëperiudhën pozitive është e barabartë me sipërfaqen e figurës për gjysmëperiudhën negative.
2. Të mos ketë as harmonikë dhe komponentë konstante, nëse vlerat e funksionit përsëriten pas gjysmës së periodës me shenjën e kundërt.
Përbërja spektrale e një sekuence pulsesh drejtkëndëshe në periudha të ndryshme të ciklit të tyre të punës.
Një sekuencë periodike e pulseve drejtkëndore është paraqitur në Fig. 1.4. Përbërësi konstant i serisë Fourier përcaktohet nga shprehja dhe për këtë rast është e barabartë me 
.
Amplituda e bashkë-komponentëve a nështë e barabartë me
, dhe amplituda e komponentit të mëkatit b nështë e barabartë me 
.
Amplituda n-th harmonik 
Nga dalja e burimit të mesazhit, merren sinjale që bartin informacion, si dhe sinjale të orës që përdoren për të sinkronizuar funksionimin e transmetuesit dhe marrësit të sistemit të transmetimit. Sinjalet e informacionit janë në formën e jo periodike, dhe sinjalet e orës janë në formën e një sekuence periodike të pulseve.
Për të vlerësuar saktë mundësinë e transmetimit të pulseve të tilla përmes kanaleve të komunikimit, le të përcaktojmë përbërjen e tyre spektrale. Një sinjal periodik në formën e pulseve të çdo forme mund të zgjerohet në një seri Fourier sipas (7).
Për transmetimin përmes linjave të komunikimit me ajër dhe kabllo, përdoren sinjale të formave të ndryshme. Zgjedhja e një forme ose një tjetër varet nga natyra e mesazheve të transmetuara, spektri i frekuencës së sinjaleve, frekuenca dhe parametrat kohorë të sinjaleve. Sinjalet e ngjashme në formë me pulset drejtkëndore përdoren gjerësisht në teknologjinë e transmetimit të mesazheve diskrete.
Le të llogarisim spektrin, d.m.th. bashkësia e amplitudave të konstantës dhe
komponentët harmonikë të pulseve periodike drejtkëndore (Figura 4, a) me kohëzgjatje dhe periodë. Meqenëse sinjali është një funksion i barabartë i kohës, atëherë në shprehjen (3) të gjithë komponentët harmonikë zhduken ( 
= 0), dhe komponentët teke marrin vlerat:
(10)
Komponenti konstant është
(11)
Për një sinjal 1: 1 (pika CW) Figura 4a:
,
.
(12)
Modulet e amplitudave të përbërësve spektralë të një sekuence pulsesh drejtkëndëshe me një periodë 
janë paraqitur në Fig. 4, b. Abshisa tregon shkallën kryesore të përsëritjes së pulsit 
() dhe frekuencat e komponentëve harmonikë tek 
,
etj. Zarfi i spektrit ndryshon sipas ligjit.
Me një rritje të periudhës, në krahasim me kohëzgjatjen e pulsit, rritet numri i përbërësve harmonikë në përbërjen spektrale të sinjalit periodik. Për shembull, për një sinjal me një periudhë (Figura 4, c), marrim se komponenti konstant është i barabartë me dhe
Në brezin e frekuencës nga zero në frekuencë, ka pesë komponentë harmonikë (Figura 4, d), ndërsa ka vetëm një.
Me një rritje të mëtejshme të periudhës së përsëritjes së pulsit, numri i përbërësve harmonikë bëhet gjithnjë e më shumë. Në rastin kufizues kur 
sinjali bëhet një funksion jo periodik i kohës, numri i përbërësve të tij harmonikë në brezin e frekuencës nga zero në frekuencë rritet në pafundësi; ato do të vendosen në distanca pafundësisht të afërta të frekuencës; spektri i sinjalit jo periodik bëhet i vazhdueshëm.
Figura 4
2.4 Spektri i pulsit të vetëm
Është vendosur një puls i vetëm video (Figura 5):
Figura 5
Metoda e serisë Fourier lejon një përgjithësim të thellë dhe të frytshëm, i cili bën të mundur marrjen e karakteristikave spektrale të sinjaleve jo periodike. Për ta bërë këtë, plotësoni mendërisht një puls të vetëm me të njëjtat impulse, duke ndjekur periodikisht në një interval të caktuar kohor, dhe ne do të marrim sekuencën periodike të studiuar më parë:
Le të imagjinojmë një puls të vetëm si shuma e pulseve periodike me një periodë të madhe.
,
(14)
ku janë numrat e plotë.
Për lëkundje periodike
.
(15)
Për t'u kthyer në një impuls të vetëm, le ta drejtojmë periudhën e përsëritjes në pafundësi:. Në këtë rast, është e qartë:
,
(16)
shënojmë
.
(17)
Sasia quhet karakteristikë (funksion) spektrale e një impulsi të vetëm (transformimi i drejtpërdrejtë i Furierit). Varet vetëm nga përshkrimi i përkohshëm i impulsit dhe, në përgjithësi, është kompleks:
, (18) ku 
; (19)
; (20)
,
ku 
- moduli i funksionit spektral (karakteristikë amplitudë-frekuencë e pulsit);
- këndi i fazës, karakteristikë e frekuencës fazore të pulsit.
Gjeni për një impuls të vetëm sipas formulës (8) duke përdorur funksionin spektral:
.
Nëse, marrim:
.
(21)
Shprehja që rezulton quhet transformim i anasjelltë i Furierit.
Integrali Furier e përcakton momentin si një shumë e pafundme e komponentëve harmonikë infinitimalë të vendosur në të gjitha frekuencat.
Mbi këtë bazë, flitet për një spektër të vazhdueshëm (të vazhdueshëm) të zotëruar nga një puls i vetëm.
Energjia totale e pulsit (energjia e lëshuar në rezistencën aktive Ohm) është e barabartë me
(22)
Duke ndryshuar rendin e integrimit, marrim
.
Integrali i brendshëm është funksioni spektral i momentit të marrë me argumentin -, d.m.th. është një sasi komplekse e konjuguar: 
Prandaj
Moduli në katror (produkti i dy numrave kompleksë të konjuguar është i barabartë me modulin në katror).
Në këtë rast, në mënyrë konvencionale thuhet se spektri i pulsit është i dyanshëm, d.m.th. ndodhet në brezin e frekuencës nga deri në.
Lidhja e mësipërme (23), e cila vendos marrëdhënien midis energjisë së pulsit (në një rezistencë prej 1 Ohm) dhe modulit të funksionit të tij spektral, njihet si barazia e Parsevalit.
Ai thotë se energjia që përmban një impuls është e barabartë me shumën e energjive të të gjithë përbërësve të spektrit të tij. Barazia e Parseval karakterizon një veti të rëndësishme të sinjaleve. Nëse një sistem zgjedhor kalon vetëm një pjesë të spektrit të sinjalit, duke zbutur komponentët e tjerë të tij, atëherë kjo do të thotë se një pjesë e energjisë së sinjalit humbet.
Meqenëse katrori i modulit është një funksion çift i ndryshores së integrimit, atëherë duke dyfishuar vlerën e integralit, integrimi mund të futet në intervalin nga 0 në:
.
(24)
Në këtë rast, ata thonë se spektri i pulsit ndodhet në brezin e frekuencës nga 0 në dhe quhet i njëanshëm.
Integrandi në (23) quhet spektri i energjisë (densiteti i energjisë spektrale) i pulsit
Karakterizon shpërndarjen e energjisë mbi frekuencë, dhe vlera e saj në një frekuencë është e barabartë me energjinë e pulsit për brezin e frekuencës 1 Hz. Prandaj, energjia e pulsit është rezultat i integrimit të spektrit energjetik të sinjalit në të gjithë diapazonin e frekuencës veçmas; me fjalë të tjera, energjia është e barabartë me zonën e mbyllur midis kurbës që përfaqëson spektrin energjetik të sinjalit dhe boshtit të abshisës.
Për të vlerësuar shpërndarjen e energjisë në spektër, përdorni funksionin integral relativ të shpërndarjes së energjisë (karakteristika e energjisë)
,
(25)
ku 
është energjia e pulsit në një brez të caktuar frekuence nga 0 në, e cila karakterizon fraksionin e energjisë së pulsit të përqendruar në diapazonin e frekuencës nga 0 në.
Për impulset e vetme të formave të ndryshme, plotësohen rregullsitë e mëposhtme:
Literatura: [L.1], f. 40
Si shembull, le të paraqesim zgjerimin e serisë Fourier të një sekuence periodike pulsesh drejtkëndëshe me amplitudë, kohëzgjatje dhe periudhë përsëritjeje simetrike rreth zero, d.m.th.
, (2.10)
Këtu 
Zgjerimi i një sinjali të tillë në një seri Fourier jep
, (2.11)
ku është cikli i punës.
Për të thjeshtuar shënimin, mund të futni shënimin
, (2.12)
Atëherë (2.11) mund të shkruhet si më poshtë
, (2.13)
Në fig. 2.3 tregon një sekuencë pulsesh drejtkëndëshe. Spektri i një sekuence, si çdo sinjal tjetër periodik, është diskret (linear).
Zarfi i spektrit (Fig. 2.3, b) është proporcional me 
... Distanca përgjatë boshtit të frekuencës midis dy përbërësve ngjitur të spektrit është e barabartë, dhe midis dy vlerave zero (gjerësia e lobit të spektrit) -. Numri i komponentëve harmonikë brenda një petal, duke përfshirë vlerën zero në të djathtë në figurë, është, ku shenja nënkupton rrumbullakimin në numrin e plotë më të afërt, më pak (nëse cikli i punës është një numër i pjesshëm), ose (me një vlerë të plotë të ciklit të punës). Me një rritje të periudhës, frekuenca themelore 
zvogëlohet, komponentët spektralë në diagram afrohen me njëri-tjetrin, zvogëlohen edhe amplituda e harmonikëve. Në këtë rast, forma e zarfit ruhet.
Gjatë zgjidhjes së problemeve praktike të analizës spektrale, në vend të frekuencave këndore, përdoren frekuenca ciklike. 
matur në Hertz. Natyrisht, distanca midis harmonikave ngjitur në diagram do të jetë, dhe gjerësia e një lobi të spektrit do të jetë. Këto vlera tregohen në diagramin në kllapa.
Në inxhinierinë praktike të radios, në shumicën e rasteve, në vend të paraqitjes spektrale (Fig. 2.3, b), përdoren diagramet spektrale të spektrit të amplitudës dhe fazës. Spektri i amplitudës së një sekuence pulsesh drejtkëndëshe është paraqitur në Fig. 2.3, c.
Natyrisht, mbështjellja e spektrit të amplitudës është proporcionale me 
.
Sa i përket spektrit fazor (Fig. 2.3, d), besohet se fazat fillestare të komponentëve harmonikë ndryshojnë befas nga sasia -π kur ndryshoni shenjën e zarfit sinc kπ / q... Fazat fillestare të harmonikëve të lobit të parë supozohen të jenë zero. Atëherë do të jenë fazat fillestare të harmonikave të lobit të dytë φ = -π , petali i tretë φ = -2π etj.
Le të shqyrtojmë një paraqitje tjetër të sinjalit nga seria Fourier. Për ta bërë këtë, ne përdorim formulën e Euler-it
.
Në përputhje me këtë formulë, komponenti kth (2.9) i zgjerimit të sinjalit në serinë Fourier mund të përfaqësohet si më poshtë
; 
. (2.15)
Këtu sasitë dhe janë komplekse dhe përfaqësojnë amplituda komplekse të përbërësve të spektrit. Pastaj seria
Fourier (2.8) duke marrë parasysh (2.14) merr formën e mëposhtme
, (2.16)
, (2.17)
Është e lehtë të verifikohet që zgjerimi (2.16) kryhet në funksionet bazë 
, të cilat janë gjithashtu ortogonale në interval 
, d.m.th.
Shprehja (2.16) është formë komplekse Seria Fourier, e cila shtrihet në frekuenca negative. Sasitë dhe 
, ku do të thotë konjugati kompleks i sasisë, quhen amplituda komplekse spektrit. Sepse është një sasi komplekse, rrjedh nga (2.15) se
dhe 
.
Pastaj grupi përbën amplituda, dhe grupi përbën spektrin fazor të sinjalit.
Në fig. 2.4 tregon diagramin spektral të spektrit të sekuencës së mësipërme të pulseve drejtkëndore, të përfaqësuar nga një seri komplekse Furier
Spektri gjithashtu ka një karakter linear, por ndryshe nga spektri i konsideruar më parë, ai përcaktohet si në rajonin e frekuencave pozitive ashtu edhe në rajonin e frekuencave negative. Meqenëse është një funksion çift i argumentit, diagrami spektral është simetrik rreth zeros.
Bazuar në (2.15), është e mundur të vendoset një korrespondencë midis koeficientëve dhe zgjerimit (2.3). Sepse
dhe 
,
atëherë si rezultat marrim
. (2.18)
Shprehjet (2.5) dhe (2.18) lejojnë gjetjen e vlerave në llogaritjet praktike.
Le të japim një interpretim gjeometrik të formës komplekse të serisë Fourier. Le të zgjedhim komponentin k-të të spektrit të sinjalit. Në formë komplekse, komponenti k-të përshkruhet me formulë
ku dhe përcaktohen me shprehjet (2.15).
Në planin kompleks, secili prej termave në (2.19) përshkruhet si vektorë të gjatësisë 
rrotullohet me një kënd dhe në raport me boshtin real dhe rrotullohet në drejtime të kundërta me frekuencë (Fig. 2.5).
Natyrisht, shuma e këtyre vektorëve jep një vektor të vendosur në boshtin real, gjatësia e të cilit është. Por ky vektor korrespondon me komponentin harmonik
Sa i përket projeksioneve të vektorëve në boshtin imagjinar, këto projeksione kanë gjatësi të barabartë, por kahe të kundërta dhe mblidhen deri në zero. Kjo do të thotë se sinjalet e paraqitura në formë komplekse (2.16) janë në fakt sinjale reale. Me fjalë të tjera, forma komplekse e serisë Fourier është matematikore abstraksioni, i cili është shumë i përshtatshëm për zgjidhjen e një numri problemesh të analizës spektrale. Prandaj, ndonjëherë quhet spektri i përcaktuar nga seria trigonometrike e Furierit spektri fizik, dhe forma komplekse e serisë Fourier është spektri matematik.
Dhe në përfundim, le të shqyrtojmë çështjen e energjisë dhe shpërndarjes së energjisë në spektrin e një sinjali periodik. Për këtë përdorim barazinë e Parsevalit (1.42). Kur sinjali zgjerohet në një seri Furier trigonometrike, shprehja (1.42) merr formën
.
Energji konstante
,
dhe energjia e kth harmonike
.
Pastaj energjia e sinjalit
. (2.20)
Sepse fuqia mesatare e sinjalit
,
atëherë duke pasur parasysh (2.18)
. (2.21)
Kur sinjali zgjerohet në një seri komplekse Furier, shprehja (1.42) ka formën
,
ku 
është energjia e kth harmonikës.
Energjia e sinjalit në këtë rast
,
dhe fuqia mesatare e saj
.
Nga shprehjet e mësipërme rezulton se energjia ose fuqia mesatare e komponentit spektral k-të të spektrit matematikor është gjysma e energjisë ose fuqisë së komponentit spektral përkatës të spektrit fizik. Kjo është për shkak të faktit se spektri fizik është i ndarë në mënyrë të barabartë midis dhe spektrit matematik.
| -τ dhe / 2 |
| τ dhe / 2 |
| T |
| t |
| U 0 |
| S (t) |
Detyra numër 1, grupi RI - 210701
Paraqitja spektrale e funksioneve kohore përdoret gjerësisht në teorinë e komunikimit. Për studime teorike dhe eksperimentale të karakteristikave të qarqeve elektrike dhe transmetimit të mesazheve përmes kanaleve të komunikimit, përdoren lloje të ndryshme sinjalesh: lëkundjet harmonike, nivelet e tensioneve konstante, sekuencat e pulseve drejtkëndëshe dhe radio, etj. Sinjalet llogaritëse në formën e një Një funksion i vetëm luan një rol veçanërisht të rëndësishëm në studimet teorike të qarqeve elektrike dhe funksioni i impulsit (funksioni Dirac). Le të përcaktojmë spektrat e sinjaleve tipike më të zakonshme.
11.1 Spektri i një treni me valë katrore
Le të ketë një sekuencë periodike pulsesh drejtkëndëshe me një periodë T, një kohëzgjatje impulsi t dhe një amplitudë A. Shprehja analitike për funksionin që përshkruan një impuls në një segment ka formën
(11.1)
Një grafik i një treni periodik pulsi është paraqitur në figurën 11.1.
Figura 11.1
Ky funksion është çift, pasi grafiku i tij është simetrik në lidhje me boshtin e ordinatave. Më pas koeficientët Furier të këtyre funksioneve llogariten me formula (KFT2), ku.
Numri paraqet vlerën mesatare të funksionit gjatë periudhës dhe quhet komponent konstant. Frekuenca quhet harmonike themelore ose e parë, dhe frekuencat k janë harmonikat më të larta, ku k = 2,3,4, ...
Le të ndërtojmë spektrin e amplitudës së sekuencës së konsideruar të pulseve drejtkëndore. Meqenëse funksioni është periodik, spektri i amplitudës së tij është linear. Le të shënojmë me distancën midis çdo harmonike fqinje. Është e qartë se është e barabartë. Amplituda e kth harmonikës sipas (11.2) ka formën
(11.3)
Le të gjejmë raportin midis periudhës T dhe kohëzgjatjes së pulsit në të cilën amplituda e kth harmonik zhduket.
А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6.36В, А 6 ≈10.5В, А 7 ≈6.36В, А 8 ≈0, А 9 ≈4.95В, А 63 ≈7.
Spektri i amplitudës që rezulton është paraqitur në figurën 11.2.
Figura 11.2
Një spektër i tillë quhet linjë ose spektër diskret.
Spektrat për q = 8 dhe q = 16 janë llogaritur dhe ndërtuar në mënyrë të ngjashme. Ato janë paraqitur përkatësisht në figurat 11.3 dhe 11.4.
Figura 11.3
Figura 11.4
Nga figura mund të shihet se sa më i madh të jetë cikli i funksionimit të pulseve drejtkëndëshe, aq më pak vlerë ka amplituda e harmonikës së parë, por aq më ngadalë zbehet spektri.
11.2 Spektri i një impulsi të vetëm drejtkëndor
Le të shqyrtojmë Ф (11.1) për rastin kur Т → ∞, domethënë, një sekuencë periodike pulsesh degjeneron në një puls të vetëm drejtkëndor me kohëzgjatje t u.
Një shprehje analitike për këtë impuls do të shkruhet si:
Grafiku i këtij funksioni është paraqitur në figurën 11.5.
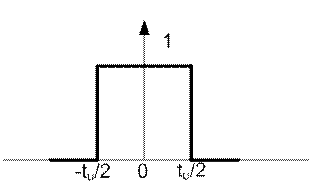
Figura 11.5
Në këtë rast, frekuenca e harmonikës së parë dhe distanca midis harmonikave bëhen të barabarta me 0, prandaj, spektri kthehet nga diskret në një të vazhdueshëm, i përbërë nga një numër pafundësisht i madh linjash spektrale të vendosura në distanca pafundësisht të vogla nga njëra-tjetra. . Një spektër i tillë quhet i vazhdueshëm. Prandaj ndjek rregulli më i rëndësishëm: sinjalet periodike gjenerojnë spektra diskrete, dhe ato jo periodike - të vazhdueshme (të vazhdueshme).
Spektri i një impulsi të vetëm drejtkëndor mund të gjendet direkt nga transformimi i drejtpërdrejtë i Furierit (10.1)