on the topic: Related and vertical angles, their properties.
(3 lessons)
As a result of studying the topic, you need:
BE ABLE TO:Concepts: adjacent and vertical angles, perpendicular lines
Distinguish between adjacent and vertical angles
Theorems of adjacent and vertical angles
Solve problems using properties of adjacent and vertical corners
Adjacent and Vertical Corner Properties
Construct adjacent and vertical angles perpendicular to lines
LITERATURE:
1. Geometry. 7th grade. Zh. Kaidasov, G. Dosmagambetova, V. Abdiev. Almaty "Mektep". 2012
2. Geometry. 7th grade. K.O. Bukubaeva, A.T. Mirazov. AlmatyAtamura". 2012
3. Geometry. 7th grade. Methodological guide. K.O. Bukubaeva. AlmatyAtamura". 2012
4. Geometry. 7th grade. didactic material. A.N.Shynybekov. AlmatyAtamura". 2012
5. Geometry. 7th grade. Collection of tasks and exercises. K.O. Bukubaeva, A.T. Mirazova. AlmatyAtamura". 2012
Remember that you need to work according to the algorithm!
Do not forget to pass the test, make notes in the margins,
Please don't leave any questions you have unanswered.
Be objective during the peer review, it will help both you and the one
who are you checking.
WISH YOU SUCCESS!
TASK №1.
Read the definition and learn (2b):
Definition. Angles that have one side in common and the other two sides are additional rays are called adjacent.
2) Learn and write down the theorem in your notebook: (2b)
Sum adjacent corners equals 180.
Given:∠ ANM and∠ DOV - given adjacent angles
OD - common side
Prove:
∠ AOD+∠ DOV = 180
Proof:

Based on the axiomIII 4:
∠ AOD+∠ DOV =∠ AOW.
∠ AOV - deployed. Consequently,
∠ AOD+∠ DOV = 180
The theorem has been proven.
3) It follows from the theorem: (2b)
1) If two angles are equal, then the angles adjacent to them are equal;
2) if adjacent angles are equal, then degree measure each of them is equal to 90°.
Remember!
An angle equal to 90° is called a right angle.
An angle less than 90° is called an acute angle.
An angle greater than 90° and less than 180° is called an obtuse angle.

Right angle Acute angle Obtuse angle
Since the sum of adjacent angles is 180°, then
1) an angle adjacent to a right angle, right;
2) the angle adjacent to the acute angle is obtuse;
3) an angle adjacent to an obtuse angle is acute.
4) Consider a sample solution hadachi:
a) Given:∠ hkAnd∠ kl- adjacent;∠ hkmore∠ klat 50°.
To find:∠ hkAnd∠ kl.

Solution: Let∠ kl= x, then∠ hk= x + 50°. By property about the sum of adjacent angles∠ kl + ∠ hk= 180°.
x + x + 50° = 180°;
2x = 180° - 50°;
2x = 130°;
x = 65°.
∠ kl= 65°;∠ hk= 65°+ 50° = 115°.
Answer: 115° and 65°.
b) Let∠ kl= x, then∠ hk= 3x
x + 3x = 180°; 4x = 180°; x = 45°;∠ kl= 45°;∠ hk= 135°.
Answer: 135° and 45°.
5) Work with the definition of adjacent corners: (2 b)
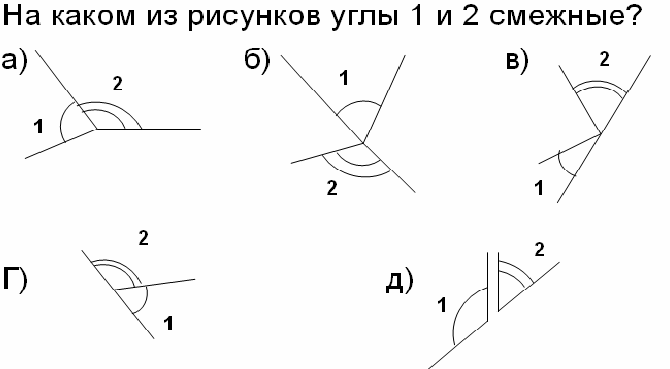
6) Find errors in the definitions: (2b)

Pass test #1
Task number 2
1) Construct 2 adjacent angles so that their common side passes through point C and the side of one of the angles coincides with the ray AB. (2b)
2). Practical work to discover the properties of adjacent corners: (5b)
Working process
1. Build an angleadjacent cornerbut , ifbut : sharp, straight, obtuse.
2. Measure the angles.
3. Enter the measurement data in the table.
4. Find the ratio between the values of the anglesbut And.
5. Draw a conclusion about the property of adjacent angles.
Pass test #2
Task number 3
Draw unexpanded∠ AOB and name the rays that are the sides of this angle.
Draw beam O, which is a continuation of beam OA, and beam OD, which is a continuation of beam OB.
Write in your notebook: angles∠ AOB and∠ SOD are called vertical. (3b)
Learn and write in a notebook: (4b)
Definition: Angles whose sides of one of them are complementary rays of the other are calledvertical corners.

< 1 and<2, <3 и <4 vertical angles
RaysOFAndOA , OCAndOEare pairwise complementary rays.
Theorem: Vertical angles are equal.
Proof.

Vertical angles are formed when two lines intersect. Let the lines a andbintersect at point O.∠ 1 and∠ 2 - vertical angles.
∠ AOC-deployed means∠ AOC= 180°. but∠ 1+ ∠ 2= ∠ AOC, i.e.
∠ 3+ ∠ 1= 180°, hence we have:
∠ 1= 180 - ∠ 3. (1)
We also have that∠ DOV= 180°, hence∠ 2+ ∠ 3= 180° or∠ 2= 180°- ∠ 3. (2)
Since in equalities (1) and (2) the direct parts are equal, then∠ 1= ∠ 2.
The theorem has been proven.
five). Work with the definition of vertical angles: (2b)

6) Find an error in the definition: (2b).

Pass test #3
Task number 4
1) Practical work on discovering the properties of vertical angles: (5b)
Working process:
1. Construct an angle β vertical angleα , ifα :
sharp, straight, obtuse.
2. Measure the angles.
3. Enter the measurement data in the table
4. Find the relationship between the values of the angles α and β.
5. Make a conclusion about the property of vertical angles.
2) Proof of properties of adjacent and vertical angles. (3b)
2) Consider a sample solutionhell.
A task. Lines AB and CD intersect at point O so that∠ AOD = 35°. Find the angles AOC and BOC.

Solution:
1) Angles AOD and AOC are adjacent, therefore∠ BOC= 180° - 35° = 145°.
2) Angles AOC and BOC are also adjacent, therefore∠ BOC= 180° - 145° = 35°.
Means,∠ BOC = ∠ AOD = 35°, and these angles are vertical. Question: Is it true that all vertical angles are equal?
3) Solving problems on finished drawings: (3b)
1. Find the angles AOB, AOD, COD.


3) Find the angles BOC, FOA.: (3b)

3. Find adjacent and vertical angles in the figure. Let the values of the two angles marked on the drawing be known, 28? and 90?. Is it possible to find the values of the remaining angles without taking measurements (2b)
Pass test #4
Task number 5
Test your knowledge by completingverification work No. 1
Task number 6
1) Prove the properties of vertical angles on your own and write down these proofs in a notebook. (3b)
Students independently, using the properties of vertical and adjacent angles, must substantiate the fact that if at the intersection of two lines one of the formed angles is a right one, then the other angles are also right.
2) Solve two problems to choose from:
1. Degree measures of adjacent angles are related as 7:2. Find these angles. (2b)
2. One of the angles formed at the intersection of two lines is 11 times smaller than the other. Find each of the angles. (3b)
3. Find adjacent angles if their difference and their sum are related as 2: 9. (3b)
Task number 7
Well done! You can proceed to test work number 2.
Verification work No. 1.
Decide on the choice of any of the options (10b)
Option 1
<1 и <2,<3 и <2,
G)<1 и <3. Какие это углы?
Related
e) Draw (by eye) an angle of 30 ° and< ABC, adjacent to the given

f) What are the vertical angles?
Two angles are called vertical if the orni are equal.
g) From point A draw two lines perpendicular to the linebut
Only one straight line can be drawn.

Option 2
1. The student, answering the questions of the teacher, gave the appropriate answers. Check if they are correct by marking in the third column with the words "YES", "NO", "I DON'T KNOW". If “NO”, write down the correct answer there or add the missing one.
<1 и <4,<2 и <4
D)<1 и < 3 смежные?
No. They are vertical
E) Which lines are called perpendicular?
Two lines are called perpendicular if they intersect at a right angle.
G) Draw the vertical angles so that their sides are perpendicular lines.

2. Name the vertical angles in this figure.

Total: 10 points
"5" -10 points;
"4" -8-9 points;
"3" -5-7 points.
Verification work No. 2.
Decide on any option
Option I
Find adjacent angles if their difference and their sum are in ratio 2:9. (4b)
Find all non-expanded angles formed at the intersection of two lines, if one of them is 240 ° less than the sum of the other two. (6b)
Option II
1) Find adjacent angles if their difference and their sum are related as 5:8(4b)
2) Find all non-expanded angles formed at the intersection of two lines, if one of them is 60 ° greater than the sum of the other two. (6b)
Total: 10 points
"5" -10 points;
"4" -8-9 points;
"3" -5-7 points.
Geometry is a very multifaceted science. It develops logic, imagination and intelligence. Of course, due to its complexity and the huge number of theorems and axioms, schoolchildren do not always like it. In addition, there is a need to constantly prove their conclusions using generally accepted standards and rules.
Adjacent and vertical angles are an integral part of geometry. Surely many schoolchildren simply adore them for the reason that their properties are clear and easy to prove.
Formation of corners
Any angle is formed by the intersection of two lines or by drawing two rays from one point. They can be called either one letter or three, which successively designate the points of construction of the corner.
Angles are measured in degrees and can (depending on their value) be called differently. So, there is a right angle, acute, obtuse and deployed. Each of the names corresponds to a certain degree measure or its interval.

An acute angle is an angle whose measure does not exceed 90 degrees.
An obtuse angle is an angle greater than 90 degrees.
An angle is called right when its measure is 90.
In the case when it is formed by one continuous straight line, and its degree measure is 180, it is called deployed.
Angles that have a common side, the second side of which continues each other, are called adjacent. They can be either sharp or blunt. The intersection of the line forms adjacent angles. Their properties are as follows:
- The sum of such angles will be equal to 180 degrees (there is a theorem proving this). Therefore, one of them can be easily calculated if the other is known.
- It follows from the first point that adjacent angles cannot be formed by two obtuse or two acute angles.
Thanks to these properties, one can always calculate the degree measure of an angle given the value of another angle, or at least the ratio between them.

Vertical angles
Angles whose sides are continuations of each other are called vertical. Any of their varieties can act as such a pair. Vertical angles are always equal to each other.
They are formed when lines intersect. Together with them, adjacent corners are always present. An angle can be both adjacent for one and vertical for the other.
When crossing an arbitrary line, several more types of angles are also considered. Such a line is called a secant, and it forms the corresponding, one-sided and cross-lying angles. They are equal to each other. They can be viewed in light of the properties that vertical and adjacent angles have.
Thus, the topic of corners seems to be quite simple and understandable. All their properties are easy to remember and prove. Solving problems is not difficult as long as the angles correspond to a numerical value. Already further, when the study of sin and cos begins, you will have to memorize many complex formulas, their conclusions and consequences. Until then, you can just enjoy easy puzzles in which you need to find adjacent corners.
Equal to two right angles .
Given two adjacent angles: AOB And WOS. It is required to prove that:
∠AOW+∠BOS=d+ d = 2d
Let's restore from the point ABOUT to a straight line AC perpendicular OD. We have divided the angle AOB into two parts AOD and DOB so that we can write:
∠AOB = ∠ AOD+∠ DOB
Let us add to both sides of this equality by the same angle BOC, why the equality will not be violated:
∠ AOB + ∠ BOFROM= ∠ AOD + ∠ DOB + ∠ BOFROM
Since the amount DOB + BOC is right angle DOFROM, then
∠ AOB+ ∠ BOFROM= ∠ AOD + ∠ DOFROM= d + d = 2 d,
Q.E.D.
Consequences.
1. Sum of angles (AOb,BOC, COD, DOE) located around a common vertex (O) on one side of the straight line ( AE) is equal to 2 d= 180 0 , because this sum is the sum of two adjacent corners, such as: AOC + COE
2. Sum of angles located around a common peaks (O) on both sides of a straight line is equal to 4 d=360 0 ,
Inverse theorem.
If sum of two angles, having a common vertex and a common side and not covering each other, is equal to two right angles (2d), then such angles - related, i.e. the other two sides are straight line.
If from one point (O) of a straight line (AB) we restore perpendiculars to it, on each of its sides, then these perpendiculars form one straight line (CD). From any point outside the line, you can drop to this line perpendicular and only one.
Because sum of angles COB And BOD is equal to 2d.
StraightFROM parts of which OFROM And OD are perpendicular to the line AB, is called a line perpendicular to AB.
If straight FROMD perpendicular to the line AB, and vice versa: AB perpendicular to FROMD because parts OA And OB serve also perpendicular to FROMD. Therefore, direct AB And FROMD called mutually perpendicular.
That two straight AB And FROMD mutually perpendicular, expressed in writing as AB^ FROMD.
The two corners are called vertical if the sides of one are a continuation of the sides of the other.
Thus, when two lines intersect AB And FROMD two pairs of vertical angles are formed: AOD And COB; AOC And DOB .
Theorem.
Two vertical angle equal .
Let two vertical angles be given: AOD And FROMOB those. OB there is a sequel OA, but OFROM continuation OD.
It is required to prove that AOD = FROMOB.
According to the property of adjacent angles, we can write:
AOD + DOB= 2 d
DOB + BOC = 2d
Means: AOD + DOB = DOB + BOC.
If you subtract from both parts of this equality by angle DOB, we get:
AOD = BOC, which was to be proved.
In a similar way, we will prove that AOC = DOB.
In this lesson, we will consider and understand for ourselves the concept of adjacent angles. Consider the theorem that concerns them. Let's introduce the concept of "vertical angles". Consider the supporting facts concerning these angles. Next, we formulate and prove two corollaries about the angle between the bisectors of vertical angles. At the end of the lesson, we will consider several problems devoted to this topic.
Let's start our lesson with the concept of "adjacent corners". Figure 1 shows the developed angle ∠AOC and the ray OB, which divides this angle into 2 angles.
Rice. 1. Angle ∠AOC
Consider the angles ∠AOB and ∠BOC. It is quite obvious that they have a common side VO, while the sides AO and OS are opposite. Rays OA and OS complement each other, which means they lie on the same straight line. The angles ∠AOB and ∠BOC are adjacent.
Definition: If two angles have a common side, and the other two sides are complementary rays, then these angles are called related.
Theorem 1: The sum of adjacent angles is 180 o.

Rice. 2. Drawing for Theorem 1
∠MOL + ∠LON = 180o. This statement is true because the ray OL divides the straight angle ∠MON into two adjacent angles. That is, we do not know the degree measures of any of the adjacent angles, but we only know their sum - 180 o.
Consider the intersection of two lines. The figure shows the intersection of two lines at point O.

Rice. 3. Vertical angles ∠BOA and ∠COD
Definition: If the sides of one angle are a continuation of the second angle, then such angles are called vertical. That is why the figure shows two pairs of vertical angles: ∠AOB and ∠COD, as well as ∠AOD and ∠BOC.
Theorem 2: Vertical angles are equal.
Let's use Figure 3. Let's consider the developed angle ∠AOC. ∠AOB \u003d ∠AOC - ∠BOC \u003d 180 o - β. Consider the developed angle ∠BOD. ∠COD = ∠BOD - ∠BOC = 180 o - β.
From these considerations, we conclude that ∠AOB = ∠COD = α. Similarly, ∠AOD = ∠BOC = β.
Corollary 1: The angle between the bisectors of adjacent angles is 90°.

Rice. 4. Drawing for consequence 1
Since OL is the bisector of the angle ∠BOA, then the angle ∠LOB = , similarly to ∠BOK = . ∠LOK = ∠LOB + ∠BOK = + = ![]() . The sum of the angles α + β is equal to 180 o, since these angles are adjacent.
. The sum of the angles α + β is equal to 180 o, since these angles are adjacent.
Corollary 2: The angle between the bisectors of the vertical angles is 180°.

Rice. 5. Drawing for consequence 2
KO is the bisector of ∠AOB, LO is the bisector of ∠COD. Obviously, ∠KOL = ∠KOB + ∠BOC + ∠COL = o . The sum of the angles α + β is equal to 180 o, since these angles are adjacent.
Let's consider some tasks:
Find the angle adjacent to ∠AOC if ∠AOC = 111 o.
Let's make a drawing for the task:

Rice. 6. Drawing for example 1
Since ∠AOC = β and ∠COD = α are adjacent angles, then α + β = 180 o. That is, 111 o + β \u003d 180 o.
Hence, β = 69 o.
This type of problem exploits the adjacent angle sum theorem.
One of the adjacent angles is a right angle, which (acute, obtuse or right) is the other angle?
If one of the angles is right and the sum of the two angles is 180°, then the other angle is also right. This task tests knowledge about the sum of adjacent angles.
Is it true that if adjacent angles are equal, then they are right angles?
Let's make an equation: α + β = 180 o, but since α = β, then β + β = 180 o, which means β = 90 o.
Answer: Yes, the statement is true.
Given two equal angles. Is it true that the angles adjacent to them will also be equal?

Rice. 7. Drawing for example 4
If two angles are equal to α, then their corresponding adjacent angles will be 180 o - α. That is, they will be equal to each other.
Answer: The statement is true.
- Alexandrov A.D., Werner A.L., Ryzhik V.I. etc. Geometry 7. - M.: Enlightenment.
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. et al. Geometry 7. 5th ed. - M.: Enlightenment.
- \Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometry 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, edited by V.A. Sadovnichy. - M.: Education, 2010.
- Measurement of segments ().
- General lesson on geometry in the 7th grade ().
- Straight line, segment ().
- No. 13, 14. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometry 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, edited by V.A. Sadovnichy. - M.: Education, 2010.
- Find two adjacent angles if one of them is 4 times the other.
- Given an angle. Build adjacent and vertical angles for it. How many such corners can be built?
- * In what case are more pairs of vertical angles obtained: when three lines intersect at one point or at three points?
CHAPTER I.
BASIC CONCEPTS.
§eleven. ADJACENT AND VERTICAL ANGLES.
1. Adjacent corners.
If we continue the side of some corner beyond its vertex, we will get two corners (Fig. 72): / A sun and / SVD, in which one side BC is common, and the other two AB and BD form a straight line.
Two angles that have one side in common and the other two form a straight line are called adjacent angles.
Adjacent angles can also be obtained in this way: if we draw a ray from some point on a straight line (not lying on a given straight line), then we get adjacent angles.
For example, /
ADF and /
FDВ - adjacent corners (Fig. 73).
Adjacent corners can have a wide variety of positions (Fig. 74).

Adjacent angles add up to a straight angle, so the umma of two adjacent angles is 2d.
Hence, a right angle can be defined as an angle equal to its adjacent angle.
Knowing the value of one of the adjacent angles, we can find the value of the other adjacent angle.
For example, if one of the adjacent angles is 3/5 d, then the second angle will be equal to:
2d- 3 / 5 d= l 2 / 5 d.
2. Vertical angles.
If we extend the sides of an angle beyond its vertex, we get vertical angles. In drawing 75, the angles EOF and AOC are vertical; angles AOE and COF are also vertical.
Two angles are called vertical if the sides of one angle are extensions of the sides of the other angle.

Let be / 1 = 7 / 8 d(Fig. 76). Adjacent to it / 2 will equal 2 d- 7 / 8 d, i.e. 1 1/8 d.
In the same way, you can calculate what are equal to /
3 and /
4.
/
3 = 2d - 1 1 / 8 d = 7 / 8 d; /
4 = 2d - 7 / 8 d = 1 1 / 8 d(Fig. 77).

We see that / 1 = / 3 and / 2 = / 4.
You can solve several more of the same problems, and each time you get the same result: the vertical angles are equal to each other.
However, to make sure that the vertical angles are always equal to each other, it is not enough to consider individual numerical examples, since conclusions drawn from particular examples can sometimes be erroneous.
It is necessary to verify the validity of the property of vertical angles by reasoning, by proof.
The proof can be carried out as follows (Fig. 78):
/
a +/
c = 2d;
/
b +/
c = 2d;
(since the sum of adjacent angles is 2 d).
/ a +/ c = / b +/ c
(since the left side of this equality is equal to 2 d, and its right side is also equal to 2 d).
This equality includes the same angle from.
If we subtract equally from equal values, then it will remain equally. The result will be: / a = / b, i.e., the vertical angles are equal to each other.
When considering the question of vertical angles, we first explained which angles are called vertical, i.e., we gave definition vertical corners.
Then we made a judgment (statement) about the equality of vertical angles and we were convinced of the validity of this judgment by proof. Such judgments, the validity of which must be proved, are called theorems. Thus, in this section we have given the definition of vertical angles, and also stated and proved a theorem about their property.
In the future, when studying geometry, we will constantly have to meet with definitions and proofs of theorems.
3. The sum of angles that have a common vertex.
On the drawing 79 /
1, /
2, /
3 and /
4 are located on the same side of a straight line and have a common vertex on this straight line. In sum, these angles make up a straight angle, i.e.
/
1+ /
2+/
3+ /
4 = 2d.

On the drawing 80 / 1, / 2, / 3, / 4 and / 5 have a common top. In sum, these angles make up a full angle, i.e. / 1 + / 2 + / 3 + / 4 + / 5 = 4d.
Exercises.
1. One of the adjacent angles is 0.72 d. Calculate the angle formed by the bisectors of these adjacent angles.
2. Prove that the bisectors of two adjacent angles form a right angle.
3. Prove that if two angles are equal, then their adjacent angles are also equal.
4. How many pairs of adjacent corners are in drawing 81?

5. Can a pair of adjacent angles consist of two acute angles? from two obtuse corners? from right and obtuse angles? from a right and acute angle?
6. If one of the adjacent angles is right, then what can be said about the value of the angle adjacent to it?
7. If at the intersection of two straight lines there is one right angle, then what can be said about the size of the other three angles?
