El cambio de una función en un punto determinado y se define como el límite del incremento de la función al incremento del argumento, que tiende a cero. Para encontrarlo, usa la tabla de derivadas. Por ejemplo, la derivada de la función y = x3 será igual a y’ = x2.
Iguale esta derivada a cero (en este caso x2=0).
Encuentra el valor de la variable dada. Estos serán los valores cuando esta derivada será igual a 0. Para hacer esto, sustituya números arbitrarios en la expresión en lugar de x, en los que toda la expresión se convertirá en cero. Por ejemplo:
2-2x2=0
(1-x)(1+x) = 0
x1=1, x2=-1
Aplicar los valores obtenidos sobre la recta de coordenadas y calcular el signo de la derivada para cada uno de los obtenidos. Los puntos se marcan en la línea de coordenadas, que se toman como origen. Para calcular el valor en los intervalos, sustituya valores arbitrarios que coincidan con los criterios. Por ejemplo, para la función anterior hasta el intervalo -1, puede elegir el valor -2. Para -1 a 1, puede elegir 0, y para valores mayores que 1, elija 2. Sustituya estos números en la derivada y encuentre el signo de la derivada. En este caso, la derivada con x = -2 será igual a -0,24, es decir negativo y habrá un signo menos en este intervalo. Si x=0, entonces el valor será igual a 2, y se pone un signo en este intervalo. Si x=1, entonces la derivada también será igual a -0.24 y se pone un menos.
Si al pasar por un punto de la línea de coordenadas, la derivada cambia de signo de menos a más, entonces este es un punto mínimo, y si de más a menos, entonces este es un punto máximo.
Videos relacionados
Para encontrar la derivada, existen servicios en línea que calculan los valores requeridos y muestran el resultado. En dichos sitios, puede encontrar un derivado de hasta 5 pedidos.
Fuentes:
- Uno de los servicios para el cálculo de derivados
- punto máximo de la función
Los puntos máximos de la función junto con los puntos mínimos se denominan puntos extremos. En estos puntos, la función cambia su comportamiento. Los extremos se determinan en intervalos numéricos limitados y siempre son locales.
Instrucción
El proceso de encontrar extremos locales se llama función y se realiza analizando las derivadas primera y segunda de la función. Antes de comenzar la exploración, asegúrese de que el rango especificado de valores de argumentos pertenezca a valores permitidos. Por ejemplo, para la función F=1/x, el valor del argumento x=0 no es válido. O para la función Y=tg(x), el argumento no puede tener el valor x=90°.
Asegúrese de que la función Y sea diferenciable en todo el intervalo dado. Encuentre la primera derivada Y". Es obvio que antes de llegar al punto de un máximo local, la función crece, y al pasar por el máximo, la función se vuelve decreciente. La primera derivada en su significado físico caracteriza la tasa de cambio de la función.Mientras la función aumenta, la tasa de este proceso es un valor positivo.Al pasar por un máximo local, la función comienza a disminuir, y la tasa del proceso de cambio de la función se vuelve negativa.La transición de la tasa de cambio de la función a través de cero se produce en el punto del máximo local.
$E \subconjunto \mathbb(R)^(n)$. Se dice que $f$ tiene máximo local en el punto $x_(0) \in E$ si existe una vecindad $U$ del punto $x_(0)$ tal que para todo $x \in U$ la desigualdad $f\left(x\right) \leqslant f \left(x_(0)\right)$.
El máximo local se llama estricto , si la vecindad $U$ se puede elegir de tal manera que para todo $x \in U$ diferente de $x_(0)$ haya $f\left(x\right)< f\left(x_{0}\right)$.
Definición
Sea $f$ una función real en un conjunto abierto $E \subset \mathbb(R)^(n)$. Se dice que $f$ tiene mínimo local en el punto $x_(0) \in E$ si existe una vecindad $U$ del punto $x_(0)$ tal que para todo $x \in U$ la desigualdad $f\left(x\right) \geqslant f \left(x_(0)\right)$.
Se dice que un mínimo local es estricto si la vecindad $U$ puede elegirse de modo que para todo $x \in U$ diferente de $x_(0)$ $f\left(x\right) > f\left(x_ ( 0)\derecha)$.
Un extremo local combina los conceptos de mínimo local y máximo local.
Teorema (condición necesaria para el extremo de una función diferenciable)
Sea $f$ una función real en un conjunto abierto $E \subset \mathbb(R)^(n)$. Si en el punto $x_(0) \in E$ la función $f$ tiene un extremo local también en este punto, entonces $$\text(d)f\left(x_(0)\right)=0. $$ Igualdad a cero diferencial es equivalente al hecho de que todos son iguales a cero, es decir $$\displaystyle\frac(\parcial f)(\parcial x_(i))\left(x_(0)\right)=0.$$
En el caso unidimensional, esto es . Denota $\phi \left(t\right) = f \left(x_(0)+th\right)$, donde $h$ es un vector arbitrario. La función $\phi$ se define para valores de módulo suficientemente pequeños de $t$. Además, con respecto a , es diferenciable, y $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Sea $f$ un máximo local en x $0$. Por lo tanto, la función $\phi$ en $t = 0$ tiene un máximo local y, por el teorema de Fermat, $(\phi)' \left(0\right)=0$.
Entonces, obtuvimos que $df \left(x_(0)\right) = 0$, es decir funciones $f$ en el punto $x_(0)$ cero en cualquier vector $h$.
Definición
Los puntos en los que el diferencial es igual a cero, es decir aquellas en las que todas las derivadas parciales son iguales a cero se llaman estacionarias. puntos críticos Las funciones $f$ son aquellos puntos en los que $f$ no es diferenciable, o es igual a cero. Si el punto es estacionario, entonces todavía no se sigue que la función tenga un extremo en este punto.
Ejemplo 1
Sea $f \left(x,y\right)=x^(3)+y^(3)$. Entonces $\displaystyle\frac(\parcial f)(\parcial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\parcial f)(\parcial y) = 3 \cdot y^(2 )$, entonces $\left(0,0\right)$ es un punto estacionario, pero la función no tiene un extremo en este punto. De hecho, $f \left(0,0\right) = 0$, pero es fácil ver que en cualquier vecindad del punto $\left(0,0\right)$ la función toma valores tanto positivos como negativos.
Ejemplo 2
La función $f \left(x,y\right) = x^(2) − y^(2)$ tiene el origen de coordenadas como un punto estacionario, pero es claro que no hay un extremo en este punto.
Teorema (condición suficiente para un extremo).
Sea una función $f$ diferenciable dos veces continuamente en un conjunto abierto $E \subset \mathbb(R)^(n)$. Sea $x_(0) \in E$ un punto estacionario y $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\parcial^(2) f)(\parcial x_(i) \parcial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Entonces
- si $Q_(x_(0))$ – , entonces la función $f$ en el punto $x_(0)$ tiene un extremo local, a saber, el mínimo si la forma es definida positiva y el máximo si la forma es negativo-definido;
- si la forma cuadrática $Q_(x_(0))$ es indefinida, entonces la función $f$ en el punto $x_(0)$ no tiene extremo.
Usemos la expansión según la fórmula de Taylor (12.7 p. 292) . Teniendo en cuenta que las derivadas parciales de primer orden en el punto $x_(0)$ son iguales a cero, obtenemos $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0) )\derecha) = \frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\parcial^(2) f)(\parcial x_(i) \ parcial x_(j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ donde $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$, y $\epsilon \left(h\right) \rightarrow 0$ para $h \rightarrow 0$, entonces el lado derecho es positivo para cualquier vector $h$ de longitud suficientemente pequeña.
Por lo tanto, hemos llegado a la conclusión de que en alguna vecindad del punto $x_(0)$ la desigualdad $f \left(x\right) >f \left(x_(0)\right)$ se satisface si solo $ x \neq x_ (0)$ (ponemos $x=x_(0)+h$\right). Esto significa que en el punto $x_(0)$ la función tiene un mínimo local estricto, y así queda demostrada la primera parte de nuestro teorema.
Supongamos ahora que $Q_(x_(0))$ es forma indefinida. Entonces hay vectores $h_(1)$, $h_(2)$ tales que $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0$. Entonces obtenemos $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ left[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ Para $t>0$ suficientemente pequeños, el lado derecho es positivo. Esto quiere decir que en cualquier vecindad del punto $x_(0)$ la función $f$ toma valores $f \left(x\right)$ mayores que $f \left(x_(0)\right)$.
De manera similar, obtenemos que en cualquier vecindad del punto $x_(0)$ la función $f$ toma valores menores que $f \left(x_(0)\right)$. Esto, junto con el anterior, hace que la función $f$ no tenga un extremo en el punto $x_(0)$.
Consideremos un caso especial de este teorema para una función $f \left(x,y\right)$ de dos variables definidas en alguna vecindad del punto $\left(x_(0),y_(0)\right) $ y que tiene derivadas parciales continuas de primer y segundo orden. Sea $\left(x_(0),y_(0)\right)$ un punto estacionario y sea $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^( 2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\parcial^(2) f)(\parcial x \parcial y) \left(x_( 0) , y_(0)\right), a_(22)=\frac(\parcial^(2) f)(\parcial y^(2)) \left(x_(0), y_(0)\right ). $$ Entonces el teorema anterior toma la siguiente forma.
Teorema
Sea $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. Luego:
- si $\Delta>0$, entonces la función $f$ tiene un extremo local en el punto $\left(x_(0),y_(0)\right)$, es decir, un mínimo si $a_(11)> 0$ y máximo si $a_(11)<0$;
- si $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.
Ejemplos de resolución de problemas
Algoritmo para encontrar el extremo de una función de muchas variables:
- Encontramos puntos estacionarios;
- Encontramos la diferencial de segundo orden en todos los puntos estacionarios
- Usando una condición suficiente para el extremo de una función de varias variables, consideramos un diferencial de segundo orden en cada punto estacionario
- Investiga la función hasta el extremo $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
SoluciónEncuentre derivadas parciales de primer orden: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) — 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) — 6 \cdot x.$$ Componga y resuelva el sistema: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x ) = 0\\\frac(\f parcial)(\y parcial)= 0\end(casos) \Rightarrow \begin(casos)3 \cdot x^(2) - 6 \cdot y= 0\\24 \ cdot y^(2) - 6 \cdot x = 0\end(cases) \Rightarrow \begin(cases)x^(2) - 2 \cdot y= 0\\4 \cdot y^(2) - x = 0 \end(cases)$$ A partir de la segunda ecuación, expresamos $x=4 \cdot y^(2)$ — sustituimos en la primera ecuación: $$\displaystyle \left(4 \cdot y^(2)\ derecha )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $$ y \left(8 \cdot y^(3) -1\right)=0$$ Como resultado, se obtienen 2 puntos estacionarios:
1) $y=0 \Rightarrow x = 0, M_(1) = \left(0, 0\right)$;
2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \izquierda(\frac(1)(2), 1\derecha)$
Comprobemos el cumplimiento de la condición extrema suficiente:
$$\displaystyle \frac(\parcial^(2) f)(\parcial x^(2))=6 \cdot x; \frac(\parcial^(2) f)(\parcial x \parcial y)=-6; \frac(\parcial^(2) f)(\parcial y^(2))=48 \cdot y$$
1) Para el punto $M_(1)= \left(0,0\right)$:
$$\displaystyle A_(1)=\frac(\parcial^(2) f)(\parcial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\parcial^(2) f)(\parcial x \parcial y) \left(0,0\right)=-6; C_(1)=\frac(\parcial^(2) f)(\parcial y^(2)) \left(0,0\right)=0;$$
$A_(1) \cdot B_(1) - C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Para el punto $M_(2)$:
$$\displaystyle A_(2)=\frac(\parcial^(2) f)(\parcial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\parcial^(2) f)(\parcial x \parcial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\parcial^(2) f)(\parcial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
$A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, entonces hay un extremo en el punto $M_(2)$, y como $A_(2)>0 $, entonces este es el mínimo.
Respuesta: El punto $\displaystyle M_(2) \left(1,\frac(1)(2)\right)$ es el punto mínimo de la función $f$. - Investiga la función para el extremo $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
SoluciónEncuentre puntos estacionarios: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \cdot y + 2 \cdot x — 2.$$
Componga y resuelva el sistema: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases) \ Rightarrow \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(cases) \Rightarrow \begin(cases) y = 2\\y + x = 1\end(casos) \Rightarrow x = -1$$
$M_(0) \left(-1, 2\right)$ es un punto estacionario.
Comprobemos el cumplimiento de la condición extrema suficiente: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0; B=\frac(\parcial^(2) f)(\parcial x \parcial y) \left(-1,2\right)=2; C=\frac(\parcial^(2) f)(\parcial y^(2)) \left(-1,2\right)=2;$$
$A \cdot B - C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Respuesta: no hay extremos.
Límite de tiempo: 0
Navegación (solo números de trabajo)
0 de 4 tareas completadas
Información
Responda este cuestionario para evaluar su conocimiento del tema que acaba de leer, Extremos locales de funciones de muchas variables.
Ya has hecho la prueba antes. No puede volver a ejecutarlo.
La prueba se está cargando...
Debe iniciar sesión o registrarse para comenzar la prueba.
Debes completar las siguientes pruebas para iniciar esta:
resultados
Respuestas correctas: 0 de 4
Su tiempo:
El tiempo se acabo
Obtuviste 0 de 0 puntos (0 )
Tu puntuación se ha registrado en la tabla de clasificación.
- con una respuesta
- Controlado
Tarea 2 de 4
2 .
Número de puntos: 1¿La función $f = 4 + \sqrt((x^(2)+y^(2))^(2))$
Tarea 1 de 4
1 .
Número de puntos: 1Investiga la función $f$ para extremos: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$
Derecha
No está bien
El punto extremo de una función es el punto en el dominio de la función donde el valor de la función toma un valor mínimo o máximo. Los valores de la función en estos puntos se denominan extremos (mínimo y máximo) de la función.
Definición. Punto X1 alcance de la función F(X) se llama punto máximo de la función , si el valor de la función en este punto es mayor que los valores de la función en puntos suficientemente cercanos a ella, situados a la derecha e izquierda de la misma (es decir, la desigualdad F(X0 ) > F(X 0 + Δ X) X1 máximo.
Definición. Punto X2 alcance de la función F(X) se llama punto mínimo de la función, si el valor de la función en este punto es menor que los valores de la función en puntos suficientemente cercanos a ella, situados a la derecha e izquierda de la misma (es decir, la desigualdad F(X0 ) < F(X 0 + Δ X) ). En este caso, se dice que la función tiene en el punto X2 mínimo.
digamos el punto X1 - punto máximo de la función F(X) . Luego en el intervalo hasta X1 aumenta la función, por lo que la derivada de la función es mayor que cero ( F "(X) > 0 ), y en el intervalo posterior a X1 la función es decreciente, entonces derivada de función menos que cero ( F "(X) < 0 ). Тогда в точке X1
Supongamos también que el punto X2 - punto mínimo de la función F(X) . Luego en el intervalo hasta X2 la función es decreciente y la derivada de la función es menor que cero ( F "(X) < 0 ), а в интервале после X2 la función es creciente y la derivada de la función es mayor que cero ( F "(X) > 0 ). En este caso también en el punto X2 la derivada de la función es cero o no existe.
Teorema de Fermat (un criterio necesario para la existencia de un extremo de una función). si el punto X0 - punto extremo de la función F(X), entonces en este punto la derivada de la función es igual a cero ( F "(X) = 0 ) o no existe.
Definición. Los puntos en los que la derivada de una función es igual a cero o no existe se llaman puntos críticos .
Ejemplo 1 Consideremos una función.
En el punto X= 0 la derivada de la función es igual a cero, por lo tanto, el punto X= 0 es el punto crítico. Sin embargo, como se puede ver en la gráfica de la función, crece en todo el dominio de definición, por lo que el punto X= 0 no es un punto extremo de esta función.
Así, las condiciones de que la derivada de una función en un punto sea igual a cero o no exista son condiciones necesarias para un extremo, pero no suficientes, ya que se pueden dar otros ejemplos de funciones para las que se cumplen estas condiciones, pero la función no tiene un extremo en el punto correspondiente. Es por eso debe tener indicaciones suficientes, lo que permite juzgar si hay un extremo en un punto crítico particular y cuál, un máximo o un mínimo.
Teorema (el primer criterio suficiente para la existencia de un extremo de una función). Punto crítico X0 F(X), si la derivada de la función cambia de signo al pasar por este punto, y si el signo cambia de "más" a "menos", entonces el punto máximo, y si de "menos" a "más", entonces el punto mínimo .
Si cerca del punto X0 , a la izquierda y a la derecha de la misma, la derivada conserva su signo, esto significa que la función solo decrece o solo crece en alguna vecindad del punto X0 . En este caso, en el punto X0 no hay extremo.
Entonces, para determinar los puntos extremos de la función, debe hacer lo siguiente :
- Encuentra la derivada de una función.
- Iguale la derivada a cero y determine los puntos críticos.
- Mentalmente o en papel, marque los puntos críticos en el eje numérico y determine los signos de la derivada de la función en los intervalos obtenidos. Si el signo de la derivada cambia de "más" a "menos", entonces el punto crítico es el punto máximo, y si de "menos" a "más", entonces el punto crítico es el punto mínimo.
- Calcular el valor de la función en los puntos extremos.
Ejemplo 2 Encuentra los extremos de una función 
.
Solución. Encontremos la derivada de la función:
Igualar la derivada a cero para encontrar los puntos críticos:
.
Dado que para cualquier valor de "x" el denominador no es igual a cero, igualamos el numerador a cero:
Tengo un punto crítico X= 3 . Determinamos el signo de la derivada en los intervalos delimitados por este punto:
en el rango de menos infinito a 3 - signo menos, es decir, la función disminuye,
en el rango de 3 a más infinito, un signo más, es decir, la función aumenta.
es decir, punto X= 3 es el punto mínimo.
Encuentre el valor de la función en el punto mínimo:
Así, se encuentra el punto extremo de la función: (3; 0) , y es el punto mínimo.
Teorema (el segundo criterio suficiente para la existencia de un extremo de una función). Punto crítico X0 es el punto extremo de la función F(X), si la segunda derivada de la función en este punto no es igual a cero ( F ""(X) ≠ 0 ), además, si la segunda derivada es mayor que cero ( F ""(X) > 0 ), entonces el punto máximo, y si la segunda derivada es menor que cero ( F ""(X) < 0 ), то точкой минимума.
Observación 1. Si en un punto X0 tanto la primera como la segunda derivada desaparecen, entonces en este punto es imposible juzgar la presencia de un extremum sobre la base del segundo signo suficiente. En este caso, debe utilizar el primer criterio suficiente para el extremo de la función.
Observación 2. El segundo criterio suficiente para el extremo de una función tampoco es aplicable cuando la primera derivada no existe en el punto estacionario (entonces tampoco existe la segunda derivada). En este caso, también es necesario utilizar el primer criterio suficiente para el extremo de la función.
La naturaleza local de los extremos de la función.
De las definiciones anteriores se deduce que el extremo de una función tiene un carácter local: este es el valor más grande y más pequeño de la función en comparación con los valores más cercanos.
Suponga que considera sus ganancias en un lapso de tiempo de un año. Si en mayo ganó 45 000 rublos, en abril 42 000 rublos y en junio 39 000 rublos, entonces las ganancias de mayo son la función de ganancias máximas en comparación con los valores más cercanos. Pero en octubre ganó 71 000 rublos, en septiembre 75 000 rublos y en noviembre 74 000 rublos, por lo que las ganancias de octubre son el mínimo de la función de ganancias en comparación con los valores cercanos. Y puede ver fácilmente que el máximo entre los valores de abril-mayo-junio es menor que el mínimo de septiembre-octubre-noviembre.
En términos generales, una función puede tener varios extremos en un intervalo y puede resultar que cualquier mínimo de la función sea mayor que cualquier máximo. Entonces, para la función que se muestra en la figura anterior, .
Es decir, no se debe pensar que el máximo y el mínimo de una función son, respectivamente, sus valores máximo y mínimo en todo el segmento considerado. En el punto máximo, la función tiene el mayor valor solo en comparación con aquellos valores que tiene en todos los puntos suficientemente cerca del punto máximo, y en el punto mínimo, el valor más pequeño solo en comparación con aquellos valores que tiene en todos los puntos suficientemente cerca del punto mínimo.
Por lo tanto, podemos refinar el concepto anterior de puntos extremos de una función y llamar a los puntos mínimos puntos mínimos locales y a los puntos máximos - puntos máximos locales.
Estamos buscando los extremos de la función juntos
Ejemplo 3
Solución La función es definida y continua en la recta numérica entera. su derivado 
también existe en toda la recta numérica. Por lo tanto, en este caso, solo aquellos en los que , es decir, sirven como puntos críticos. , de dónde y . Puntos críticos y dividir todo el dominio de la función en tres intervalos de monotonicidad: . Seleccionamos un punto de control en cada uno de ellos y encontramos el signo de la derivada en este punto.
Para el intervalo, el punto de referencia puede ser: encontramos . Tomando un punto en el intervalo, obtenemos , y tomando un punto en el intervalo, tenemos . Entonces, en los intervalos y , y en el intervalo . Según el primer signo suficiente de un extremo, no hay extremo en el punto (ya que la derivada conserva su signo en el intervalo ), y la función tiene un mínimo en el punto (ya que la derivada cambia de signo de menos a más al pasar por este punto). Encuentre los valores correspondientes de la función: , y . En el intervalo, la función decrece, ya que en este intervalo, y en el intervalo crece, ya que en este intervalo.
Para aclarar la construcción del gráfico, encontramos los puntos de intersección del mismo con los ejes de coordenadas. Cuando obtenemos una ecuación cuyas raíces y , es decir, se encuentran dos puntos (0; 0) y (4; 0) de la gráfica de la función. Usando toda la información recibida, construimos un gráfico (ver al comienzo del ejemplo).
Ejemplo 4 Encuentra los extremos de la función y construye su gráfica.
El dominio de la función es toda la recta numérica, excepto el punto, es decir .
Para acortar el estudio, podemos usar el hecho de que esta función es par, ya que 
. Por lo tanto, su gráfica es simétrica respecto al eje Oye y el estudio solo se puede realizar para el intervalo.
Encontrar la derivada 
y puntos críticos de la función:
1) 
;
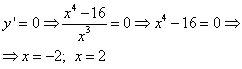2) 
,
pero la función sufre un quiebre en este punto, por lo que no puede ser un punto extremo.
Así, la función dada tiene dos puntos críticos: y . Teniendo en cuenta la paridad de la función, verificamos solo el punto por el segundo signo suficiente del extremo. Para hacer esto, encontramos la segunda derivada 
y determinamos su signo en : obtenemos . Como y , entonces es el punto mínimo de la función, mientras que 
.
Para obtener una imagen más completa de la gráfica de la función, averigüemos su comportamiento en los límites del dominio de definición:
(aquí el símbolo indica el deseo X a cero a la derecha, y X permanece positivo; igualmente significa aspiración X a cero a la izquierda, y X sigue siendo negativo). Así, si , entonces . A continuación, encontramos
,
esos. si, entonces.
La gráfica de la función no tiene puntos de intersección con los ejes. La imagen está al principio del ejemplo.
Seguimos buscando juntos los extremos de la función
Ejemplo 8 Encuentra los extremos de la función.
Solución. Encuentra el dominio de la función. Como la desigualdad debe cumplirse, obtenemos de .
Encontremos la primera derivada de la función:
Encontremos los puntos críticos de la función.
Se dice que la función tiene un punto interno 
áreas D
máximo local(mínimo) si existe tal vecindad del punto 
, para cada punto 
que satisface la desigualdad
Si la función tiene en el punto 
máximo local o mínimo local, entonces decimos que tiene en este punto extremo local(o simplemente extremo).
Teorema
(una condición necesaria para la existencia de un extremum). Si la función diferenciable alcanza un extremo en el punto 
, entonces cada derivada parcial de primer orden de la función 
desaparece en este punto.
Los puntos en los que se anulan todas las derivadas parciales de primer orden se denominan puntos estacionarios de la función
. Las coordenadas de estos puntos se pueden encontrar resolviendo el sistema de 
ecuaciones
.
La condición necesaria para la existencia de un extremo en el caso de una función diferenciable se puede formular brevemente como sigue:
Hay casos en que en determinados puntos algunas derivadas parciales tienen valores infinitos o no existen (mientras que el resto son iguales a cero). Tales puntos se llaman puntos críticos de la función. Estos puntos también deben ser considerados como "sospechosos" para un extremo, al igual que los estacionarios.
En el caso de una función de dos variables, la condición necesaria para un extremo, a saber, la igualdad a cero de las derivadas parciales (diferenciales) en el punto extremo, tiene una interpretación geométrica: plano tangente a la superficie 
en el punto extremo debe ser paralelo al plano 
.
20. Condiciones suficientes para la existencia de un extremum
Ejecución en algún momento condición necesaria la existencia de un extremum no garantiza en absoluto la presencia de un extremum allí. Como ejemplo, podemos tomar la función diferenciable en todas partes 
. Tanto sus derivadas parciales como la función misma se anulan en el punto 
. Sin embargo, en cualquier vecindad de este punto, hay tanto positivos (grandes 
) y negativo (menor 
) valores de esta función. Por lo tanto, en este punto, por definición, no hay extremum. Por tanto, es necesario conocer las condiciones suficientes bajo las cuales un punto sospechoso de un extremo es un punto extremo de la función en estudio.
Consideremos el caso de una función de dos variables. Supongamos que la función 
es definida, continua y tiene derivadas parciales continuas hasta el segundo orden inclusive en una vecindad de algún punto 
, que es el punto estacionario de la función 
, es decir, cumple las condiciones
,
.
Introduzcamos la notación:
Teorema
(condiciones suficientes para la existencia de un extremum). Deja que la función 
satisface las condiciones anteriores, a saber: diferenciable en alguna vecindad del punto estacionario 
y es dos veces diferenciable en el punto mismo 
. Entonces sí
Si 
entonces la función 
en el punto 
alcanza
máximo local en 
Y
mínimo local en 
.
En general, para una función 
condición suficiente para la existencia en un punto 
localmínimo(máximo) es un positivo(negativo) la definición de la segunda diferencial.
En otras palabras, la siguiente afirmación es verdadera.
Teorema
.
Si en el punto 
para la función 
para cualquier no igual a cero al mismo tiempo 
, entonces en este punto la función tiene mínimo(similar máximo, si 
).
Ejemplo 18.Encontrar puntos extremos locales de una función 
Solución. Encuentra las derivadas parciales de la función e igualalas a cero:
Resolviendo este sistema, encontramos dos posibles puntos extremos:
Encontremos las derivadas parciales de segundo orden para esta función:
En el primer punto estacionario , por lo tanto, y 
Por lo tanto, se requiere más investigación para este punto. Valor de función 
en este punto es cero: 
Más,
en 
pero
en 
Por lo tanto, en cualquier vecindad del punto 
función 
toma valores tan grandes 
, y más pequeño 
, y por lo tanto en el punto 
función 
, por definición, no tiene un extremo local.
En el segundo punto estacionario 
por lo tanto, por lo tanto, ya que 
entonces en el punto 
la función tiene un máximo local.