De la definición se deduce que se puede hablar de continuidad solo con respecto a aquellos puntos en los que f(x) está definida (no se estableció tal condición al definir el límite de una función). Para funciones continuas
, es decir, las operaciones f y lim conmutan. De acuerdo con las dos definiciones del límite de una función en un punto, se pueden dar dos definiciones de continuidad: "en el lenguaje de las secuencias" y "en el lenguaje de las desigualdades" (en el lenguaje de ε-δ). Se sugiere que lo haga usted mismo. Para uso práctico a veces es más conveniente definir la continuidad en términos de incrementos.
El valor Δx=x-x 0 se denomina incremento del argumento, y Δy=f(x)-f(x 0) es el incremento de la función al pasar del punto x 0 al punto x.
Definición. Sea f(x) definida en el punto x 0 . La función f(x) se llama continua en el punto x 0 si un incremento infinitesimal del argumento en este punto corresponde a un incremento infinitesimal de la función, es decir, Δy→0 como Δx→0.
Ejemplo 1
Demostrar que la función y=senx es continua para cualquier valor de x.
Solución.
Sea x 0 un punto arbitrario. Dándole un incremento Δx, obtenemos el punto x=x 0 +Δx. Luego 
. Obtenemos 
.
Definición.
La función y=f(x) se llama continua en el punto x 0 a la derecha (izquierda) si
.
Una función continua en un punto interior será continua tanto por la derecha como por la izquierda. Lo contrario también es cierto: si una función es continua en un punto a la izquierda y a la derecha, entonces será continua en ese punto. Sin embargo, la función solo puede ser continua en un lado. por ejemplo, para 
, 
, f(1)=1, por lo tanto, esta función es continua solo por la izquierda (para el gráfico de esta función, consulte la Sección 5.7.2 anterior).
Definición.
Una función se dice continua en algún intervalo si es continua en todos los puntos de este intervalo.
En particular, si el intervalo es un segmento, entonces se implica una continuidad unilateral en sus extremos.
Propiedades de las funciones continuas
1. Todas las funciones elementales son continuas en su dominio de definición.2. Si f(x) y φ(x), dadas en algún intervalo, son continuas en el punto x 0 de este intervalo, entonces las funciones también serán continuas en este punto.
3. Si y=f(x) es continua en un punto x 0 desde X, y z=φ(y) es continua en el punto correspondiente y 0 =f(x 0) desde Y, entonces la función compleja z=φ (f(x )) será continua en el punto x 0 .
Rupturas de función y su clasificación
Un signo de la continuidad de la función f (x) en el punto x 0 es la igualdad, lo que implica la presencia de tres condiciones:1) f(x) está definida en el punto x 0 ;
2)
;
3) .
Si se viola al menos uno de estos requisitos, x 0 se denomina punto de ruptura de la función. En otras palabras, un punto de discontinuidad es un punto donde esta función no es continua. De la definición de puntos de ruptura, se deduce que los puntos de ruptura de una función son:
a) puntos pertenecientes al dominio de la función, en los que f(x) pierde la propiedad de continuidad,
b) puntos que no pertenecen al dominio de f(x), que son puntos adyacentes de dos intervalos del dominio de la función.
Por ejemplo, para una función, el punto x=0 es un punto de quiebre, ya que la función en este punto no está definida y la función
tiene una discontinuidad en el punto x=1, que es adyacente por dos intervalos (-∞,1) y (1,∞) del dominio f(x) y no existe. Se acepta la siguiente clasificación para los puntos de discontinuidad.
1) Si en el punto x 0 hay finitos 
Y 
, pero f(x 0 +0)≠f(x 0 -0), entonces x 0 se llama punto de ruptura del primer tipo
, mientras llaman función de salto
.
Ejemplo 2
Considere la función 
La ruptura de la función solo es posible en el punto x=2 (en otros puntos es continua como cualquier polinomio). 
Encontremos 
, 
. Como los límites unilaterales son finitos, pero no iguales entre sí, en el punto x=2 la función tiene una discontinuidad de primera especie. Darse cuenta de 
, por lo tanto, la función es continua a la derecha en este punto (Fig. 2).
2) Puntos de discontinuidad de segundo tipo.
se denominan puntos en los que al menos uno de los límites unilaterales es igual a ∞ o no existe.
Ejemplo 3
La función y=2 1/ x es continua para todos los valores de x, excepto x=0. Encuentre límites unilaterales: 
, 
, por lo tanto x=0 es un punto de discontinuidad del segundo tipo (Fig. 3).
3) El punto x=x 0 se llama punto de quiebre
, si f(x 0 +0)=f(x 0 -0)≠f(x 0).
La brecha es "removible" en el sentido de que es suficiente cambiar (redefinir o redefinir) el valor de la función en este punto al establecer , y la función se volverá continua en el punto x 0 . 
Ejemplo 4
Se sabe que 
, y este límite no depende de cómo x tiende a cero. Pero la función en el punto x=0 no está definida. Si ampliamos la definición de la función poniendo f(0)=1, entonces resulta ser continua en este punto (en otros puntos es continua como cociente de continuas funciones senx yx). 
Ejemplo 5
Investigar la continuidad de una función 
.
Solución.
Las funciones y=x 3 e y=2x son definidas y continuas en todas partes, incluso en los intervalos indicados. Examinemos el punto de unión de los espacios x=0: 
, 
, . Obtenemos que , de donde se sigue que en el punto x=0 la función es continua.
Definición.
Una función que es continua en un intervalo excepto por un número finito de discontinuidades del primer tipo o una discontinuidad removible se dice que es continua por tramos en este intervalo.
Ejemplos de funciones discontinuas
Ejemplo 1
La función es definida y continua en (-∞,+∞) excepto por el punto x=2. Definamos el tipo de ruptura. En la medida en 
Y 
, entonces en el punto x=2 hay una discontinuidad del segundo tipo (Fig. 6). 
Ejemplo 2
La función es definida y continua para todo x excepto x=0, donde el denominador cero. Encontremos límites laterales en el punto x=0: Los límites unilaterales son finitos y diferentes, por lo tanto, x=0 es un punto de discontinuidad de primera clase (Fig. 7).
Ejemplo 3
Determinar en qué puntos y qué tipo de discontinuidades tiene la función 
Esta función se define en [-2,2]. Dado que x 2 y 1/x son continuas, respectivamente, en los intervalos [-2,0] y , entonces el espacio solo puede estar en la unión de los intervalos, es decir, en el punto x=0. Como , entonces x=0 es un punto de discontinuidad del segundo tipo.
Ejemplo 4
¿Es posible eliminar interrupciones en las funciones?
a) en el punto x=2;
B) 
en el punto x=2;
en) 
en el punto x=1?
Solución.
Sobre el ejemplo a), podemos decir inmediatamente que la discontinuidad f(x) en el punto x=2 no se puede eliminar, ya que en este punto hay infinitos límites unilaterales (ver ejemplo 1).
b) La función g(x) aunque tiene límites unilaterales finitos en el punto x=2
(
,
),
pero no coinciden, por lo que tampoco se puede cerrar la brecha.
c) La función φ(x) en el punto de discontinuidad x=1 tiene límites finitos unilaterales iguales: . Por lo tanto, la brecha se puede eliminar redefiniendo la función en el punto x=1 poniendo f(1)=1 en lugar de f(1)=2.
Ejemplo 5 Demuestre que la función de Dirichlet
discontinua en todos los puntos del eje numérico.
Solución. Sea x 0 cualquier punto desde (-∞,+∞). En cualquiera de sus barrios, hay puntos tanto racionales como irracionales. Esto significa que en cualquier entorno x 0 la función tendrá valores iguales a 0 y 1. En este caso, no puede haber un límite de la función en el punto x 0 ni a la izquierda ni a la derecha, lo que significa que la función de Dirichlet en cada punto del eje real tiene discontinuidades del segundo tipo.
Ejemplo 6 Buscar puntos de ruptura de función
y determinar su tipo.
Solución. Los puntos sospechosos de romperse son puntos x 1 = 2, x 2 = 5, x 3 = 3.
En el punto x 1 =2 f(x) tiene una discontinuidad del segundo tipo, ya que
.
El punto x 2 =5 es un punto de continuidad, ya que el valor de la función en este punto y en sus alrededores está determinado por la segunda línea, no por la primera: .
Exploremos el punto x 3 =3: ,
, de donde se sigue que x=3 es un punto de discontinuidad de primera clase. Por decisión independiente.
Investigue funciones para continuidad y determine el tipo de puntos de discontinuidad:
1) 
; Respuesta: x=-1 – punto de quiebre;
2) 
; Respuesta: Discontinuidad de segunda clase en el punto x=8;
3) 
; Respuesta: Discontinuidad de primera clase en x=1;
4) 
Respuesta: En el punto x 1 \u003d -5 hay un espacio removible, en x 2 \u003d 1 - un espacio de segundo tipo y en el punto x 3 \u003d 0 - un espacio de primer tipo.
5) ¿Cómo se debe elegir el número A para que la función 
sería continua en el punto x=0?
Respuesta: A=2.
6) ¿Es posible elegir el número A para que la función 
sería continua en el punto x=2?
Respuesta: no.
Continuidad de una función en un intervalo
| Nombre del parámetro | Sentido |
| Tema del artículo: | Continuidad de una función en un intervalo |
| Rúbrica (categoría temática) | Matemáticas |
Definición. Una función se dice continua en un intervalo si es continua en todos los puntos de este intervalo.
Si la función está definida para X=pero y donde F(X) = F(pero),
entonces dicen que F(X) en el punto y continua por la derecha. Del mismo modo, si F(X) = F(B), entonces decimos que en el punto B esta función izquierda continua.
Definición. La función se suele llamar continua en el segmento [ a, B], si es continua en cada uno de sus puntos (en el punto pero continua por la derecha, en un punto B es continua por la izquierda).
valor más alto funciones en = F(X) en el segmento [ a, B F(X 1) que F(X) £ F(X 1) para todos X Î [ a, B].
Valor más bajo funciones en = F(X) en el segmento [ a, B] es costumbre llamar a tal su valor F(X 2) que F(X) ³ F(X 2) para todos X Î [ a, B].
Las funciones que son continuas en un intervalo tienen varias propiedades importantes, que se expresan mediante los siguientes teoremas.
Teorema 3.3.1. Una función continua en el segmento [ a, B], alcanza su valor mínimo en él metro y el mayor valor METRO, es decir, hay tales puntos X 1 y X 2 de este segmento, que F(X 1) = metro, F(X 2) = METRO.
El teorema tiene un significado geométrico simple (ver Fig. 2).
 |
Teorema 3.3.2. En caso de que la función en = F(X) es continua en el segmento [ a, B] y toma valores desiguales en sus extremos F(pero) = A, F(B) = B, A ¹ B, entonces cualquiera que sea el número C entre A y B, hay un punto desde Î [ a, B] tal que F(desde) = C.
El significado geométrico del teorema se ilustra en la Fig.3. Cualquier línea recta en= C, donde A< C < B (или A >C > B), corta la gráfica de la función en = F(X).
Consecuencia. Si la función es continua en un segmento y toma valores de diferente signo en sus extremos, entonces hay al menos un punto en ese segmento en el que la función se anula.
El significado geométrico de la consecuencia se ilustra en la Fig.4.
Preguntas para el autocontrol.
1. ¿Qué función se llama continua en un punto?
2. Dar una definición equivalente más a través del incremento de una función y argumentos.
3. ¿Qué se puede decir de la suma, diferencia, producto y cociente de dos funciones continuas?
4. ¿Para qué valores del argumento son continuas las funciones racional entera y racional fraccionaria?
5. ¿Cuándo una función compleja es continua en un punto?
6. ¿Cómo se llama comúnmente el punto de ruptura de las funciones?
7. ¿Qué puntos se llaman puntos de discontinuidad del primer tipo?
8. ¿A qué valor suele llamarse la función salto?
9. Explicar los conceptos de "punto de ruptura removible". Dar ejemplos.
10. ¿Qué puntos se llaman puntos de discontinuidad del segundo tipo? Dar ejemplos.
11. Explicar los conceptos: ""continuidad en el intervalo"", ""continuidad en la derecha"", ""continuidad en la izquierda"", ""continuidad en el segmento"".
12. Definir los valores mayor y menor de las funciones.
13. Formular un teorema sobre la relación de continuidad en un segmento con los valores mayor y menor de la función. Explícalo con una imagen.
14. Formular un teorema sobre la conexión entre la continuidad de funciones en un segmento y el segmento de valores de función. Ilustra su significado geométrico en la figura.
15. Dar una consecuencia del teorema anterior y su interpretación geométrica.
CONFERENCIA №4
Tema de la conferencia: Derivada de función
Plan de lectura: El concepto de derivada, su significado geométrico y físico. Reglas básicas de diferenciación. Derivado función compleja. Algunas aplicaciones de la derivada.
4.1. El concepto de derivada, su significado geométrico y físico
Considere la función en = F(X) especificado en el intervalo ] a, B[. Permitir XÎ ] a, B[ Y X Î ] a, B[, entonces la función se incrementa en el punto X 0 se expresa mediante la fórmula D en = F(X 0+D X) – F(X 0).
Definición. La derivada de la función y = F(X) en el punto X 0 suele llamarse el límite de la razón del incremento de esta función al incremento del argumento cuando este último tiende a cero:
F'(X 0) = 
o y"(X 0) =.
El significado geométrico de la derivada.: la derivada de esta función en un punto es igual a la tangente del ángulo entre el eje Ox y la tangente a la gráfica de esta función en el punto correspondiente (ver Fig. 1):
F"(X 0) = bronceado a.
En esta lección, aprenderemos cómo establecer la continuidad de una función. Haremos esto con la ayuda de límites, además, de un solo lado: derecha e izquierda, que no asustan en absoluto, a pesar de que están escritos como y .
Pero, ¿qué es la continuidad de una función en general? Hasta que lleguemos a una definición estricta, la forma más fácil de imaginar una línea que se pueda dibujar sin levantar el lápiz del papel. Si se dibuja tal línea, entonces es continua. Esta recta es la gráfica de una función continua.
Gráficamente, una función es continua en un punto si su gráfica no se "rompe" en ese punto. La gráfica de tal función continua es 
se muestra en la siguiente figura.
Definición de la continuidad de una función a través del límite. Una función es continua en un punto bajo tres condiciones:
1. La función está definida en el punto .
Si al menos una de las condiciones anteriores no se cumple, la función no es continua en un punto. Al mismo tiempo, dicen que la función sufre un quiebre, y los puntos de la gráfica en los que se interrumpe el gráfico se denominan puntos de quiebre de la función. La gráfica de tal función, que sufre un quiebre en el punto x=2, se muestra en la siguiente figura.
Ejemplo 1 Función F(X) se define de la siguiente manera:
¿Esta función será continua en cada uno de los puntos límite de sus ramas, es decir, en los puntos X = 0 , X = 1 , X = 3 ?
Solución. Verificamos las tres condiciones para la continuidad de la función en cada punto límite. La primera condición se cumple porque función definida en cada uno de los puntos de la frontera se sigue de la definición de la función. Queda por comprobar las dos condiciones restantes.
Punto X= 0 . Encuentre el límite izquierdo en este punto:
.
Encontremos el límite por la derecha:
X= 0 debe encontrarse en la rama de la función que incluye este punto, es decir, la segunda rama. Los encontramos:
Como puede ver, el límite de la función y el valor de la función en el punto X= 0 son iguales. Por tanto, la función es continua en el punto X = 0 .
Punto X= 1 . Encuentre el límite izquierdo en este punto:
Encontremos el límite por la derecha:
Límite de función y valor de función en un punto X= 1 debe encontrarse en la rama de la función que incluye este punto, es decir, la segunda rama. Los encontramos:
.
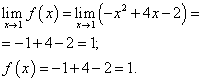Límite de función y valor de función en un punto X= 1 son iguales. Por tanto, la función es continua en el punto X = 1 .
Punto X= 3 . Encuentre el límite izquierdo en este punto:
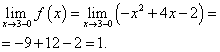
Encontremos el límite por la derecha:
Límite de función y valor de función en un punto X= 3 debe encontrarse en la rama de la función que incluye este punto, es decir, la segunda rama. Los encontramos:
.
Límite de función y valor de función en un punto X= 3 son iguales. Por tanto, la función es continua en el punto X = 3 .
Conclusión principal: esta función es continua en todos los puntos de la frontera.
Establezca usted mismo la continuidad de una función en un punto y luego vea la solución
Un cambio continuo en una función se puede definir como un cambio que es gradual, sin saltos, en el que un pequeño cambio en el argumento conduce a un pequeño cambio en la función.
Ilustremos este cambio continuo de función con un ejemplo.
Deje que una carga cuelgue de un hilo sobre la mesa. Bajo la acción de esta carga, el hilo se estira, por lo que la distancia yo la carga desde el punto de suspensión del hilo es función de la masa de la carga metro, es decir yo = F(metro) , metro≥0 .
Si cambiamos ligeramente la masa de la carga, entonces la distancia yo pequeño cambio: pequeño cambio metro corresponden a pequeños cambios yo. Sin embargo, si la masa de la carga está cerca de la resistencia a la tracción del hilo, entonces un pequeño aumento en la masa de la carga puede hacer que el hilo se rompa: la distancia yo aumentará abruptamente y será igual a la distancia desde el punto de suspensión hasta la superficie de la mesa. Gráfico de función yo = F(metro) se muestra en la figura. En el sitio, este gráfico es una línea continua (sólida), y en el punto se interrumpe. El resultado es un gráfico que consta de dos ramas. En todos los puntos excepto , la función yo = F(metro) es continua, y en un punto tiene una discontinuidad.
El estudio de una función para la continuidad puede ser tanto una tarea independiente como una de las etapas de un estudio completo de la función y la construcción de su gráfico.
Continuidad de una función en un intervalo
Deja que la función y = F(X) definido en el intervalo ] a, B[ y es continua en todos los puntos de este intervalo. Entonces se llama continua en el intervalo ] a, B[ . El concepto de continuidad de una función en intervalos de la forma ]- ∞ se define de manera similar, B[ , ]a, + ∞[ , ]- ∞, + ∞[ . Ahora deja que la función y = F(X) definido en el intervalo [ a, B] . La diferencia entre un intervalo y un segmento es que los puntos límite del intervalo no están incluidos en el intervalo, pero los puntos límite del segmento están incluidos en el segmento. Aquí debemos mencionar la llamada continuidad unilateral: en el punto a, permaneciendo en el intervalo [ a, B] , solo podemos acercarnos desde la derecha, y al punto B- sólo a la izquierda. La función se llama continua en el segmento [ a, B] , si es continua en todos los puntos interiores de este segmento, continua por la derecha en el punto a y continuo a la izquierda en el punto B.
Cualquiera de las funciones elementales puede servir como ejemplo de una función continua. Toda función elemental es continua en cualquier segmento en el que está definida. Por ejemplo, las funciones y son continuas en cualquier intervalo [ a, B] , la función es continua en el intervalo [ 0 , B] , la función es continua en cualquier segmento que no contenga un punto a = 2 .
Ejemplo 4 Investigue la función para la continuidad.
Solución. Verifiquemos la primera condición. La función no está definida en los puntos - 3 y 3. Al menos una de las condiciones para la continuidad de la función en toda la recta numérica no se cumple. Por lo tanto, esta función es continua en los intervalos
.Ejemplo 5 Determine a qué valor del parámetro a continuo a lo largo dominios función 
Solución.
Encontremos el límite de la mano derecha para:
.
Es obvio que el valor en el punto X= 2 debe ser igual hacha :
a = 1,5 .
Ejemplo 6 Determinar a qué valores de los parámetros. a Y B continuo a lo largo dominios función 
Solución.
Encuentre el límite izquierdo de la función en el punto:
.
Por lo tanto, el valor en el punto debe ser igual a 1:
Encontremos la función del lado izquierdo en el punto:
Obviamente, el valor de la función en el punto debe ser igual a:
Respuesta: la función es continua en todo el dominio de definición para a = 1; B = -3 .
Propiedades básicas de las funciones continuas
Las matemáticas llegaron al concepto de función continua estudiando, en primer lugar, varias leyes del movimiento. El espacio y el tiempo son infinitos y la dependencia como caminos s de vez t, expresada por la ley s = F(t) , da un ejemplo de un continuo funciones F(t) . La temperatura del agua calentada también cambia continuamente, también es una función continua del tiempo: T = F(t) .
EN Análisis matemático Se prueban algunas propiedades que poseen las funciones continuas. Presentamos las más importantes de estas propiedades.
1. Si una función que es continua en un intervalo toma valores de diferente signo en los extremos del intervalo, entonces en algún punto de ese segmento toma un valor igual a cero. Más formalmente, esta propiedad se da en un teorema conocido como el primer teorema de Bolzano-Cauchy.
2. Función F(X) , continua en el intervalo [ a, B] , toma todos los valores intermedios entre los valores en los puntos extremos, es decir, entre F(a) Y F(B) . Más formalmente, esta propiedad se da en un teorema conocido como el segundo teorema de Bolzano-Cauchy.
PROPIEDADES DE LAS FUNCIONES CONTINUAS EN UN INTERVALO
Consideremos algunas propiedades de funciones continuas en un intervalo. Presentamos estas propiedades sin demostración.
Función y = f(x) llamado continuo en el segmento [a, B], si es continuo en todos los puntos internos de este segmento, y en sus extremos, es decir en puntos a Y B, es continua por la derecha y por la izquierda, respectivamente.
Teorema 1. Una función continua en el segmento [ a, B], al menos en un punto de este segmento toma el valor más grande y al menos en un punto, el más pequeño.
El teorema establece que si la función y = f(x) continua en el segmento [ a, B], entonces hay al menos un punto x1 Î [ a, B] tal que el valor de la función f(x) en este punto será el mayor de todos sus valores en este segmento: f(x1) ≥ f(x). Del mismo modo, existe tal punto x2, en el que el valor de la función será el menor de todos los valores del segmento: f(x 1) ≤ f(x).
Está claro que puede haber varios de esos puntos, por ejemplo, la figura muestra que la función f(x) toma el valor más pequeño en dos puntos x2 Y X 2 ".
Comentario. El enunciado del teorema puede volverse falso si consideramos el valor de la función en el intervalo ( a, B). En efecto, si consideramos la función y=x en (0, 2), entonces es continua en este intervalo, pero no alcanza sus valores máximos o mínimos en él: alcanza estos valores en los extremos del intervalo, pero los extremos no pertenecen a nuestro región.
Además, el teorema deja de ser cierto para funciones discontinuas. Dar un ejemplo.
Consecuencia. Si la función f(x) continuo en [ a, B], entonces está acotado en este intervalo.
Teorema 2. Deja que la función y = f(x) continua en el segmento [ a, B] y toma valores de diferentes signos en los extremos de este segmento, entonces hay al menos un punto dentro del segmento x=c, donde la función desaparece: f(C)= 0, donde un< C< b
Este teorema tiene un significado geométrico simple: si los puntos de la gráfica de una función continua y = f(x), correspondiente a los extremos del segmento [ a, B] acostarse lados diferentes fuera del eje Buey, entonces esta gráfica al menos en un punto del segmento interseca al eje Buey. Las funciones discontinuas pueden no tener esta propiedad.
Este teorema admite la siguiente generalización.
Teorema 3 (teorema de los valores intermedios). Deja que la función y = f(x) continua en el segmento [ a, B] Y f(a) = A, f(b) = segundo. Entonces para cualquier número C Entre A Y B, hay tal punto dentro de este segmento CÎ [ a, B], qué f(c) = C.
Este teorema es geométricamente obvio. Considere la gráfica de la función y = f(x). Permitir f(a) = A, f(b) = segundo. Entonces cualquier línea y=c, donde C- cualquier número entre A Y B, corta la gráfica de la función al menos en un punto. La abscisa del punto de intersección será ese valor x=c, en el cual f(c) = C.
Así, una función continua, al pasar de uno de sus valores a otro, pasa necesariamente por todos los valores intermedios. En particular:
Consecuencia. Si la función y = f(x) es continua en algún intervalo y toma los valores mayor y menor, luego en este intervalo toma, al menos una vez, cualquier valor entre sus valores menor y mayor.
DERIVADO Y SUS APLICACIONES. DEFINICIÓN DE DERIVADOS
Tengamos alguna función y=f(x), definido en algún intervalo. Para cada valor de argumento X de este intervalo la función y=f(x) tiene un cierto significado.
Considere dos valores de argumento: inicial X 0 y nuevo X.
Diferencia x–x 0 se llama incremento del argumento x en el punto X 0 y denotado Δx. De este modo, ∆x = x – x 0 (el incremento del argumento puede ser positivo o negativo). De esta igualdad se sigue que x=x 0 +Δx, es decir. el valor inicial de la variable ha recibido algún incremento. Entonces, si en el punto X 0 el valor de la función era f(x 0 ), entonces en el nuevo punto X la función tomará el valor f(x) = f(x 0 +∆x).
Diferencia aaa 0 = f(x) – f(x 0 ) llamado incremento de función y = f(x) en el punto X 0 y se denota con el símbolo Δy. De este modo,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
Por lo general, el valor inicial del argumento X 0 se considera fijo y el nuevo valor X- variable. Luego y 0 = f(x 0 ) resulta ser constante y y = f(x)- variable. incrementos Δy Y Δx también serán variables y la fórmula (1) muestra que dy es una función de la variable Δx.
Componga la razón del incremento de la función al incremento del argumento
Encontremos el límite de esta relación en Δx→0. Si este límite existe, entonces se llama la derivada de esta función. f(x) en el punto X 0 y denota F "(X 0). Entonces,
derivado esta función y = f(x) en el punto X 0 se llama el límite de la relación de incremento de la función Δ y al incremento del argumento Δ X cuando este último tiende arbitrariamente a cero.
Tenga en cuenta que para la misma función la derivada en diferentes puntos X puede tomar diferentes valores, es decir la derivada se puede considerar como una función del argumento X. Esta función se denota F "(X)
La derivada se denota con los símbolos F "(x),y", . El valor específico del derivado en x = un denotado F "(a) o y "| x=a.
La operación de hallar la derivada de una función f(x) se llama la diferenciación de esta función.
Para encontrar directamente la derivada por definición, puede aplicar lo siguiente regla de oro:
Ejemplos.
SIGNIFICADO MECÁNICO DE LA DERIVADA
Se sabe por la física que Movimiento uniforme tiene la forma s = v t, donde s- trayectoria recorrida hasta el punto en el tiempo t, v es la velocidad del movimiento uniforme.
Sin embargo, desde la mayoría de los movimientos que ocurren en la naturaleza son desiguales, entonces, en el caso general, la velocidad y, en consecuencia, la distancia s dependerá del tiempo t, es decir. será una función del tiempo.
Entonces, deje que el punto material se mueva en línea recta en una dirección de acuerdo con la ley s=s(t).
Tenga en cuenta un momento en el tiempo t 0 En este punto, el punto ha pasado el camino s=s(t 0 ). Determinemos la velocidad v punto material en el tiempo t 0 .
Para hacer esto, considere algún otro momento en el tiempo t 0 + Δ t. Corresponde a la distancia recorrida s =s(t 0 + Δ t). Entonces para el intervalo de tiempo Δ t el punto ha recorrido el camino Δs =s(t 0 + Δ t)–S t).
Consideremos la relación. Se llama velocidad media en el intervalo de tiempo Δ t. La velocidad promedio no puede caracterizar con precisión la velocidad de movimiento de un punto en el momento t 0 (porque el movimiento es desigual). Para expresar con mayor precisión esta velocidad real usando velocidad media, necesita tomar un intervalo de tiempo más pequeño Δ t.
Entonces, la velocidad de movimiento en un momento dado t 0 (velocidad instantánea) es el límite de la velocidad media en el intervalo desde t 0 a t 0 +Δ t cuando Δ t→0:
,
esos. velocidad de movimiento desigual es la derivada de la distancia recorrida con respecto al tiempo.
SIGNIFICADO GEOMÉTRICO DE LA DERIVADA
Primero introduzcamos la definición de una tangente a una curva en un punto dado.
Tengamos una curva y un punto fijo en ella METRO 0(ver figura) Considere otro punto METRO esta curva y dibujar una secante METRO 0 METRO. si el punto METRO comienza a moverse a lo largo de la curva, y el punto METRO 0 permanece estacionario, la secante cambia de posición. Si con aproximación ilimitada del punto METRO curva a punto METRO 0 en cualquier lado, la secante tiende a tomar la posición de una cierta línea recta L 0 T, entonces la recta L 0 T se llama tangente a la curva en el punto dado METRO 0.
Que., tangente a la curva en un punto dado METRO 0 llamada posición límite de la secante METRO 0 METRO cuando el punto METRO tiende a lo largo de la curva a un punto METRO 0.
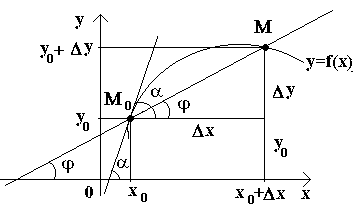
Considere ahora la función continua y=f(x) y la curva correspondiente a esta función. Por algún valor X 0 función toma un valor y0=f(x0). Estos valores X 0 y y 0 en la curva corresponde a un punto M 0 (x 0; y 0). Vamos a dar un argumento x0 incremento Δ X. El nuevo valor del argumento corresponde al valor incrementado de la función y 0 +Δ y=f(x 0 –Δ X). obtenemos un punto M(x 0+Δ X; 0+Δ y). Dibujemos una secante METRO 0 METRO y denotemos por φ el ángulo formado por la secante con la dirección positiva del eje Buey. Hagamos una relación y observemos que .
Si ahora Δ X→0, entonces, debido a la continuidad de la función Δ en→0, y por lo tanto el punto METRO, moviéndose a lo largo de la curva, se acerca indefinidamente al punto METRO 0. Entonces la secante METRO 0 METRO tenderá a tomar la posición de una tangente a la curva en el punto METRO 0, y el ángulo φ→α en Δ X→0, donde α denota el ángulo entre la tangente y la dirección positiva del eje Buey. Como la función tg φ depende continuamente de φ en φ≠π/2, entonces en φ→α tg φ → tg α y, por tanto, la pendiente de la tangente será:
esos. f"(x)= tgα.
Así, geométricamente y "(x 0) representa la pendiente de la tangente a la gráfica de esta función en el punto x0, es decir. en valor dado argumento X, la derivada es igual a la tangente del ángulo formado por la tangente a la gráfica de la función f(x) en el punto correspondiente M 0 (x; y) con sentido de eje positivo Buey.
Ejemplo. Encuentre la pendiente de la tangente a la curva y = x 2 en el punto METRO(-1; 1).
Ya hemos visto que ( X 2)" = 2X. Pero la pendiente de la tangente a la curva es tg α = y"| x=-1 = - 2.
DIFERENCIABILIDAD DE FUNCIONES. CONTINUIDAD DE UNA FUNCIÓN DIFERENCIABLE
Función y=f(x) llamado diferenciable en algún momento X 0 si tiene cierta derivada en este punto, es decir si el límite de la relación existe y es finito.
Si una función es derivable en todos los puntos de algún segmento [ pero; B] o intervalo ( pero; B), entonces dicen que diferenciable en el segmento [ pero; B] o, respectivamente, en el intervalo ( pero; B).
Es válido el siguiente teorema, que establece una conexión entre funciones diferenciables y continuas.
Teorema. Si la función y=f(x) diferenciable en algún punto x0, entonces es continua en este punto.
Así, la derivabilidad de una función implica su continuidad.
Prueba. Si 
, luego
,
donde α es un valor infinitesimal, es decir cantidad que tiende a cero en Δ X→0. Pero entonces
Δ y=F "(x0) Δ X+αΔ X=> Δ y→0 en Δ X→0, es decir f(x) – f(x0)→0 en X→X 0, lo que significa que la función f(x) continuo en el punto X 0 QED
Así, en los puntos de discontinuidad, la función no puede tener derivada. La afirmación inversa no es cierta: hay funciones continuas que no son derivables en algunos puntos (es decir, no tienen derivada en esos puntos).
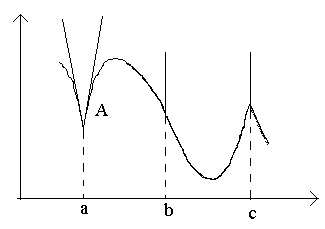
Considere los puntos en la figura a B C.
En el punto a en Δ X→0 la relación no tiene límite (porque los límites unilaterales son diferentes para Δ X→0–0 y Δ X→0+0). En el punto A el gráfico no tiene una tangente definida, pero hay dos tangentes de un lado diferentes con pendientes para 1 y para 2. Este tipo de punto se llama punto de esquina.
En el punto B en Δ X→0 el cociente es de signo constante valor infinitamente grande . La función tiene una derivada infinita. En este punto, la gráfica tiene una tangente vertical. Tipo de punto: "punto de inflexión" con una tangente vertical.
En el punto C Las derivadas unilaterales son cantidades infinitamente grandes de signos diferentes. En este punto, el gráfico tiene dos tangentes verticales fusionadas. Escriba - "cúspide" con una tangente vertical - un caso especial de un punto de esquina.
Definición. Si la función F(X) se define en el intervalo [ un, b], es continua en cada punto del intervalo ( un, b), en el punto a continua por la derecha, en un punto B es continua por la izquierda, entonces decimos que la función F(X) continuo en el segmento [un, b].
En otras palabras, la función F(X) es continua en el segmento [ un, b] si se cumplen tres condiciones:
1) "X 0 Î( un, b): F(X) = F(X 0);
2) F(X) = F(a);
3) F(X) = F(B).
Para funciones que son continuas en un intervalo, consideramos algunas propiedades, que formulamos en la forma de los siguientes teoremas sin demostraciones.
Teorema 1. Si la función F(X) es continua en el segmento [ un, b], luego alcanza su valor más pequeño y más grande en este segmento.
Este teorema establece (Fig. 1.15) que en el segmento [ un, b] hay tal punto X 1 que F(X 1) £ F(X) para cualquier X desde [ un, b] y que hay un punto X 2 (X 2 О[ un, b]) tal que " XÎ[ un, b] (F(X 2) ³ F(X)).
Sentido F(X 1) es el mayor para la función dada en [ un, b], pero F(X 2) - el más pequeño. Denotar: F(X 1) = METRO, F(X 2) =metro. Desde hace F(X) se cumple la siguiente desigualdad: " XÎ[ un, b] metro£ F(X) £ METRO, entonces obtenemos el siguiente corolario del Teorema 1.
Consecuencia. Si la función F(X) es continua en un segmento, entonces está acotada en este segmento.
Teorema 2. Si la función F(X) es continua en el segmento [ a, b] y toma valores de diferentes signos en los extremos del segmento, entonces existe tal punto interior X 0 segmento [ un, b], en el que la función se convierte en 0, es decir PS X 0 Î ( un, b) (F(X 0) = 0).
Este teorema establece que la gráfica de una función y = f(X), continua en el segmento [ un, b], cruza el eje Buey al menos una vez si los valores F(a) Y F(B) tener signos opuestos. Entonces, (Fig. 1.16) F(a) > 0, F(B) < 0 и функция F(X) desaparece en puntos X 1 , X 2 , X 3 .
Teorema 3. Deja que la función F(X) es continua en el segmento [ un, b], F(a) = A, F(B) = B Y A¹ B. (Figura 1.17). Entonces para cualquier número C, concluido entre los números A Y B, hay tal punto interior X 0 segmento [ un, b], qué F(X 0) = C.
Consecuencia. Si la función F(X) es continua en el segmento [ un, b], metro- el valor más pequeño F(X), METRO- el mayor valor de la función F(X) en el segmento [ un, b], entonces la función toma (al menos una vez) cualquier valor metro Entre metro Y METRO, y por lo tanto el segmento [ metro] es el conjunto de todos los valores de la función F(X) en el segmento [ un, b].
Tenga en cuenta que si la función es continua en el intervalo ( un, b) o tiene en el intervalo [ un, b] del punto de discontinuidad, entonces los Teoremas 1, 2, 3 dejan de ser verdaderos para tal función.
En conclusión, considere el teorema sobre la existencia de una función inversa.
Recuerde que un intervalo es un segmento, un intervalo o un semiintervalo finito o infinito.
 |
Teorema 4. Permitir F(X) es continua en el intervalo X, aumenta (o disminuye) en X y tiene un rango de valores Y. Entonces para la función y = f(X) hay una función inversa X= j(y) definido en el intervalo Y, continuo y creciente (o decreciente) en Y con muchos significados X.
Comentario. Deja que la función X= j(y) es inversa para la función F(X). Dado que el argumento generalmente se denota por X, y la función a través de y, luego escribimos función inversa como y=j(X).
Ejemplo 1. Función y=x 2 (Fig. 1.8, a) en el set X= }