"Sinusu un kosinusu teorēma" - 1) Pieraksti šī trijstūra sinusa teorēmu: Atrodi leņķi B. Pieraksti aprēķina formulu: Sinusu teorēma: Atrodi malas BC garumu. Sinusu un kosinusu teorēmas. Trijstūra malas ir proporcionālas pretējo leņķu sinusiem. 2) Pierakstiet kosinusa teorēmu, lai aprēķinātu MK malu: Patstāvīgais darbs:
"Trigonometrisko nevienādību risinājums" - visas y vērtības intervālā MN. 1. Veidojam funkciju grafikus: Citi intervāli. Taisne y=-1/2 krusto sinusoīdu bezgalīgā skaitā punktu, bet trigonometrisko apli punktā A. bezgalīgi daudz atstarpju. Un sinusoīdā vērtību intervāls x, kas ir vistuvāk koordinātu sākumam, pie kura sinx> -1/2,
"Trigonometriskās formulas" — formulas trigonometrisko funkciju summas pārvēršanai reizinājumā. Formulas trigonometrisko funkciju reizinājuma pārvēršanai summā. Papildināšanas formulas. Pēc leņķa trigonometriskajām funkcijām?. Dubultā leņķa formulas. Saskaitot vienādības (3) un (4) pa vārdam, iegūstam: Atvasināsim palīgformulas, kas ļauj atrast.
"Vienkāršāko trigonometrisko nevienādību risinājums" - cos x. Trigonometrisko nevienādību risināšanas metodes. sinx. Trigonometriskās nevienādības sauc par nevienādībām, kas satur mainīgo trigonometriskās funkcijas argumentā. Vienkāršāko trigonometrisko nevienādību risinājums.
"Grēks un cos" - vai tā ir taisnība, ka kosinuss 6,5 ir lielāks par nulli? 60° sinuss ir vienāds ar?? Vai tā ir taisnība, ka cos? x - malks? x=1? Matemātikas sadaļa, kas pēta sinusa, kosinusa īpašības ... Algebras stunda un analīzes sākums 10. klasē. Risinājums trigonometriskie vienādojumi un nevienlīdzības. Vienības apļa punkta abscisa. Kosinusa un sinusa attiecība...
"Kosinusa teorēma trijstūrim" - Mutisks darbs. nezināmi elementi. Trīsstūris. Trijstūra malas kvadrāts. Formulējiet kosinusu teorēmu. Teorēma. Kosinusa teorēma. Problēmu risināšana uz šūnu papīra. stūri un sāni. Formulējiet kosinusu teorēmu. Uzdevumi pēc gataviem rasējumiem. Dati, kas parādīti attēlā.
Kopumā tēmā ir 21 prezentācija
Sinusa grafiks pa vilnim
Abscisa aizbēg.No studentu dziesmas.
NODARBĪBAS MĒRĶI UN UZDEVUMI:
- IZGLĪTĪBAS: formulu atvasināšana sakarībai starp sinusu, kosinusu un tā paša leņķa (skaitļa) tangensu; iemācīties izmantot šīs formulas, lai aprēķinātu skaitļa sinusa, kosinusa, tangensa vērtības, ņemot vērā vienas no tām vērtību.
- ATTĪSTĪBA: iemācīties analizēt, salīdzināt, veidot analoģijas, vispārināt un sistematizēt, pierādīt un atspēkot, definēt un izskaidrot jēdzienus.
- IZGLĪTĪBAS: apzinīgas attieksmes pret darbu un pozitīvas attieksmes pret zināšanām izglītība.
VESELĪBAS GLABĀŠANA: komfortabla psiholoģiskā klimata radīšana klasē, sadarbības atmosfēra: skolēns - skolotājs.
NODARBĪBAS METODOLISKAIS APRĪKOJUMS:
MATERIĀLĀ UN TEHNISKĀ BĀZE: Matemātikas kabinets.
NODARBĪBAS DIDAKTISKS ATBALSTS: mācību grāmata, klade, plakāti par nodarbības tēmu, galdi, dators, diski, ekrāns, projektors.
AKTIVITĀTES METODES: grupu un individuālais darbs pie rakstāmgalda un pie tāfeles.
NODARBĪBAS VEIDS: nodarbība jaunu zināšanu apguvē.
NODARBĪBU LAIKĀ
1. Organizatoriskais brīdis: sasveicināšanās, studentu apmeklējuma pārbaude, žurnāla aizpildīšana.
2. Skolēnu gatavības stundai pārbaude: skolēnu nostādīšana pie darba, stundas plāna atnešana.
3. Mājasdarbu kļūdu analīze. Uz ekrāna - attēls ar pareizi izpildītu mājas darbu. Katrs skolēns pārbauda ar detalizētu frontālo skaidrojumu un atzīmē īstenošanas pareizību nodarbības darba kartītē.
DARBA NODARBĪBAS KARTE.
C / o - pašcieņa.
O / t - drauga novērtējums.
4. Zināšanu aktualizēšana, sagatavošanās jauna materiāla uztverei.
Nākamais mūsu nodarbības posms ir diktēšana. Īsi pierakstām atbildes – zīmējums ir mūsu slaidā.
Dikts (vajadzīgās informācijas mutiska atkārtošana):
1. Definējiet:
- taisnleņķa trijstūra asā leņķa A sinusu;
- taisnleņķa trijstūra asā leņķa B kosinuss;
- taisnleņķa trijstūra asā leņķa A tangensa;
- taisnleņķa trijstūra asā leņķa B kotangenss;
- kādus ierobežojumus mēs uzliekam sinusam un kosinusam, nosakot akūta leņķa tangensu un kotangensu taisnleņķa trīsstūris.
2. Definējiet:
- leņķa sinuss a a.
- leņķa kosinuss a caur punkta koordinātu (ko), kas iegūta, pagriežot punktu (1; 0) ap sākumu par leņķi a.
- leņķa pieskare a.
- leņķa kotangenss a.
3. Pieraksti sinusa, kosinusa, tangensa, kotangensa zīmes leņķiem, kas iegūti, pagriežot punktu P (1; 0) par leņķi.
4. Visiem šiem leņķiem norādiet koordinātu plaknes ceturtdaļas.
Puiši kopā ar skolotāju pārbauda diktātu slaidā, skaidrojot katru apgalvojumu un atzīmējot sevi stundas darba lapā.
5. No trigonometrijas vēstures. Mūsdienu trigonometrijas formu piešķīra lielākais 18. gadsimta matemātiķis Leonards Eilers- Šveices pēc dzimšanas ilgi gadi kurš strādāja Krievijā un bija Sanktpēterburgas Zinātņu akadēmijas biedrs. Viņš iepazīstināja ar labi zināmām trigonometrisko funkciju definīcijām, formulēja un pierādīja reducēšanas formulas, kas jums vēl ir jāatbilst, un atšķirīgās pāra un nepāra funkciju klases.
6. Jauna materiāla ieviešana:
Galvenais ir ne tikai informēt studentus par gala secinājumiem, bet padarīt studentus it kā par zinātniskā meklējuma dalībniekiem: uzdodot jautājumu, lai viņi, pamodinājuši zinātkāri, tiktu iekļauti pētījumā. , kas veicina skolēnu augstāka garīgās attīstības līmeņa sasniegšanu.
Tāpēc, ieviešot jaunu materiālu, es veidoju problēmsituāciju - cik vienkāršāk un racionālāk noteikt sakarību starp viena un tā paša leņķa sinusu un kosinusu - caur vienības riņķa vienādojumu vai caur Pitagora teorēmu.
Klase ir sadalīta variantos pirmajam un otrajam variantam - uz ekrāna ir slaids ar nosacījumu un zīmējumiem, risinājuma vēl nav.
1. variants nosaka attiecības starp sinusu un kosinusu, izmantojot vienādojumu aplim, kura centrs atrodas sākuma punktā un kura rādiuss ir vienāds ar 1x 2 +y 2 =1; sin 2 + cos 2 =1.
2. variants nosaka attiecības starp sinusu un kosinusu, izmantojot Pitagora teorēmu - taisnleņķa trijstūrī hipotenūzas kvadrāts ir vienāds ar kāju kvadrātu summu: OB 2 + AB 2 \u003d OA 2 - un mēs iegūstam grēku. 2 + cos 2 \u003d 1.
Viņi salīdzina rezultātus, izdara secinājumus: galvenais, vai ir izpildīta vienlīdzība attiecībā uz jebkurām tajā iekļauto burtu vērtībām? Studentiem jāatbild, ka tas ir tas pats
(slaidā ir parādīts pareizais risinājums gan pirmajai, gan otrajai opcijai).
Esam ieguvuši vienādību, kas ir spēkā jebkurai tajā ietverto burtu vērtībām. Kā sauc šīs vienlīdzības? Tieši tā – identitātes.
Atgādiniet - kādas vēl identitātes mēs zinām algebrā - saīsinātās reizināšanas formulas:
a 2 -b 2 \u003d (a-b) (a + b),
(a-b) 2 \u003d a 2 -2ab + b 2,
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 2,
(a-b) 3 =a 3 -3a 2 b+3ab 3 -b 3,
a 3 -b 3 \u003d (a-b) (a 2 + ab + b 2),
a 3 + b 3 \u003d (a + b) (a 2 -ab + b 2).
Nākamā problēma - kāpēc mēs atvasinājām galveno trigonometrisko identitāti - sin 2 + cos 2 =1.
Tieši tā - lai atrastu vienu zināmu sinusa, kosinusa vai tangensa vērtību - visu pārējo funkciju vērtības.
Tagad mēs vienmēr varam izmantot pamata trigonometrisko identitāti, bet galvenais ir viens un tas pats arguments.
Iegūto zināšanu pielietojums:
1. IESPĒJA — izsakiet sinusu leņķa kosinusa izteiksmē.
2. iespēja — izteikt kosinusu leņķa sinusa izteiksmē. Pareizā atbilde ir slaidā.
Skolotājas jautājums - neviens nav aizmirsis nolikt + un - zīmes? Kāds varētu būt leņķis? - jebkurš.
No kā šajās formulās zīme saknes priekšā ir atkarīga? kurā ceturtdaļā atrodas mūsu definējamās trigonometriskās funkcijas leņķis (arguments).
Uzstājamies pie tāfeles 2 skolēni Nr.457. - 1. variants - 1, 2. variants - 2.
Slaidā ir parādīta pareizā atbilde.
Patstāvīgs darbs pie trigonometriskās pamatidentitātes atpazīšanas
1. atrodiet izteiksmes vērtību:
2. izsaka skaitli 1 caur leņķi a, ja
Notiek abpusēja pārbaude - pēc gatavā slaida un darba vērtējuma - gan pēc pašvērtējuma, gan pēc drauga vērtējuma.
6. Jauna materiāla konsolidācija (pēc G.E. Hazankina tehnoloģijas - atbalsta uzdevumu tehnoloģija).
1. PROBLĒMA. Aprēķināt ……….. ja ………………………………………………………………….
1 skolēns pie tāfeles patstāvīgi - tad slidiniet ar pareizo risinājumu.
UZDEVUMS 2. Aprēķini……………., ja…………………………………………………………………..
2. skolēns pie tāfeles, tad slidiniet ar pareizo risinājumu.
7. Fiziskās audzināšanas minūte.Es zinu, ka jūs jau esat pieauguši un domājat, ka nemaz neesat noguris, it īpaši tagad, kad stunda ir tik aktīva, ka laiks mums, šķiet, pagarinās - pēc A. Einšteina relativitātes teorijas , bet nodarbosimies ar vingrošanu smadzeņu asinsvadiem:
- pagriežot un noliekot galvu pa labi - pa kreisi, uz augšu - uz leju
- plecu jostas un galvas ādas masāža - rokas no rokas, sejas un pakauša - no augšas uz leju.
- paceliet plecus uz augšu un atpūtieties "nolaidiet" uz leju. Katru vingrinājumu veicam 5-6 reizes!
Tagad noskaidrosim attiecības starp tangensu un kotangensu…………………………………………………………………………………………………… ………
Ir jauns pētījums par tēmu - kāds var būt leņķis otrajā trigonometriskajā identitātē?
GALVENAIS IR PRETOT KOMPLEKTU, UZ KURĀ ŠĪS LĪDZĪBAS TIEK VEIKTAS. ATZĪMĒJIET ATTĒLĒ PUNKTU, KUROS LEŅĶA TANGENTES UN KOTENCENCE NAV.
3. skolēns pie tāfeles. Vienlīdzības ir spēkā ……………………….
UZDEVUMS3. Aprēķināt………, ja………………………….
4. Uzdevums. Aprēķini…………….. ja …………………………………………………………………
Pārējie skolēni strādā savās piezīmju grāmatiņās.
1 ATBALSTS…………………………………………………………………………………………………
2 ATBALSTS…………………………………………………………………………………………………
3 ATBALSTS. Trigonometriskās pamatidentitātes pielietošana problēmu risināšanā.
8. Krustvārdu mīkla. Anatols Frenss reiz teica: "Mācīties vajadzētu būt jautrai... Lai zināšanas sagremotu, tās jāuzņem ar apetīti."
Lai pārbaudītu savas zināšanas par šo tēmu, jums tiek piedāvāta krustvārdu mīkla.
- Matemātikas nozare, kas pēta sinusa, kosinusa, tangensa īpašības ...
- Vienības apļa punkta abscisa.
- Kosinusa un sinusa attiecība.
- Sinuss ir ... .. punkti uz vienības apļa.
- Vienlīdzība, kas neprasa pierādījumus un ir patiesa jebkurai tajā iekļauto burtu vērtībai. To sauc……
Pārbaudījuši krustvārdu mīklu, puiši liek sev atzīmes nodarbības darba kartītē. Skolotājs atzīmē tos skolēnus, kuri stundā ir īpaši aktīvi. Rezultāts - GPA darbam klasē.
9. Uzdot skolotājam pildīt mājasdarbus.
10. Skolotāja rezumējot stundu.
11. Mājasdarbs: 25. rindkopa (pirms 5. uzdevuma), #459 (pāra), 460 (pāra), 463*(4). Mācību grāmata Sh.A Alimov "Algebra un analīzes sākums", 10-11, "Apgaismība", M., 2005.
Temats: Trigonometriskās formulas(25 stundas)
6.–7. nodarbība: Attiecība starp sinusu, kosinusu un tangensu vienā un tajā pašā leņķī.
Mērķis: izpētīt attiecības starp viena un tā paša leņķa sinusu, kosinusu un tangensu. Lai sasniegtu šo mērķi, ir nepieciešams:
- Zināt:
- galveno trigonometrisko funkciju definīciju formulējumi (sinuss, kosinuss un tangenss); trigonometrisko funkciju pazīmes ceturkšņos; trigonometrisko funkciju vērtību kopa; trigonometrijas pamatformulas.
- Saprast:
- ka trigonometrisko pamatidentitāti var izmantot tikai vienam un tam pašam argumentam; algoritms vienas trigonometriskās funkcijas aprēķināšanai, izmantojot citu.
- Pieteikties:
- prasme izvēlēties pareizo formulu konkrēta uzdevuma risināšanai; prasme strādāt ar vienkāršām daļskaitļiem; prasme veikt trigonometrisko izteiksmju transformāciju.
- Analīze:
- analizēt kļūdas argumentācijas loģikā.
- Sintēze:
- piedāvāt savu piemēru risināšanas veidu; izveidot krustvārdu mīklu, izmantojot iegūtās zināšanas.
- Atzīme:
- zināšanas un prasmes par šo tēmu izmantošanai citās algebras sadaļās.
- Laika organizēšana.
- Zināšanu un prasmju atjaunošana.
- Kurā ceturksnī ir 1 radiāna leņķis un ar ko tas ir aptuveni vienāds?
- Kura vārda trūkst sinusa funkcijas definīcijā?
- Kura vārda trūkst kosinusa funkcijas definīcijā?
- Kādas vērtības var uzņemt sinusu?
() - Jaunā materiāla skaidrojums.
uzzīmēsim vienību apli, kura centrs ir punktā O. Iegūsim rādiusu OB, pagriežot rādiusu OA, kas vienāds ar R, pa leņķi (5. att.). Tad pēc definīcijas 
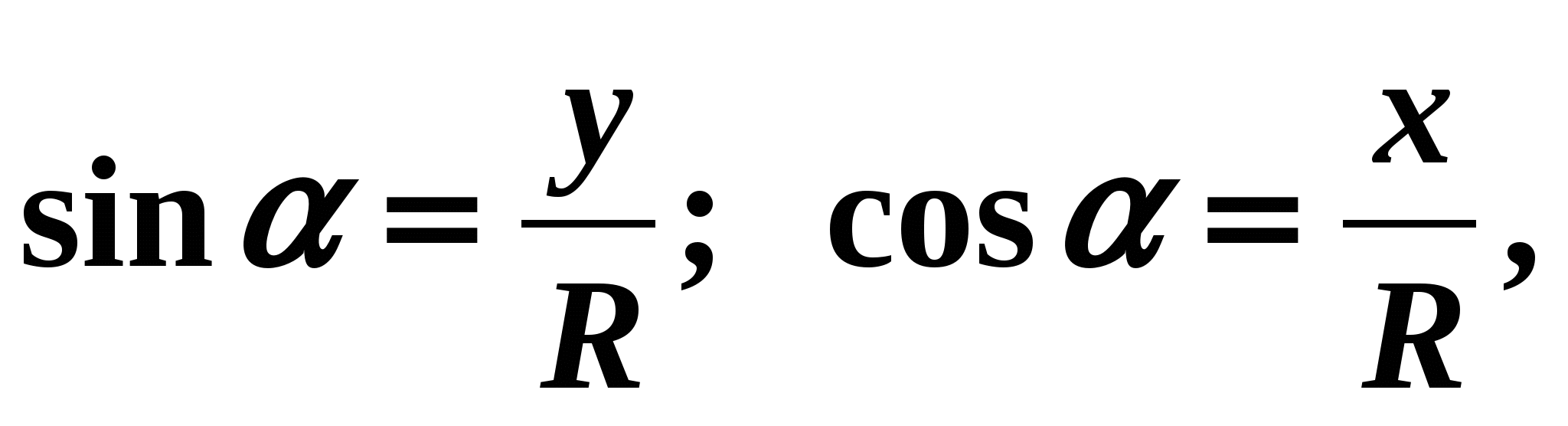kur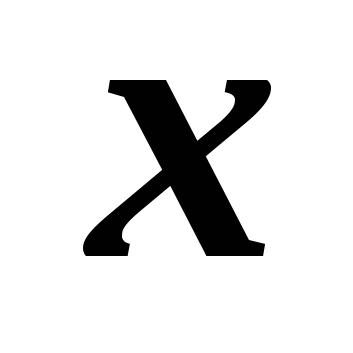 
- punkta B abscisa, 
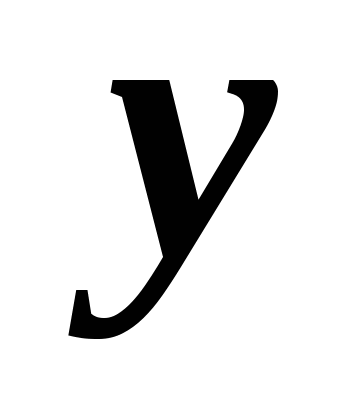ir tā ordināta. No tā izriet, ka punkts B pieder aplim. Tāpēc tā koordinātas apmierina vienādojumu 
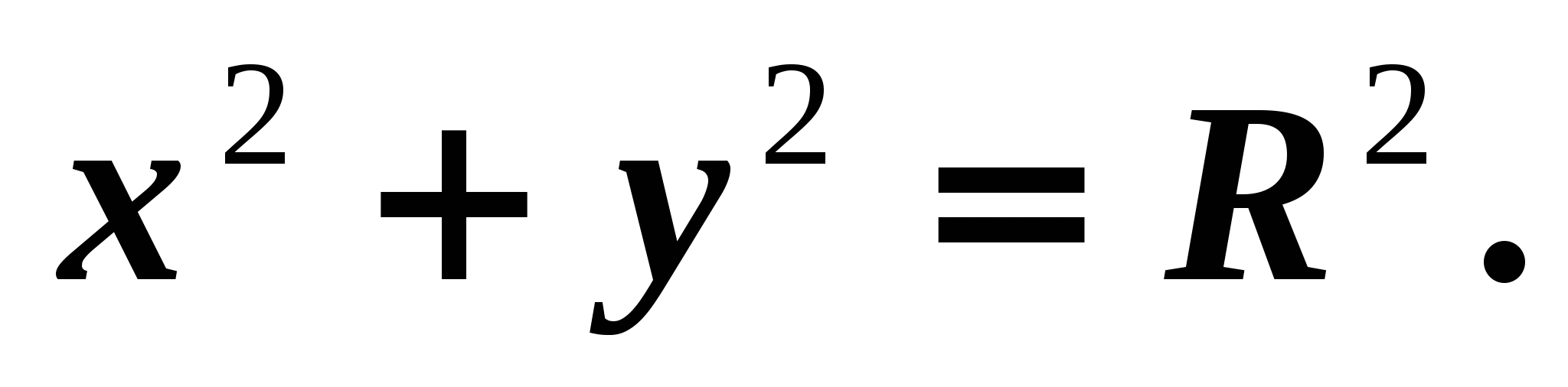Izmantojot to, ko mēs iegūstam 
(1).
Esam ieguvuši vienādību, kas ir spēkā jebkurai tajā ietverto burtu vērtībām. Kā sauc šīs vienlīdzības? Tieši tā – identitātes. Vienādību (1) sauc pamata trigonometriskā identitāte. Vienādībā (1) var pieņemt jebkuras vērtības. Pabeidziet ierakstu pats: 1.
Pārbaudiet, vai jūsu ieraksts ir pareizs. Ievietojiet sev punktus mācību kartītē par Uzdevumi numur 2. Mēs turpinām. Mēs esam atvasinājuši pamata trigonometrisko identitāti, bet kāpēc mums tā ir vajadzīga? Tieši tā – atrast kosinusu no vienas zināmas sinusa vērtības un otrādi. Tagad mēs vienmēr varam izmantot pamata trigonometrisko identitāti, bet galvenais ir viens un tas pats arguments. Skolēni piezīmju grāmatiņā tiek aicināti patstāvīgi no trigonometriskās pamatidentitātes izteikt sinusu caur kosinusu un kosinusu caur sinusu. Divi skolēni tiek izsaukti pie tāfeles pārbaudīt. Viens tiek aicināts izteikt sinusu caur kosinusu, otrs - kosinusu caur sinusu. Pareizā atbilde tiek parādīta ekrānā:
Studenti pārbauda savas atbildes un novērtē stundas kartītē par Uzdevumi numur 3.
No kā šajās formulās ir atkarīga zīme saknes priekšā? (Uz kuras ceturkšņa atrodas mūsu definētās trigonometriskās funkcijas leņķis). 1. piemērs . Aprēķināt
ja 
Nosakiet ceturksni, kurā atrodas leņķis 
. ceturksnis - III. Atgādiniet, ka sinuss trešajā ceturksnī ir negatīvs, t.i., formulā (2) pirms saknes ir jāievieto zīme “-”: 2. piemērs
Aprēķināt 
ja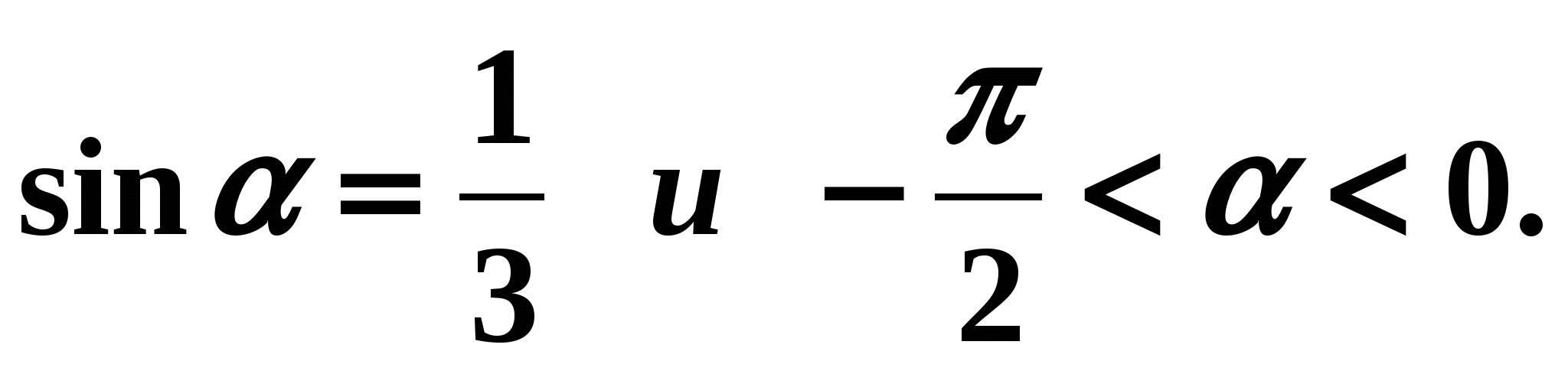 
Nosakām ceturksni, kurā atrodas leņķis . Ceturksnis - IV, kosinuss ceturtajā ceturksnī ir pozitīvs. Tāpēc formulā (3) pirms saknes ir nepieciešama “+” zīme: Uzziniet tūlīt attiecības starp tangensu un kotangensu. Pēc pieskares un kotangensa definīcijas
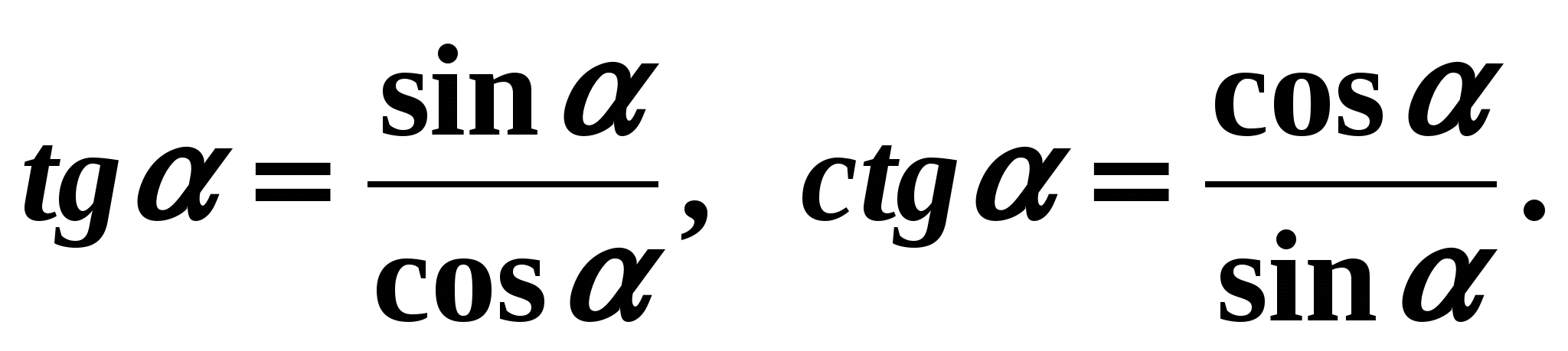
Reizinot šīs vienādības, mēs iegūstam:
No vienlīdzības (4) varam izteikt
pāri 
un otrādi: 
Vienādības (4) - (6) ir patiesas visām vērtībām, kurām
jēga, t.i., kad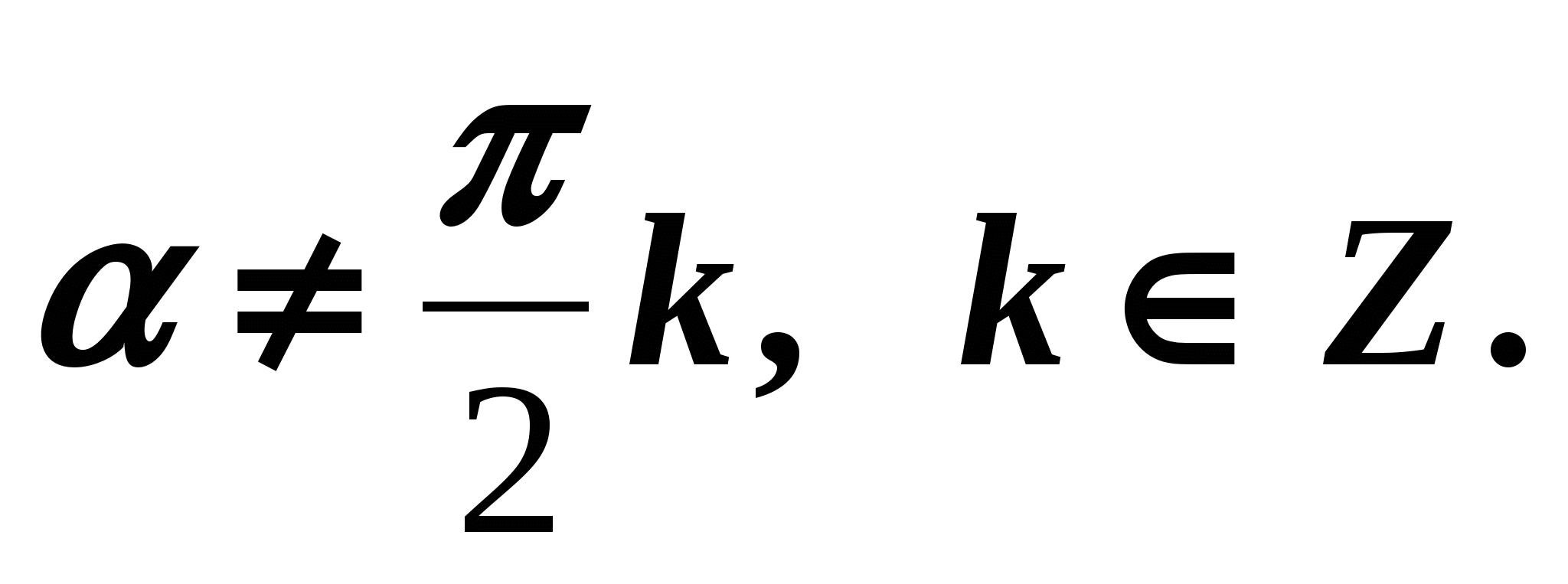 
Tagad mēs iegūstam formulas, kas izsaka attiecības starp tangensu un kosinusu, kā arī kotangensu un sinusu vienam argumentam. Abas vienlīdzības puses (1) dalot ar 
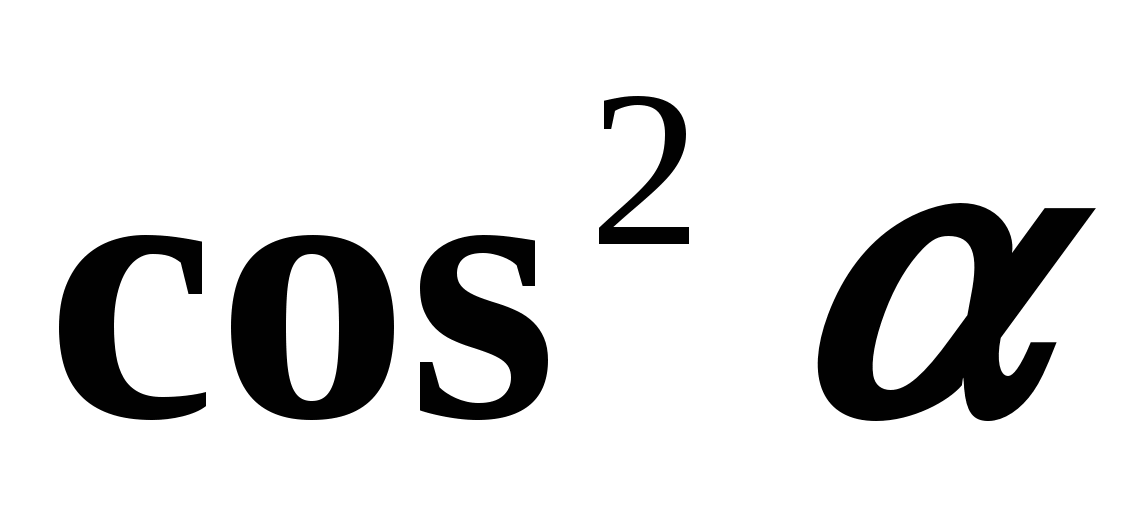, mēs iegūstam: 
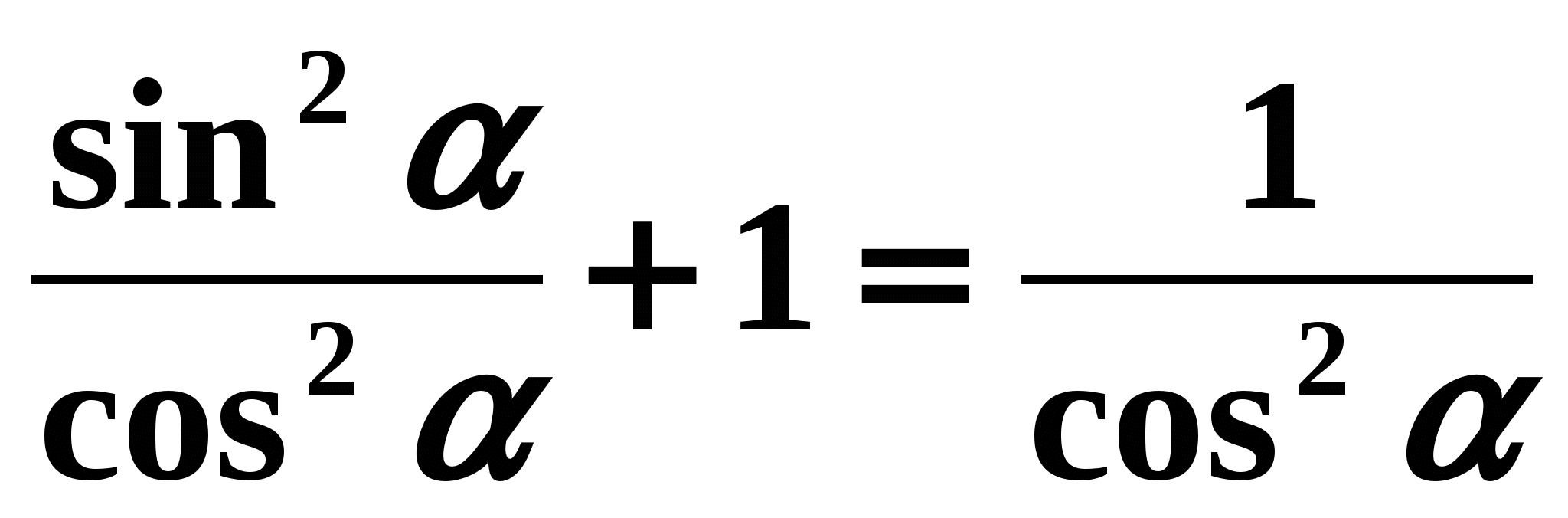tie. 
Ja abas vienādības daļas (1) dala ar
, tad mums būs: 
tie. 
Apsveriet piemērus, kā izmantot atvasinātās formulas, lai atrastu trigonometrisko funkciju vērtības no vienas no zināmās vērtības.
1. piemērs Atrodiet, vai mēs to zinām
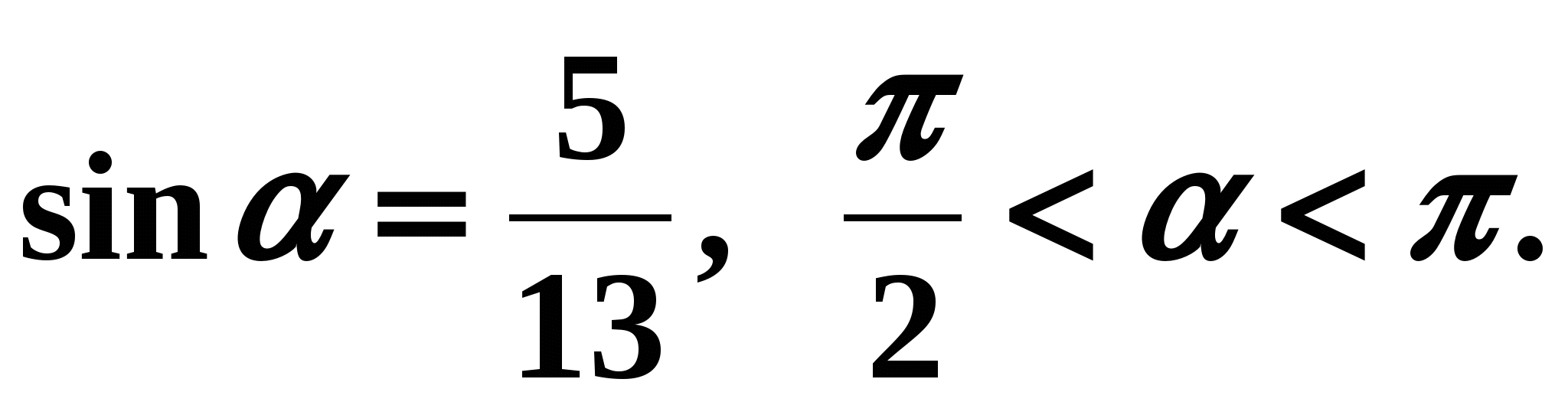Risinājums: 
- Lai atrastu leņķa kotangensu, ir ērti izmantot formulu (6):
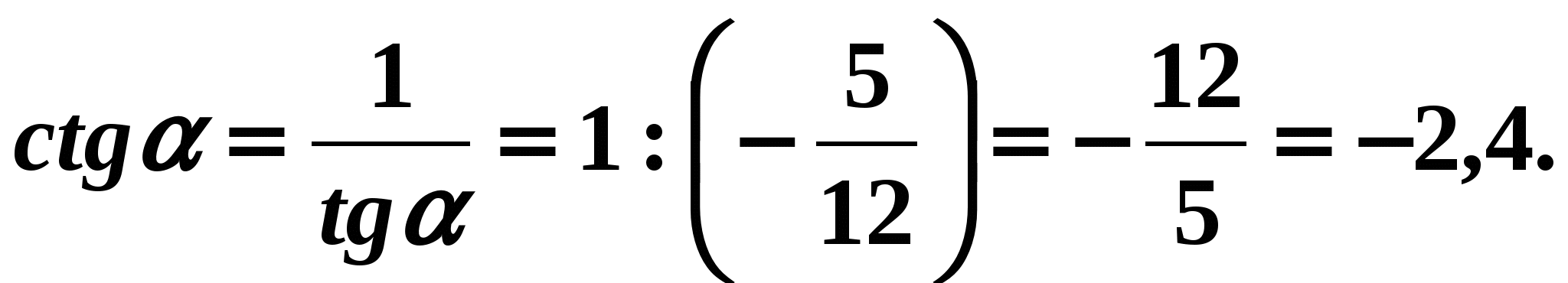Atbilde: Piemērs2. Ir zināms, ka
. Atrodiet visas pārējās trigonometriskās funkcijas. Risinājums: - Izmantosim formulu (7).
Mums ir:
, 
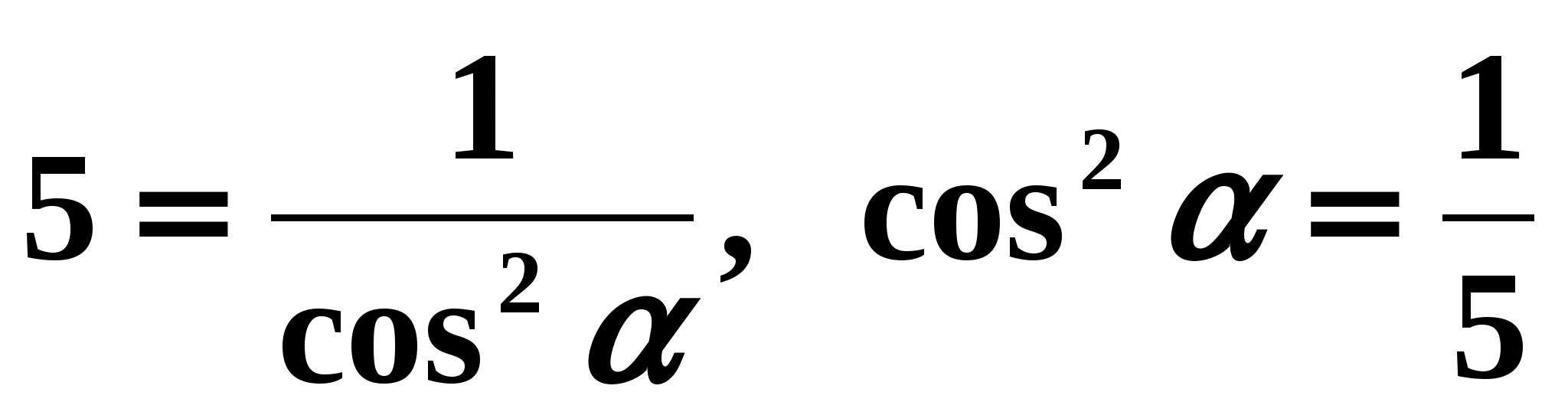. Atbilstoši uzdevuma nosacījumam leņķis ir 1 ceturtdaļas leņķis, tātad tā kosinuss ir pozitīvs. Līdzekļi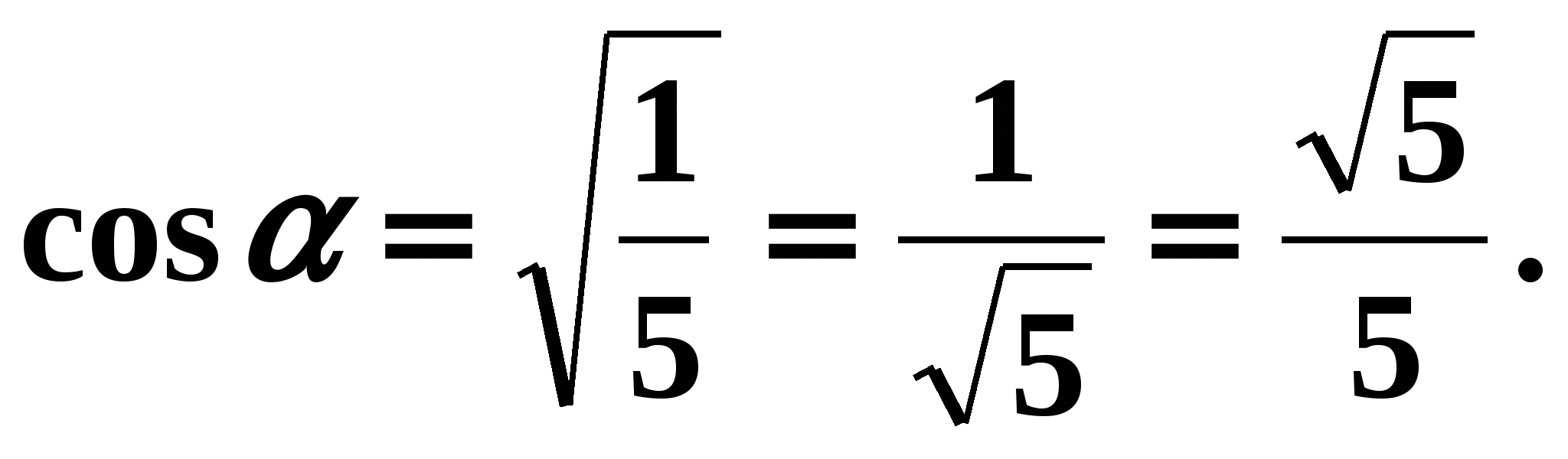 
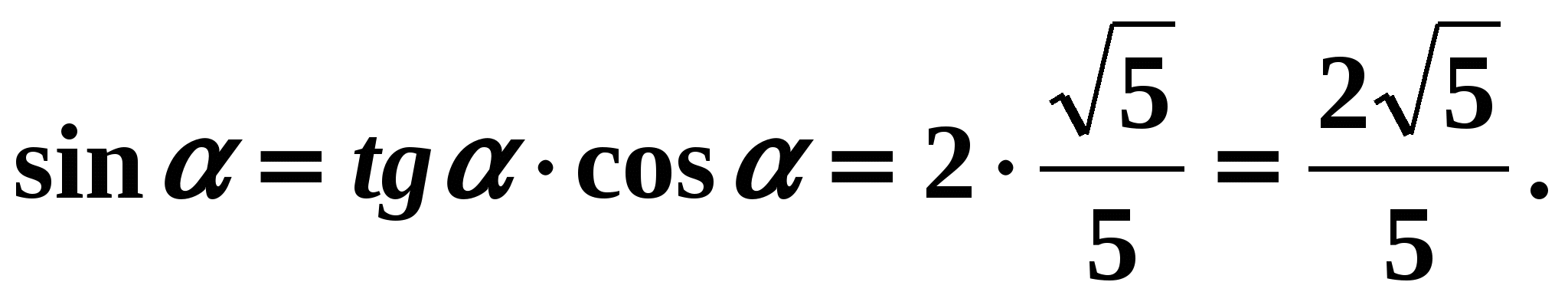
Atbilde:
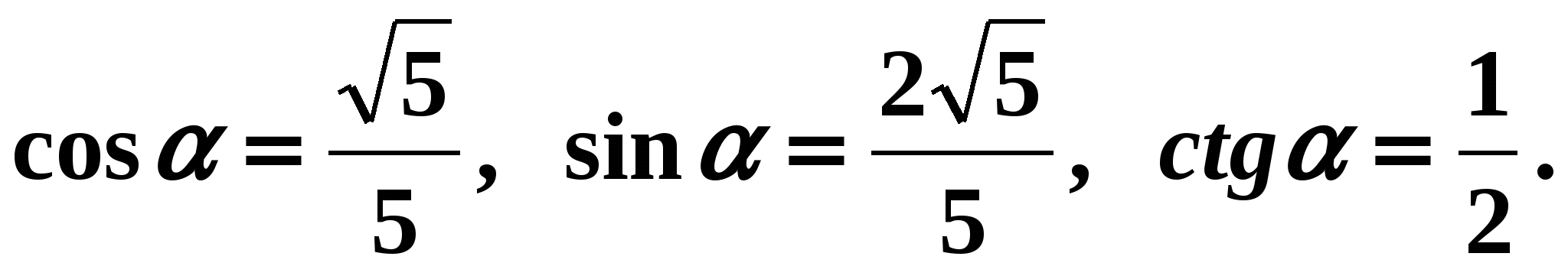Nodibinātas attiecības starp trigonometriskās funkcijas Tas pats arguments ļauj mums vienkāršot trigonometriskās izteiksmes. 3. piemērs Vienkāršosim izteicienu:
Risinājums: Izmantosim formulas: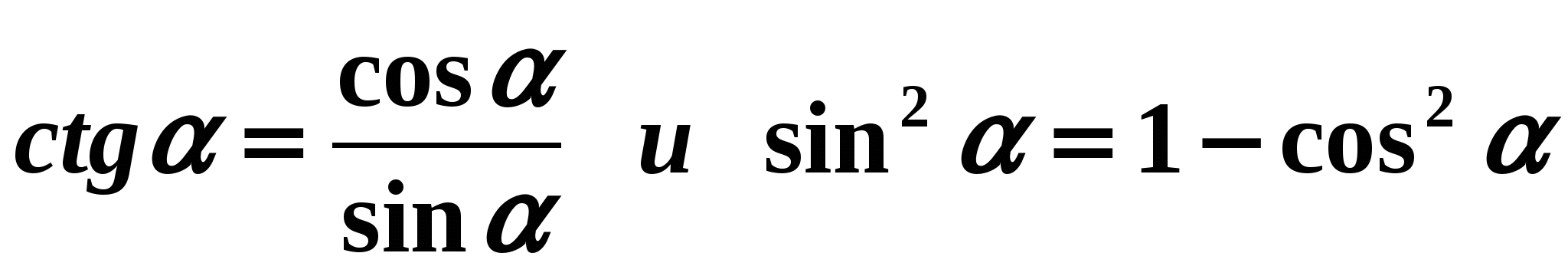 
. Mēs iegūstam: - Konsolidācija.
Un tagad uz ekrāna ir pašnovērtējuma rubrikas par šo tēmu. Atzīmējiet, kādu līmeni vēlaties sasniegt šodien.
Es sapratu tēmu un varu atrisināt piemērus pēc algoritma, skatoties burtnīcā, bet ar vadošo jautājumu palīdzību (kartīte - instrukcija).
Es saprotu tēmu un spēju atrisināt piemērus, izmantojot algoritmu, skatoties burtnīcā, izmantojot skolotāja norādījumus.
Es sapratu tēmu un varu atrisināt piemērus, izmantojot algoritmu, skatoties piezīmju grāmatiņā, bez vadošiem jautājumiem un norādījumiem.
Es sapratu tēmu un varu atrisināt piemērus, izmantojot algoritmu, neskatoties piezīmju grāmatiņā.
Neatkarīgi no tā, kuru līmeni izvēlaties, vispirms rūpīgi pārskatiet visus manis uzdotos uzdevumus un pēc tam izpildiet izvēlētajam līmenim atbilstošu uzdevumu (jūsu priekšā ir četru iespēju uzdevumi, opcijas numurs atbilst pašnodarbinātības līmeņiem novērtējums.)
1 variants
Instrukcija:
4 variants
Tagad, puiši, pārbaudīsim atbildes. Pareizās atbildes tiek parādītas ekrānā, un skolēni pārbauda savu darbu un ievieto punktus stundas kartītē Uzdevumi numur 4. Novērtējiet sevi stundu kartē. Aprēķiniet savus punktus un ievietojiet tos kartē.
- Mājasdarbs.
- Pierakstiet visas atvasinātās formulas atsauces grāmatā. Pēc mācību grāmatas Nr.459 (3, 5), Nr.460 (1)
Mēģināsim atrast sakarību starp viena un tā paša leņķa galvenajām trigonometriskajām funkcijām.
Attiecība starp viena un tā paša leņķa kosinusu un sinusu
Nākamajā attēlā ir parādīta Oxy koordinātu sistēma ar tajā attēlotu vienības pusloka ACB daļu, kas centrēta punktā O. Šī daļa ir vienības apļa loks. Vienības apli apraksta ar vienādojumu
- x2+y2=1.
Kā jau zināms, ordinātu y un abscisu x var attēlot kā leņķa sinusu un kosinusu, izmantojot šādas formulas:
- sin(a) = y,
- cos(a) = x.
Aizvietojot šīs vērtības vienības apļa vienādojumos, mēs iegūstam šādu vienādību
- (sin(a)) 2 + (cos(a)) 2 =1,
Šī vienādība attiecas uz visām leņķa a vērtībām. To sauc par pamata trigonometrisko identitāti.
No pamata trigonometriskās identitātes vienu funkciju var izteikt ar citu.
- sin(a) = ±√(1-(cos(a)) 2),
- cos(a) = ±√(1-(sin(a)) 2).
Šīs formulas labajā pusē esošo zīmi nosaka izteiksmes zīme šīs formulas kreisajā pusē.
Piemēram.
Aprēķiniet sin(a), ja cos(a)=-3/5 un pi Izmantosim iepriekš minēto formulu: Kopš pi Tagad mēģināsim atrast attiecības starp tangensu un kotangensiem. Pēc definīcijas tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a). Reizinot šīs vienādības, iegūstam tg(a)*ctg(a) =1. No šīs vienlīdzības vienu funkciju var izteikt ar citu. Mēs iegūstam: Jāsaprot, ka šīs vienādības ir spēkā tikai tad, ja pastāv tg un ctg, tas ir, jebkuram a, izņemot a = k * pi / 2, jebkuram veselam skaitlim k. Tagad mēģināsim izmantot pamata trigonometrisko identitāti, lai atrastu saistību starp tangensu un kosinusu. Sadaliet trigonometrisko pamatidentitāti ar (cos(a)) 2 . (cos(a) nav vienāds ar nulli, pretējā gadījumā tangensa nepastāvētu. Iegūstam šādu vienādību ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2 . Sadalot terminu ar terminu, mēs iegūstam: Kā minēts iepriekš, šī formula ir patiesa, ja cos(a) nav vienāds ar nulli, tas ir, visiem leņķiem a, izņemot a=pi/2 + pi*k, jebkuram veselam skaitlim k.Attiecība starp viena un tā paša leņķa tangensu un kotangensu