Vai tu tagad esi šeit? =) Nē, es necentos nevienu iebiedēt, vienkārši tēma par nepareizajiem integrāļiem ļoti labi parāda, cik svarīgi ir neskriet augstāko matemātiku u.c. eksaktās zinātnes. Lai apgūtu nodarbību vietnē, viss ir tur - detalizēti un pieejamu formu, būtu vēlme....
Tātad, sāksim. Tēlaini izsakoties, nepareizs integrālis ir “uzlabots” noteiktais integrālis, un patiesībā ar tiem nav tik daudz grūtību, turklāt nepareizajam integrālim ir ļoti laba ģeometriskā nozīme.
Ko nozīmē nepareiza integrāļa aprēķināšana?
Aprēķināt nepareizo integrāli - tas nozīmē atrast NUMURU(tieši tāds pats kā noteiktajam integrālim), vai pierādīt, ka tas atšķiras(tas ir, galu galā ar bezgalību skaitļa vietā).
Nepareizi integrāļi ir divu veidu.
Nepareizs integrālis ar bezgalīgu(-iem) integrācijas ierobežojumu(-iem).
Dažreiz tiek izsaukts šāds nepareizs integrālis nepareizs pirmā veida integrālis. IN vispārējs skats Nepareizs integrālis ar bezgalīgu ierobežojumu visbiežāk izskatās šādi: . Kā tas atšķiras no noteikta integrāļa? Augšējā robežā. Tas ir bezgalīgs:
Retāk sastopami integrāļi ar bezgalīgu apakšējo robežu vai ar divām bezgalīgām robežām: , un mēs tos apsvērsim vēlāk - kad jūs nobaudīsit :)
Nu, tagad analizēsim populārāko gadījumu. Lielākajā daļā piemēru integrand funkcija nepārtraukts pa vidu un šo svarīgs fakts, kas vispirms jāpārbauda! Jo, ja ir nepilnības, tad ir papildu nianses. Noteiktības labad mēs pieņemam, ka arī tad tipisks izliekta trapece izskatīsies šādi:
Ņemiet vērā, ka tas ir bezgalīgs (labajā pusē nav ierobežots) un nepareizs integrālis skaitliski vienāds ar tā laukumu. Šajā gadījumā ir iespējamas šādas iespējas:
1) Pirmā doma, kas nāk prātā, ir: “tā kā figūra ir bezgalīga, tad 
”, citiem vārdiem sakot, apgabals ir arī bezgalīgs. Tātad tā var būt.Šajā gadījumā mēs sakām, ka nepareizs integrālis atšķiras.
2) Bet. Lai cik paradoksāli tas neizklausītos, bezgalīgas figūras laukums var būt vienāds ar ... ierobežotu skaitli! Piemēram: . Tas varētu būt? Viegli. Otrajā gadījumā nepareizais integrālis saplūst.
3) Par trešo variantu nedaudz vēlāk.
Kad nepareizs integrālis atšķiras un kad tas saplūst? Tas ir atkarīgs no integrandas un konkrēti piemēri mēs ļoti drīz pārskatīsim.
Bet kas notiek, ja bezgalīga izliekta trapece atrodas zem ass? Šajā gadījumā nepareizs integrālis 
(atšķiras) vai vienāds ar finālu negatīvs skaitlis.
Tādējādi nepareizs integrālis var būt negatīvs.
Svarīgs! Ja jums tiek piedāvāts atrisināt JEBKURU nepareizu integrāli, tad, vispārīgi runājot, ne par kādu laukumu nav runas un nav jābūvē zīmējums. Es pastāstīju nepareizā integrāļa ģeometrisko nozīmi tikai tāpēc, lai būtu vieglāk saprast materiālu.
Tā kā nepareizais integrālis ir ļoti līdzīgs noteiktajam integrālim, mēs atceramies Ņūtona-Leibnica formulu: 
. Faktiski formula ir piemērojama arī nepareiziem integrāļiem, tikai tā ir nedaudz jāmaina. Kāda ir atšķirība? Integrācijas bezgalīgajā augšējā robežā: . Iespējams, daudzi ir uzminējuši, ka tas jau smaržo pēc robežu teorijas pielietošanas, un formula tiks uzrakstīta šādi: 
.
Kā tas atšķiras no noteikta integrāļa? Jā, nekas īpašs! Tāpat kā noteiktā integrālī, jums ir jāspēj atrast antiatvasināto funkciju (nenoteiktu integrāli), jāspēj pielietot Ņūtona-Leibnica formulu. Vienīgais, kas ir pievienots, ir limita aprēķins. Kuram ar viņiem slikti, pamācieties Funkciju ierobežojumi. Risinājumu piemēri jo labāk vēlāk nekā armijā.
Apsveriet divus klasiskus piemērus:
1. piemērs
Skaidrības labad es izveidošu zīmējumu, lai gan, vēlreiz uzsveru, uz praksi šajā uzdevumā nav nepieciešams veidot rasējumus.
Integrands ir nepārtraukts pusintervālā, kas nozīmē, ka viss ir kārtībā un nepareizo integrāli var aprēķināt, izmantojot “parasto” metodi.
Mūsu formulas pielietojums 
un risinājums izskatās šādi:
Tas ir, nepareizais integrālis atšķiras, un iekrāsotās līknes trapeces laukums ir vienāds ar bezgalību.
Aplūkotajā piemērā mums ir visvienkāršākais tabulu integrālis un tas pats paņēmiens Ņūtona-Leibnica formulas pielietošanai kā noteiktajam integrālim. Bet šī formula tiek piemērota zem ierobežojuma zīmes. Parastā "dinamiskā" mainīgā burta vietā parādās burts "be". Tam nevajadzētu mulsināt vai sajaukt, jo jebkurš burts nav sliktāks par standarta "X".
Ja jūs nesaprotat, kāpēc pie , tad tas ir ļoti slikti, vai nu jūs nesaprotat vienkāršākos ierobežojumus (un vispār nesaprotat, kas ir ierobežojums), vai arī jūs nezināt, kā izskatās grafiks logaritmiskā funkcija. Otrajā gadījumā apmeklējiet nodarbību Elementāro funkciju grafiki un īpašības.
Risinot nepareizos integrāļus, ir ļoti svarīgi zināt, kā izskatās galveno elementārfunkciju grafiki!
Tīram darba dizainam vajadzētu izskatīties apmēram šādi:
“
! Veidojot piemēru, mēs vienmēr pārtraucam risinājumu un norādām, kas notiek ar integrandu – vai tas ir nepārtraukts integrācijas intervālā vai nē. Ar to mēs identificējam nepareizā integrāļa veidu un pamatojam turpmākās darbības.
2. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Izveidosim zīmējumu: 
Pirmkārt, mēs novērojam sekojošo: integrands ir nepārtraukts pusintervālā . Labi. Risināšana ar formulu 
:
(1) Mēs ņemam vienkāršāko integrāli no jaudas funkcija(šis konkrētais gadījums ir atrodams daudzās tabulās). Mīnusu labāk uzreiz izņemt no robežzīmes, lai turpmākajos aprēķinos nepaliktu zem kājām.
(2) Mēs aizvietojam augšējo un apakšējo robežu saskaņā ar Ņūtona-Leibnica formulu.
(3) Mēs norādām, ka kad (Kungi, tas jau sen ir saprotams) un vienkāršojam atbildi.
Šeit bezgalīgas līknes trapeces laukums ir vienāds ar ierobežotu skaitli! Neticami, bet patiesi.
Piemēra tīrajam dizainam vajadzētu izskatīties apmēram šādi:
“
Integrands ir nepārtraukti ieslēgts
“
Ko darīt, ja sastopaties ar neatņemamu līdzīgu - ar Lūzuma punkts par integrācijas intervālu? Tas nozīmē, ka piemērā ir drukas kļūda (Visticamāk) vai paaugstināts izglītības līmenis. Pēdējā gadījumā sakarā ar aditivitātes īpašības, jāņem vērā divi nepareizi integrāļi intervālos un pēc tam jāapstrādā summa.
Dažreiz drukas kļūdas vai nepareiza integrāļa nolūka dēļ tas var notikt nemaz neeksistē, tātad, piemēram, ja ievietosim iepriekš minētā integrāļa saucēju Kvadrātsakne no "x", tad daļa no integrācijas intervāla vispār neiekļūs integranda definīcijas domēnā.
Turklāt nepareiza integrāļa var nebūt pat ar visu "šķietamo labklājību". Klasisks piemērs: . Neskatoties uz kosinusa noteiktību un nepārtrauktību, šāds nepareizs integrālis neeksistē! Kāpēc? Tas ir ļoti vienkārši, jo:
- neeksistē atbilstošā robeža.
Un šādi piemēri, lai arī reti, praksē ir sastopami! Tādējādi papildus konverģencei un diverģencei ir arī trešais risinājuma iznākums ar pilnu atbildi: "nav nepareiza integrāļa".
Jāņem vērā arī tas, ka nepareizā integrāļa stingra definīcija ir dota tieši caur robežu, un tie, kas vēlas, var ar to iepazīties mācību literatūrā. Nu, mēs turpinām praktiskā nodarbība un pārejiet pie jēgpilnākiem uzdevumiem:
3. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Vispirms mēģināsim atrast antiatvasināto funkciju (nenoteiktu integrāli). Ja mēs to neizdarīsim, tad, protams, mēs neatrisināsim arī nepareizo integrāli.
Kuram no tabulas integrāļiem izskatās integrands? Tas man atgādina loka tangensu: 
. No šiem apsvērumiem doma liek domāt, ka būtu jauki iegūt kvadrātu saucējā. Tas tiek darīts ar aizstāšanu.
Aizstāsim:
Nenoteiktais integrālis ir atrasts, pievienot konstanti šajā gadījumā nav jēgas.
Uzmetumā vienmēr ir lietderīgi veikt pārbaudi, tas ir, lai atšķirtu rezultātu:
Tika iegūts sākotnējais integrālists, kas nozīmē, ka nenoteiktais integrālis tika atrasts pareizi.
Tagad mēs atrodam nepareizo integrāli:
(1) Mēs rakstām risinājumu saskaņā ar formulu 
. Labāk ir nekavējoties pārvietot konstanti ārpus robežzīmes, lai tā netraucētu turpmākajiem aprēķiniem.
(2) Mēs aizstājam augšējo un apakšējo robežu saskaņā ar Ņūtona-Leibnica formulu. Kāpēc 
pie ? Skatiet loka tangentes grafiku jau vairākkārt ieteiktajā rakstā.
(3) Mēs saņemam galīgo atbildi. Tas, ka ir noderīgi zināt no galvas.
Padziļināti studenti var atsevišķi neatrast nenoteikto integrāli un neizmantot aizstāšanas metodi, bet izmantot funkciju summēšanas metodi zem diferenciālzīmes un nepareizo integrāli atrisināt "nekavējoties". Šajā gadījumā risinājumam vajadzētu izskatīties apmēram šādi:
“
Integrands ir nepārtraukts . 
“
4. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
! Šis ir tipisks piemērs, un līdzīgi integrāļi ir ļoti izplatīti. Izstrādājiet to labi! antiderivatīvā funkcijašeit ir atlases metode pilns kvadrāts, sīkāku informāciju par metodi var atrast nodarbībā Dažu frakciju integrācija.
5. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Šo integrāli var atrisināt detalizēti, tas ir, vispirms atrast nenoteikto integrāli, mainot mainīgo. Un jūs to varat atrisināt "tūlīt" - summējot funkciju zem diferenciāļa zīmes. Kam ir kaut kāda matemātiskā izglītība.
Pilnīgi risinājumi un atbildes nodarbības beigās.
Nepareizu integrāļu ar bezgalīgu apakšējo integrācijas robežu risinājumu piemērus var atrast lapā Efektīvas metodes nepareizu integrāļu risināšanai. Tur ir aplūkots arī gadījums, kad abas integrācijas robežas ir bezgalīgas.
Nepareizi neierobežotu funkciju integrāļi
Or nepareizi otrā veida integrāļi. Otrā veida nepareizie integrāļi tiek viltīgi "šifrēti" zem parastā noteiktā integrāļa un izskatās tieši tādi paši: Bet atšķirībā no noteiktā integrāļa integrands cieš no bezgalīgas pārtraukuma (nepastāv): 1) punktā, 2) vai punktā, 3) vai abos punktos uzreiz, 4) vai pat integrācijas intervālā. Mēs izskatīsim pirmos divus gadījumus, 3-4 gadījumiem raksta beigās ir saite uz papildu nodarbību.
Tikai piemērs, lai būtu skaidrs:. Šķiet, ka tas ir noteikts integrālis. Bet patiesībā tas ir nepareizs otrā veida integrālis, ja integrandā aizstājam apakšējās robežas vērtību, tad saucējs pazūd, tas ir, integrands šajā brīdī vienkārši nepastāv!
Kopumā, analizējot nepareizo integrāli vienmēr ir nepieciešams aizvietot abus integrācijas ierobežojumus integrandā. Šajā sakarā mēs pārbaudām arī augšējo robežu: 
. Šeit viss ir labi.
Līklīnijas trapecveida nepareizā integrāļa izskatāmajai dažādībai būtībā izskatās šādi:
Šeit gandrīz viss ir tāds pats kā pirmā veida integrālī.
Mūsu integrālis ir skaitliski vienāds ar iekrāsotās līknes trapeces laukumu, kas nav ierobežots no augšas. Šajā gadījumā var būt divas iespējas *: nepareizais integrālis atšķiras (laukums ir bezgalīgs) vai nepareizais integrālis ir vienāds ar ierobežotu skaitli (tas ir, bezgalīgas figūras laukums ir ierobežots!).
* pēc noklusējuma mēs parasti pieņemam, ka nepareizais integrālis pastāv
Atliek tikai modificēt Ņūtona-Leibnica formulu. To arī modificē ar limita palīdzību, bet robeža vairs netiecas uz bezgalību, bet uz vērtību labajā pusē. Ir viegli sekot līdzi zīmējumam: gar asi mums ir jātuvojas lūzuma punktam bezgalīgi tuvu labajā pusē.
Apskatīsim, kā tas tiek īstenots praksē.
6. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Integrands kādā punktā cieš bezgalīgu pārtraukumu (neaizmirstiet mutiski vai uzmetumā pārbaudīt, vai ar augšējo robežu viss ir kārtībā!)
Pirmkārt, mēs aprēķinām nenoteikto integrāli: 
Aizstāšana: 
Tiem, kuriem ir grūtības ar nomaiņu, skatiet nodarbību Aizstāšanas metode nenoteiktā integrālā.
Mēs aprēķinām nepareizo integrāli:
(1) Kas jauns šeit? Tehnikas ziņā praktiski nekā. Vienīgais, kas ir mainījies, ir ieraksts zem ierobežojuma ikonas: . Papildinājums nozīmē, ka mēs mērķējam uz vērtību labajā pusē (kas ir loģiski - skatiet grafiku). Tādu robežu robežu teorijā sauc vienpusējs ierobežojums. Šajā gadījumā mums ir labās puses ierobežojums.
(2) Mēs aizvietojam augšējo un apakšējo robežu saskaņā ar Ņūtona-Leibnica formulu.
(3) Nodarbojas ar . Kā noteikt, kur atrodas izteiksme? Aptuveni runājot, jums vienkārši jāaizstāj vērtība, jāaizstāj trīs ceturtdaļas un jānorāda, ka . Atbildes ķemmēšana.
Šajā gadījumā nepareizais integrālis ir vienāds ar negatīvu skaitli. Šeit nav nozieguma, tikai atbilstošā izliekuma trapece atrodas zem ass.
Un tagad divi piemēri neatkarīgam risinājumam.
7. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
8. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Ja integrands punktā neeksistē
Bezgalīga izliekta trapecveida forma šādam nepareizam integrālam būtībā izskatās šādi.
Noteikts integrālis kā integrāļa summas robeža
var pastāvēt (t.i., tam ir noteikta galīgā vērtība) tikai tad, ja ir izpildīti nosacījumi
Ja tiek pārkāpts vismaz viens no šiem nosacījumiem, definīcija zaudē savu nozīmi. Patiešām, bezgalīga segmenta gadījumā, piemēram, [ a; ) to nevar sadalīt P ierobežota garuma daļas 
, kas turklāt, palielinoties segmentu skaitam, būtu tendence uz nulli. Neierobežotu gadījumā kādā brīdī Ar[a;
b] tiek pārkāpta punkta patvaļīgas izvēles prasība 
daļējos segmentos – nevar atlasīt 
=Ar, jo funkcijas vērtība šajā brīdī nav definēta. Tomēr noteikta integrāļa jēdzienu var vispārināt arī šiem gadījumiem, pievienojot robežai vēl vienu fragmentu. Tiek izsaukti integrāļi bezgalīgos intervālos un no pārtrauktām (neierobežotām) funkcijām nepiederošs.
Definīcija.
Ļaujiet funkcijai 
definēts intervālā [ a; ) un ir integrējams jebkurā ierobežotā intervālā [ a;
b], t.i. pastāv 
jebkuram b
> a. skata ierobežojums 
sauca nepareizs integrālis
pirmais veids
(vai ar nepareizu integrāli bezgalīgā intervālā) un apzīmē 
.
Tādējādi pēc definīcijas 
=
.
Ja labās puses robeža pastāv un ir ierobežota, tad nepareizais integrālis 
sauca saplūst
. Ja šī robeža ir bezgalīga vai vispār nepastāv, tad tiek uzskatīts, ka nepareizais integrālis ir atšķiras
.
Līdzīgi mēs varam ieviest nepareiza funkcijas integrāļa jēdzienu 
pēc intervāla (–; b]:
=
.
Un nepareizs funkcijas integrālis 
intervālā (–; +) ir definēts kā iepriekš ievadīto integrāļu summa:
=
+
,
Kur A ir patvaļīgs punkts. Šis integrālis saplūst, ja abi termini saplūst, un atšķiras, ja vismaz viens no terminiem atšķiras.
No ģeometriskā viedokļa integrālis 
,
, nosaka bezgalīgas līknes trapeces laukuma skaitlisko vērtību, kuru no augšas ierobežo funkcijas grafiks 
, pa kreisi - taisni 
, no apakšas - VĒRSIS ass. Integrāļa konverģence nozīmē šādas trapeces noteikta laukuma esamību un tā vienādību ar līknes trapeces laukuma robežu ar kustīgu labo sienu 
.
Integrāļa gadījumā ar bezgalīgu robežu var arī vispārināt Ņūtona-Leibnica formula:
=
=F( +
) – F( a),
kur F( +
)
=
. Ja šī robeža pastāv, tad integrālis saplūst, pretējā gadījumā tas atšķiras.
Mēs esam apsvēruši noteikta integrāļa jēdziena vispārinājumu bezgalīga intervāla gadījumā.
Tagad apskatīsim vispārinājumu neierobežotas funkcijas gadījumam.
Definīcija
Ļaujiet funkcijai 
definēts intervālā [ a;
b), ir neierobežots kādā punkta apkārtnē b, un ir nepārtraukts jebkurā segmentā 
, kur>0 (un līdz ar to ir integrējams šajā segmentā, t.i. 
pastāv). skata ierobežojums 
sauca nepareizs otrā veida integrālis
(vai ar neierobežotas funkcijas nepareizu integrāli) un tiek apzīmēts 
.
Tādējādi nepareizais neierobežotais integrālis punktā b funkcijas ir pēc definīcijas
=
.
Ja labās puses robeža pastāv un ir ierobežota, tad tiek izsaukts integrālis saplūst. Ja nav galīgas robežas, tad tiek izsaukts nepareizais integrālis atšķiras.
Līdzīgi var definēt nepareizu funkcijas integrāli 
ar bezgalīgu pārtraukumu punktā A:
=
.
Ja funkcija 
iekšējā punktā ir bezgalīgs pārtraukums Ar
, tad nepareizais integrālis tiek definēts šādi
=
+
=
+
.
Šis integrālis saplūst, ja abi termini saplūst, un atšķiras, ja atšķiras vismaz viens termins.
No ģeometriskā viedokļa nepareizs neierobežotas funkcijas integrālis raksturo arī neierobežotas līknes trapeces laukumu:
Tā kā nepareizais integrālis tiek iegūts, pārejot uz robežu no noteiktā integrāļa, tad visas noteiktā integrāļa īpašības var pārnest (ar atbilstošiem precizējumiem) uz pirmā un otrā veida nepareizajiem integrāļiem.
Daudzās problēmās, kas noved pie nepareiziem integrāļiem, nav jāzina, ar ko šis integrālis ir vienāds, pietiek tikai pārliecināties, vai tas saplūst vai atšķiras. Šim lietojumam konverģences pazīmes. Nepareizu integrāļu konverģences pazīmes:
1) Salīdzinājuma zīme.
Ļaujiet visiem X
. Tad ja 
saplūst, tad saplūst un 
, un 
. Ja 
atšķiras, tad atšķiras un 
.
2) Ja saplūst 
, tad saplūst un 
(šajā gadījumā tiek saukts pēdējais integrālis absolūti konverģents).
Neierobežotu funkciju nepareizo integrāļu konverģences un diverģences kritēriji ir līdzīgi iepriekš formulētajiem.
Problēmu risināšanas piemēri.
1. piemērs
A) 
; b) 
; V) 
G) 
; e) 
.
Risinājums.
a) Pēc definīcijas mums ir:
.
b) Līdzīgi
Tāpēc šis integrālis saplūst un ir vienāds ar 
.
c) Pēc definīcijas 
=
+
, Turklāt, A ir patvaļīgs skaitlis. Ieliksim savā lietā 
, tad mēs iegūstam:
Šis integrālis saplūst.
Tātad šis integrālis atšķiras.
e) Apsveriet 
. Lai atrastu integranda antiatvasinājumu, ir jāpiemēro integrācijas pa daļām metode. Tad mēs iegūstam:
Tā kā ne viens, ne otrs 
, ne 
neeksistē, tad neeksistē un
Tāpēc šis integrālis atšķiras.
2. piemērs
Pētīt integrāļa konverģenci 
atkarībā no P.
Risinājums.
Plkst 
mums ir:
Ja 
, Tas 
Un. Tāpēc integrālis atšķiras.
Ja 
, Tas 
, A 
, Tad
=,
Tāpēc integrālis saplūst.
Ja 
, Tas
tāpēc integrālis atšķiras.
Tādējādi 
3. piemērs
Aprēķiniet nepareizo integrāli vai iestatiet tā novirzi:
A) 
; b) 
; V) 
.
Risinājums.
a) Integrāls 
ir nepareizs otrā veida integrālis, jo integrands 
nav ierobežots vienā punktā 
. Tad pēc definīcijas
.
Integrālis saplūst un ir vienāds ar 
.
b) Apsveriet 
. Arī šeit integrands nav ierobežots punktā 
. Tāpēc šis integrālis ir nepareizs otrā veida un pēc definīcijas
Tāpēc integrālis atšķiras.
c) Apsveriet 
. Integrand 
cieš bezgalīgs pārtraukums divos punktos: 
Un 
, no kuriem pirmais pieder integrācijas intervālam 
. Tāpēc šis integrālis ir nepareizs no otrā veida. Tad pēc definīcijas
=
=
.
Tāpēc integrālis saplūst un ir vienāds ar 
.
Noteikts integrālis
\[ I=\int_a^bf(x)dx \]
tika konstruēts, pieņemot, ka skaitļi $a,\,b$ ir galīgi un $f(x)$ ir nepārtraukta funkcija. Ja kāds no šiem pieņēmumiem tiek pārkāpts, tiek runāts par nepareiziem integrāļiem.
10.1. Nepareizi 1. veida integrāļi
Nepareizs pirmā veida integrālis rodas, ja vismaz viens no skaitļiem $a,\,b$ ir bezgalīgs.
10.1.1. Definīcija un pamatīpašības
Vispirms apskatīsim situāciju, kad integrācijas apakšējā robeža ir ierobežota un augšējā robeža ir vienāda ar $+\infty$; citas iespējas tiks apspriestas vēlāk. Ja $f(x)$ ir nepārtraukts visiem $x$, kas mūs interesē, apsveriet integrāli
\begin(vienādojums) I=\int _a^(+\infty)f(x)dx. \quad(19) \label(inf1) \end(vienādojums)
Pirmkārt, ir jānosaka šī izteiciena nozīme. Lai to izdarītu, mēs ieviešam funkciju
\[ I(N)=\int _a^(N)f(x)dx \]
un uzskata to par $N\rightarrow +\infty$.
Definīcija. Lai ir robeža
\[ A=\lim_(N \rightarrow +\infty)I(N)=\lim_(N \rightarrow +\infty)\int _a^(N)f(x)dx. \]
Tad tiek teikts, ka 1. veida nepareizais integrālis (19) saplūst un tam tiek piešķirta vērtība $A$, pati funkcija tiek saukta par integrējamu intervālā $\left[ a, \, +\infty \right)$ . Ja norādītā robeža nepastāv vai tā ir vienāda ar $\pm \infty$, tad tiek uzskatīts, ka integrālis (19) atšķiras.
Apsveriet integrāli
\[ I=\int _0^(+\infty) \frac(dx)(1+x^2). \]
\[ I(N)=\int _0^(N) \frac(dx)(1+x^2). \]
Šajā gadījumā ir zināms integrandas antiatvasinājums, tāpēc
\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)=arctgx|_0^(N)=arctgN. \]
Ir zināms, ka $arctg N \rightarrow \pi /2 $ for $N \rightarrow +\infty$. Tādējādi $I(N)$ ir ierobežots ierobežojums, mūsu nepareizais integrālis saplūst un ir vienāds ar $\pi /2$.
Saplūstošiem 1. veida nepareizajiem integrāļiem ir visas parasto noteikto integrāļu standarta īpašības.
1. Ja $f(x)$, $g(x)$ ir integrējami intervālā $\left[ a, \, +\infty \right)$, tad to summa $f(x)+g(x) $ is ir arī integrējams šajā intervālā, un \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx. \] 2. Ja $f(x)$ ir integrējams intervālā $\left[ a, \, +\infty \right)$, tad jebkurai konstantei $C$ funkcija $C\cdot f(x)$ ir arī integrējams šajā intervālā, un \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx. \] 3. Ja $f(x)$ ir integrējams intervālā $\left[ a, \, +\infty \right)$ un $f(x)>0$ šajā intervālā, tad \[ \int _a ^ (+\infty) f(x)dx\,>\,0. \] 4. Ja $f(x)$ ir integrējams intervālā $\left[ a, \, +\infty \right)$, tad jebkuram $b>a$ integrālis \[ \int _b^(+ \infty) f(x)dx \] saplūst, un \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty ) f(x)dx \] (integrāļa saskaitāmība pa intervālu).
Der arī formulas mainīgā lieluma maiņai, integrācijai pa daļām utt. (ar dabas rezervātiem).
Apsveriet integrāli
\begin(vienādojums) I=\int _1^(+\infty)\frac(1)(x^k)\,dx. \quad (20) \label(mod) \end(vienādojums)
Mēs iepazīstinām ar funkciju
\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx. \]
Šajā gadījumā antiderivatīvs ir zināms, tā ka
\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k)|_1^N = \frac(N^(1-k))(1-k)-\frac(1)(1-k) \]
par $k \neq 1$,
\[ I(N)=\int _1^(N)\frac(1)(x)\,dx\,=lnx|_1^N= lnN \]
par $k = 1$. Ņemot vērā $N \rightarrow +\infty$ uzvedību, mēs nonākam pie secinājuma, ka integrālis (20) saplūst $k>1$ un atšķiras $k \leq 1$.
Tagad apskatīsim iespēju, kad integrācijas apakšējā robeža ir vienāda ar $-\infty$, bet augšējā ir ierobežota, t.i. ņemiet vērā integrāļus
\[ I=\int _(-\infty)^af(x)dx. \]
Taču šo variantu var reducēt uz iepriekšējo, ja veicam mainīgo $x=-s$ maiņu un pēc tam samainām integrācijas robežas, lai
\[ I=\int _(-a)^(+\infty)g(s)ds, \]
$g(s)=f(-s)$. Tagad aplūkosim gadījumu, kad ir divas bezgalīgas robežas, t.i. neatņemama
\begin(vienādojums) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(vienādojums)
kur $f(x)$ ir nepārtraukts visiem $x \in \mathbb(R)$. Sadalīsim intervālu divās daļās: ņemsim $c \in \mathbb(R)$ un apsveriet divus integrāļus,
\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx. \]
Definīcija. Ja abi integrāļi $I_1$, $I_2$ saplūst, tad integrāli (21) sauc par konverģentu, tam tiek piešķirta vērtība $I=I_1+I_2$ (atbilstoši intervāla aditivitātei). Ja vismaz viens no integrāļiem $I_1$, $I_2$ atšķiras, integrālis (21) tiek uzskatīts par diverģentu.
Var pierādīt, ka integrāļa (21) konverģence nav atkarīga no punkta $c$ izvēles.
Nepareiziem 1. veida integrāļiem ar integrācijas intervāliem $\left(-\infty, \, c \right]$ vai $(-\infty, \, +\infty)$ ir arī visas noteikto integrāļu standarta īpašības (ar atbilstošā pārformulācija, kurā ņemts vērā izvēles integrācijas intervāls).
10.1.2. Pirmā veida nepareizo integrāļu konverģences kritēriji
Teorēma (pirmā salīdzinājuma zīme). Ļaujiet $f(x)$, $g(x)$ būt nepārtrauktiem $x>a$ un $0 a$. Tad
1. Ja integrālis \[ \int _a^(+\infty)g(x)dx \] saplūst, tad arī integrālis \[ \int _a^(+\infty)f(x)dx saplūst. \] 2. Ja integrālis \[ \int _a^(+\infty)f(x)dx \] atšķiras, tad arī integrālis \[ \int _a^(+\infty)g(x)dx atšķiras. \]
Teorēma (otrā salīdzinājuma zīme). Lai $f(x)$, $g(x)$ ir nepārtraukti un pozitīvi attiecībā uz $x>a$, un lai ir ierobežots ierobežojums
\[ \theta = \lim_(x \rightarrow +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]
Tad integrāļi
\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]
vienā un tajā pašā laikā saplūst vai atšķiras.
Apsveriet integrāli
\[ I=\int _1^(+\infty)\frac(1)(x+\sin x)\,dx. \]
Integrands ir pozitīva funkcija integrācijas intervālā. Turklāt par $x \rightarrow +\infty$ mums ir:
$\sin x$ ir "neliels" saucēja labojums. Precīzāk, ja ņemam $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, tad
\[ \lim _(x \rightarrow +\infty)\frac(f(x))(g(x))=\lim _(x \rightarrow +\infty)\frac(x)(x+\sin x) =1. \]
Piemērojot otro salīdzināšanas kritēriju, mēs nonākam pie secinājuma, ka mūsu integrālis konverģē vai diverģē vienlaikus ar integrāli
\[ \int _1^(+\infty)\frac(1)(x)\,dx . \]
Kā parādīts iepriekšējā piemērā, šis integrālis atšķiras ($k=1$). Tāpēc sākotnējais integrālis atšķiras.
Aprēķiniet nepareizo integrāli vai nosakiet tā konverģenci (diverģenci).
1. \[ \int _(0)^(+\infty)e^(-ax)\,dx. \] 2. \[ \int _(0)^(+\infty)xe^(-x^2)\,dx. \] 3. \[ \int _(-\infty)^(+\infty)\frac(2xdx)(x^2+1). \] 4. \[ \int _(0)^(+\infty)\frac(xdx)((x+2)^3). \] 5. \[ \int _(-\infty)^(+\infty)\frac(dx)(x^2+2x+2). \] 6. \[ \int _(1)^(+\infty)\frac(lnx)(x^2)\,dx. \] 7. \[ \int _(1)^(+\infty)\frac(dx)((1+x)\sqrt(x)). \] 8. \[ \int _(0)^(+\infty)e^(-\sqrt(x))\,dx. \] 9. \[ \int _(0)^(+\infty)e^(-ax)\cos x\,dx. \] 10. \[ \int _(0)^(+\infty)\frac(xdx)(x^3+1). \]
Nepareizs integrālis ar bezgalīgu integrācijas ierobežojumu
Dažreiz šādu nepareizu integrāli sauc arī par nepareizu pirmā veida integrāli..gif" width="49" height="19 src=">.
Retāk sastopami integrāļi ar bezgalīgu apakšējo robežu vai ar divām bezgalīgām robežām: .
Mēs apsvērsim populārāko gadījumu https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Nē ne vienmēr. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">
Attēlosim integranda grafiku zīmējumā. Tipisks grafiks un līknes trapecveida forma šim gadījumam izskatās šādi:
Nepareizs integrālishttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", citiem vārdiem sakot, apgabals ir arī bezgalīgs. Tātad tā var būt.Šajā gadījumā mēs sakām, ka nepareizs integrālis atšķiras.
2) Bet. Lai cik paradoksāli tas neizklausītos, bezgalīgas figūras laukums var būt vienāds ar ... ierobežotu skaitli! Piemēram: .. Otrajā gadījumā nepareizais integrālis saplūst.
Un kas notiek, ja bezgalīga izliekta trapecveida forma atrodas zem ass?.gif" width="217" height="51 src=">.
: 
.
1. piemērs
Integrāde https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, kas nozīmē, ka viss ir kārtībā un nepareizo integrāli var aprēķināt, izmantojot " parastā metode.
Mūsu formulas pielietošana https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">
Tas ir, nepareizais integrālis atšķiras, un iekrāsotās līknes trapeces laukums ir vienāds ar bezgalību.
Risinot nepareizos integrāļus, ir ļoti svarīgi zināt, kā izskatās galveno elementārfunkciju grafiki!
2. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Izveidosim zīmējumu: 
Pirmkārt, mēs novērojam sekojošo: integrands ir nepārtraukts pusintervālā . Labi..gif" width="327" height="53">
(1) Mēs ņemam vienkāršāko jaudas funkcijas integrāli (šis īpašais gadījums ir daudzās tabulās). Mīnusu labāk uzreiz izņemt no robežzīmes, lai turpmākajos aprēķinos nepaliktu zem kājām.
(2) Mēs aizvietojam augšējo un apakšējo robežu saskaņā ar Ņūtona-Leibnica formulu.
(3) Mēs norādām, ka https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (kungi, tas jau sen ir saprotams) un vienkāršojam atbildi.
Šeit bezgalīgas līknes trapeces laukums ir vienāds ar ierobežotu skaitli! Neticami, bet patiesi.
3. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Integrands ir nepārtraukts .
Vispirms mēģināsim atrast antiatvasināto funkciju (nenoteiktu integrāli).
Kuram no tabulas integrāļiem izskatās integrands? Tas man atgādina loka tangensu: 
. No šiem apsvērumiem doma liek domāt, ka būtu jauki iegūt kvadrātu saucējā. Tas tiek darīts ar aizstāšanu.
Aizstāsim:
Vienmēr ir lietderīgi veikt pārbaudi, tas ir, lai diferencētu iegūto rezultātu:
Tagad mēs atrodam nepareizo integrāli:
(1) Mēs rakstām risinājumu saskaņā ar formulu 
. Labāk ir nekavējoties pārvietot konstanti ārpus robežzīmes, lai tā netraucētu turpmākajiem aprēķiniem.
(2) Mēs aizstājam augšējo un apakšējo robežu saskaņā ar Ņūtona-Leibnica formulu..gif" width="56" height="19 src=">?
(3) Mēs saņemam galīgo atbildi. Tas, ka ir noderīgi zināt no galvas.
Padziļināti studenti var atsevišķi neatrast nenoteikto integrāli un neizmantot aizstāšanas metodi, bet izmantot funkciju summēšanas metodi zem diferenciālzīmes un nepareizo integrāli atrisināt "nekavējoties". Šajā gadījumā risinājumam vajadzētu izskatīties apmēram šādi:
“
Integrāde ir nepārtraukta vietnē https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“
4. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
! Šis ir tipisks piemērs, un līdzīgi integrāļi ir ļoti izplatīti. Izstrādājiet to labi! Antiderivatīvā funkcija šeit atrodama ar pilna kvadrāta atlases metodi.
5. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Šo integrāli var atrisināt detalizēti, tas ir, vispirms atrast nenoteikto integrāli, mainot mainīgo. Un jūs to varat atrisināt "nekavējoties" - summējot funkciju zem diferenciāļa zīmes ..
Nepareizi neierobežotu funkciju integrāļi
Dažreiz šādus nepareizos integrāļus sauc par otrā veida nepareizajiem integrāļiem. Nepareizi otrā veida integrāļi tiek viltīgi "šifrēti" zem parastā noteiktā integrāļa un izskatās tieši tāpat: ..gif" width="39" height="15 src=">, 2) vai punktā , 3) vai abos punktos uzreiz, 4) vai pat integrācijas intervālā. Mēs izskatīsim pirmos divus gadījumus, 3.-4. gadījumam raksta beigās ir saite uz papildu nodarbību.
Tikai piemērs, lai būtu skaidrs: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, tad mūsu saucējs kļūst par nulli, tas ir, integrands šajā brīdī vienkārši nepastāv!
Kopumā, analizējot nepareizo integrāli vienmēr ir nepieciešams aizvietot abus integrācijas ierobežojumus integrandā..jpg" alt="Nepareizs integrālis, pārtraukuma punkts integrācijas apakšējā robežā" width="323" height="380">!}
Šeit gandrīz viss ir tāds pats kā pirmā veida integrālī.
Mūsu integrālis ir skaitliski vienāds ar iekrāsotās līknes trapeces laukumu, kas nav ierobežots no augšas. Šajā gadījumā var būt divas iespējas: nepareizais integrālis atšķiras (laukums ir bezgalīgs) vai nepareizais integrālis ir vienāds ar ierobežotu skaitli (tas ir, bezgalīgas figūras laukums ir ierobežots!).
Atliek tikai modificēt Ņūtona-Leibnica formulu. To arī modificē ar limita palīdzību, bet robeža vairs netiecas uz bezgalību, bet novērtēthttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> labajā pusē.
6. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Integrands kādā punktā cieš bezgalīgu pārtraukumu (neaizmirstiet mutiski vai uzmetumā pārbaudīt, vai ar augšējo robežu viss ir kārtībā!)
Pirmkārt, mēs aprēķinām nenoteikto integrāli: 
Aizstāšana: 
Mēs aprēķinām nepareizo integrāli:
(1) Kas jauns šeit? Tehnikas ziņā praktiski nekā. Vienīgais, kas ir mainījies, ir ieraksts zem ierobežojuma ikonas: . Papildinājums nozīmē, ka mēs mērķējam uz vērtību labajā pusē (kas ir loģiski - skatiet grafiku). Šādu robežu robežu teorijā sauc par vienpusēju robežu. Šajā gadījumā mums ir labās puses ierobežojums.
(2) Mēs aizvietojam augšējo un apakšējo robežu saskaņā ar Ņūtona-Leibnica formulu.
(3) Izpratne par https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Kā noteikt, kur šī izteiksme jānovirza? Aptuveni runājot, jums vienkārši jāaizstāj ar to vērtību, jāaizstāj trīs ceturtdaļas un jānorāda, ka... Mēs ķemmējam atbildi.
Šajā gadījumā nepareizais integrālis ir vienāds ar negatīvu skaitli.
7. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
8. piemērs
Aprēķiniet nepareizo integrāli vai nosakiet tā novirzi.
Ja integrands punktā neeksistē
Bezgalīga izliekta trapece šādam nepareizam integrālam būtībā izskatās šādi:
Šeit viss ir tieši tāpat, izņemot to, ka robeža mēdz novērtēthttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> mums ir jānokļūst bezgalīgi tuvu lūzuma punktam pa kreisi.
Nepareizi pirmā veida integrāļi: koncepcijas izplatīšana noteikts integrālis integrāļu gadījumiem ar bezgalīgām integrācijas augšējām vai apakšējām robežām, vai arī abas integrācijas robežas ir bezgalīgas.
Nepareizi otrā veida integrāļi: noteikta integrāļa jēdziena paplašināšana uz neierobežotu funkciju integrāļu gadījumiem, integrands neeksistē galīgā integrācijas intervāla punktu skaitā, pagriežoties uz bezgalību.
Salīdzinājumam. Ieviešot noteikta integrāļa jēdzienu, tika pieņemts, ka funkcija f(x) ir nepārtraukts segmentā [ a, b], un integrācijas intervāls ir ierobežots, tas ir, to ierobežo skaitļi, nevis bezgalība. Daži uzdevumi rada nepieciešamību atteikties no šiem ierobežojumiem. Šādi parādās nepareizi integrāļi.
Nepareizā integrāļa ģeometriskā nozīme izrādās pavisam vienkārši. Kad funkcijas grafiks y = f(x) atrodas virs ass Vērsis, noteiktais integrālis izsaka līknes trapeces laukumu, ko ierobežo līkne y = f(x) , abscisa un ordinātas x = a , x = b. Savukārt nepareizais integrālis izsaka starp līnijām norobežotas (bezgalīgas) līklīnijas trapeces laukumu y = f(x) (attēlā zemāk sarkanā krāsā) x = a un abscisu ass.
Nepareizi integrāļi tiek definēti līdzīgi citiem bezgalīgiem intervāliem:
Bezgalīgas līknes trapeces laukums var būt ierobežots skaitlis, un šajā gadījumā nepareizo integrāli sauc par konverģentu. Laukums var būt arī bezgalība, un tādā gadījumā nepareizo integrāli sauc par diverģentu.
Integrāļa robežas izmantošana paša nepareizā integrāļa vietā. Lai aprēķinātu nepareizo integrāli, ir jāizmanto noteiktā integrāļa robeža. Ja šī robeža pastāv un ir ierobežota (nav vienāda ar bezgalību), tad nepareizo integrāli sauc par konverģentu, pretējā gadījumā tas ir diverģents. Tas, uz ko mēdz būt mainīgais zem ierobežojuma zīmes, ir atkarīgs no tā, vai mums ir darīšana ar nepareizu pirmā vai otrā veida integrāli. Uzzināsim par to tagad.
Nepareizi pirmā veida integrāļi - ar bezgalīgiem ierobežojumiem un to konverģenci
Nepareizi integrāļi ar bezgalīgu augšējo robežu
Tātad nepareizā integrāļa ieraksts atšķiras no parastā noteiktā integrāļa ar to, ka integrācijas augšējā robeža ir bezgalīga.
Definīcija. Nepareizs integrālis ar bezgalīgu augšējo integrācijas robežu no nepārtraukta funkcija f(x) starp a pirms tam ∞ sauc par šīs funkcijas integrāļa robežu ar integrācijas augšējo robežu b un integrācijas apakšējā robeža a ar nosacījumu, ka integrācijas augšējā robeža pieaug uz nenoteiktu laiku, t.i.
.
Ja šī robeža pastāv un ir vienāda ar kādu skaitli, nevis ar bezgalību, tad nepareizo integrāli sauc par konverģentu, un par tā vērtību tiek ņemts skaitlis, kas vienāds ar ierobežojumu. Citādi nepareizo integrāli sauc par diverģentu un tam netiek piešķirta nekāda vērtība.
1. piemērs. Aprēķināt nepareizo integrāli(ja tas saplūst).
Risinājums. Pamatojoties uz nepareizā integrāļa definīciju, mēs atrodam
Tā kā robeža pastāv un ir vienāda ar 1, tad dotā nepareizs integrālis saplūst un ir vienāds ar 1.
Nākamajā piemērā integrands ir gandrīz tāds pats kā 1. piemērā, tikai x pakāpe nav divi, bet gan burts alfa, un uzdevums ir izpētīt konverģences nepareizo integrāli. Tas nozīmē, ka joprojām ir jāatbild uz jautājumu: pie kādām alfa vērtībām šis nepareizais integrālis saplūst un pie kādām vērtībām tas atšķiras?
2. piemērs. Izpētiet nepareiza integrāļa konverģenci(apakšējā integrācijas robeža ir lielāka par nulli).
Risinājums. Pieņemsim, ka vispirms, tad
Iegūtajā izteiksmē mēs pārejam uz robežu pie :
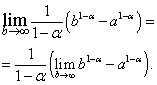
Ir viegli redzēt, ka labajā pusē pastāv ierobežojums un nulle, kad , tas ir , un neeksistē kad , tas ir .
Pirmajā gadījumā tas ir, kad . Ja tad 
un neeksistē.
Mūsu pētījuma secinājums ir šāds: nepareizs integrālis saplūst un atšķiras plkst.
Piemērojot pētītajam nepareizā integrāļa veidam Ņūtona-Leibnica formulu 
, mēs varam iegūt šādu ļoti līdzīgu formulu:
.
Šī ir vispārinātā Ņūtona-Leibnica formula.
3. piemērs. Aprēķiniet nepareizo integrāli(ja tas saplūst).
Šī integrāļa ierobežojums pastāv:
Otrais integrālis, kas ir summa, kas izsaka sākotnējo integrāli:
Pastāv arī šī integrāļa ierobežojums:
.
Mēs atrodam divu integrāļu summu, kas ir arī sākotnējā nepareizā integrāļa vērtība ar divām bezgalīgām robežām:
Nepareizi otrā veida integrāļi - no neierobežotām funkcijām un to konverģences
Ļaujiet funkcijai f(x) iestatīts uz segmentu no a pirms tam b un neierobežots. Pieņemsim, ka funkcija punktā iet līdz bezgalībai b , savukārt visos pārējos segmenta punktos tas ir nepārtraukts.
Definīcija. Nepareizs funkcijas integrālis f(x) segmentā no a pirms tam b sauc par šīs funkcijas integrāļa robežu ar integrācijas augšējo robežu c , ja cenšoties c Uz b funkcija palielinās bezgalīgi, un punktā x = b funkcija nav definēta, t.i.
.
Ja šī robeža pastāv, tad otrā veida nepareizo integrāli sauc par konverģentu, pretējā gadījumā par diverģentu.
Izmantojot Ņūtona-Leibnica formulu, mēs iegūstam.