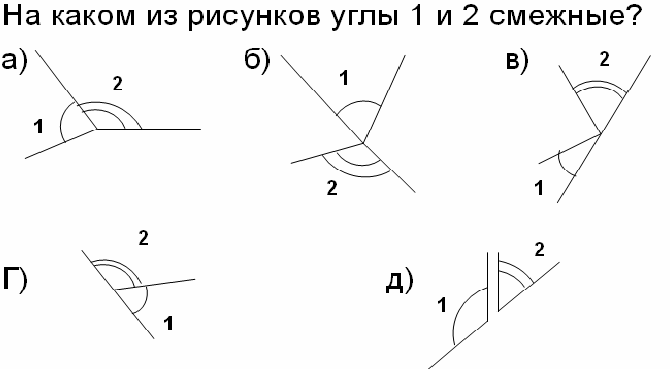
Dy kënde quhen ngjitur nëse kanë një anë të përbashkët, dhe anët e tjera të këtyre këndeve janë rreze plotësuese. Në figurën 20, këndet AOB dhe BOC janë ngjitur.
Shuma qoshet ngjitur e barabartë me 180°
Teorema 1. Shuma e këndeve ngjitur është 180°.
Dëshmi. Trau OB (shih Fig. 1) kalon midis anëve të këndit të shpalosur. Kjo është arsyeja pse ∠ AOB + ∠ BOS = 180°.
Nga teorema 1 rezulton se nëse dy kënde janë të barabartë, atëherë këndet e tyre ngjitur janë të barabartë.
Këndet vertikale janë të barabarta
Dy kënde quhen vertikale nëse brinjët e njërit kënd janë rreze plotësuese të brinjëve të tjetrit. Këndet AOB dhe COD, BOD dhe AOC, të formuara në kryqëzimin e dy vijave të drejta, janë vertikale (Fig. 2).
Teorema 2. Këndet vertikale janë të barabarta.
Dëshmi. Le të shqyrtojmë kënde vertikale AOB dhe COD (shih Fig. 2). Këndi BOD është ngjitur me secilin nga këndet AOB dhe COD. Nga teorema 1 ∠ AOB + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Nga kjo arrijmë në përfundimin se ∠ AOB = ∠ COD.
Përfundim 1. Një kënd ngjitur me një kënd të drejtë është një kënd i drejtë.
Konsideroni dy drejtëza të kryqëzuara AC dhe BD (Fig. 3). Ata formojnë katër qoshe. Nëse njëri prej tyre është i drejtë (këndi 1 në figurën 3), atëherë këndet e mbetura janë gjithashtu të drejta (këndet 1 dhe 2, 1 dhe 4 janë ngjitur, këndet 1 dhe 3 janë vertikalë). Në këtë rast, ata thonë se këto drejtëza kryqëzohen në kënde të drejta dhe quhen pingul (ose reciprokisht pingul). Perpendikulariteti i drejtëzave AC dhe BD shënohet si më poshtë: AC ⊥ BD.
Një përgjysmues pingul me një segment është një drejtëz pingul me këtë segment dhe që kalon nga mesi i tij.
AN - pingul me një vijë
Konsideroni një drejtëz a dhe një pikë A të mos shtrirë mbi të (Fig. 4). Le të lidhim pikën A me një segment me pikën H me drejtëz a. Segmenti AN quhet pingul i tërhequr nga pika A në drejtëzën a nëse drejtëzat AN dhe a janë pingule. Pika H quhet baza e pingules.
Sheshi i vizatimit
Teorema e mëposhtme është e vërtetë.
Teorema 3. Nga çdo pikë që nuk shtrihet në një vijë, është e mundur të vizatoni një pingul me këtë drejtëz dhe, për më tepër, vetëm një.
Për të vizatuar një pingul nga një pikë në një vijë të drejtë në një vizatim, përdorni një katror vizatimi (Fig. 5).
Komentoni. Formulimi i teoremës zakonisht përbëhet nga dy pjesë. Një pjesë flet për atë që jepet. Kjo pjesë quhet kushti i teoremës. Pjesa tjetër flet për atë që duhet të vërtetohet. Kjo pjesë quhet përfundimi i teoremës. Për shembull, kushti i Teoremës 2 është që këndet të jenë vertikale; përfundim - këto kënde janë të barabarta.
Çdo teoremë mund të shprehet në detaje me fjalë në mënyrë që gjendja e saj të fillojë me fjalën "nëse" dhe përfundimi i saj me fjalën "atëherë". Për shembull, Teorema 2 mund të shprehet në detaje si më poshtë: "Nëse dy kënde janë vertikale, atëherë ato janë të barabarta."
Shembulli 1. Një nga këndet ngjitur është 44°. Me çfarë barazohet tjetri?
Zgjidhje.
Le të shënojmë masën e shkallës së një këndi tjetër me x, atëherë sipas teoremës 1.
44° + x = 180°.
Duke zgjidhur ekuacionin që rezulton, gjejmë se x = 136°. Prandaj, këndi tjetër është 136°.
Shembulli 2. Le të jetë këndi COD në figurën 21 45°. Cilat janë këndet AOB dhe AOC?
Zgjidhje.
Këndet COD dhe AOB janë vertikale, prandaj sipas teoremës 1.2 janë të barabartë, d.m.th. ∠ AOB = 45°. Këndi AOC është ngjitur me këndin COD, që do të thotë sipas Teoremës 1.
∠ AOC = 180° - ∠ COD = 180° - 45° = 135°.
Shembulli 3. Gjeni kënde ngjitur nëse njëri prej tyre është 3 herë më i madh se tjetri.
Zgjidhje.
Le të shënojmë masën e shkallës së këndit më të vogël me x. Pastaj masë shkallë këndi më i madh do të jetë 3x. Meqenëse shuma e këndeve ngjitur është e barabartë me 180° (teorema 1), atëherë x + 3x = 180°, prej nga x = 45°.
Kjo do të thotë se këndet ngjitur janë 45° dhe 135°.
Shembulli 4. Shuma e dy këndeve vertikale është 100°. Gjeni madhësinë e secilit prej katër këndeve.
Zgjidhje.
Le të plotësojë kushtet e problemit Figura 2. Këndet vertikale COD me AOB janë të barabarta (teorema 2), që do të thotë se edhe masat e shkallës së tyre janë të barabarta. Prandaj, ∠ COD = ∠ AOB = 50° (shuma e tyre sipas kushtit është 100°). Këndi BOD (gjithashtu këndi AOC) është ngjitur me këndin COD, dhe për këtë arsye, nga Teorema 1
∠ BOD = ∠ AOC = 180° - 50° = 130°.
Kënde ngjitur- dy kënde në të cilat njëra anë është e përbashkët dhe dy të tjerat janë vazhdimësi e njëra-tjetrës.
Shuma e këndeve ngjitur është 180°
Kënde vertikale- këto janë dy kënde në të cilat brinjët e njërit kënd janë vazhdimësi e brinjëve të tjetrit.
Këndet vertikale janë të barabarta.
2. Shenjat e barazisë së trekëndëshave:
firmos: Nëse dy brinjë dhe këndi ndërmjet tyre i një trekëndëshi janë përkatësisht të barabartë me dy brinjë dhe këndi ndërmjet tyre i një trekëndëshi tjetër, atëherë trekëndëshat e tillë janë kongruentë.
Shenja II: Nëse brinjët dhe dy këndet fqinjë të një trekëndëshi janë përkatësisht të barabarta me brinjën dhe dy këndet fqinjë të një trekëndëshi tjetër, atëherë trekëndëshat e tillë janë kongruentë.
Shenja III: Nëse tre brinjët e një trekëndëshi janë përkatësisht të barabarta me tre brinjët e një trekëndëshi tjetër, atëherë trekëndëshat e tillë janë kongruentë
3. Shenjat e paralelizmit të dy drejtëzave: kënde të njëanshme, të shtrira tërthore dhe përkatëse:
Dy rreshta në një rrafsh quhen paralele, nëse nuk kryqëzohen.
Kënde tërthore: 3 dhe 5, 4 dhe 6;
Kënde të njëanshme: 4 dhe 5, 3 dhe 6; oriz. Faqe 55
Këndet përkatëse: 1 dhe 5, 4 dhe 8, 2 dhe 6, 3 dhe 7;
Teorema: Nëse, kur dy drejtëza kryqëzohen me një tërthore, këndet e shtrira janë të barabarta, atëherë drejtëzat janë paralele.
Teorema: Nëse, kur dy drejtëza priten me një tërthore, këndet përkatëse janë të barabarta, atëherë drejtëzat janë paralele.
Teorema: Nëse, kur dy drejtëza priten me një tërthore, shuma e këndeve të njëanshme është 180°, atëherë drejtëzat janë paralele.
Teorema: nëse dy drejtëza paralele priten nga një transversal, atëherë këndet e prerjes janë të barabarta
Teorema: nëse dy drejtëza paralele priten nga një transversal, atëherë këndet përkatëse janë të barabarta
Teorema: nëse dy drejtëza paralele priten nga një transversal, atëherë shuma e këndeve të njëanshme është 180°
4. Shuma e këndeve të trekëndëshit:
Shuma e këndeve të një trekëndëshi është 180°
5. Vetitë e një trekëndëshi dykëndësh:
Teorema: Në një trekëndësh dykëndësh, këndet e bazës janë të barabarta.
Teorema: Në një trekëndësh dykëndësh, përgjysmuesja e tërhequr në bazë është mediana dhe lartësia (mesatarja është e kundërta), (përgjysmuesja përgjysmon këndin, mesatarja përgjysmon anën, lartësia formon një kënd prej 90°)
Shenja: Nëse dy kënde të një trekëndëshi janë të barabartë, atëherë trekëndëshi është dykëndësh.
6. Trekëndëshi kënddrejtë:
Trekëndësh kënddrejtë- është një trekëndësh në të cilin një kënd është i drejtë (pra 90 gradë)
Në një trekëndësh kënddrejtë, hipotenuza është më e gjatë se këmba
1. Shuma e dy këndeve akute trekëndësh kënddrejtë e barabartë me 90°
2. Një këmbë e një trekëndëshi kënddrejtë e shtrirë përballë një këndi prej 30° është e barabartë me gjysmën e hipotenuzës
3. Nëse një këmbë e një trekëndëshi kënddrejtë është e barabartë me gjysmën e hipotenuzës, atëherë këndi përballë kësaj kate është 30°
7. Trekëndësh barabrinjës:
TREKËNDËSH BABARAFINËS, një figurë e sheshtë që ka tre brinjë me gjatësi të barabartë; tre qoshet e brendshme, të formuara nga anët, janë gjithashtu të barabarta dhe arrijnë në 60 °C.
8. Sin, cos, tg, ctg:
Sin=, Cos=, tg=, ctg=, tg= ![]() ,ctg=
,ctg=
9. Shenjat e një katërkëndëshi^
Shuma e këndeve të një katërkëndëshi është 2 π = 360°.
Një katërkëndësh mund të futet në një rreth nëse dhe vetëm nëse shuma e këndeve të kundërta është 180°
10. Shenjat e ngjashmërisë së trekëndëshave:
firmos: nëse dy kënde të një trekëndëshi janë përkatësisht të barabartë me dy kënde të një tjetri, atëherë trekëndëshat e tillë janë të ngjashëm
Shenja II: Nëse dy brinjët e një trekëndëshi janë proporcionale me dy brinjët e një trekëndëshi tjetër dhe këndet ndërmjet këtyre brinjëve janë të barabartë, atëherë trekëndëshat e tillë janë të ngjashëm.
Shenja III: nëse tre brinjët e një trekëndëshi janë proporcionale me tre brinjët e një tjetri, atëherë trekëndëshat e tillë janë të ngjashëm
11. Formulat:
· Teorema e Pitagorës: a 2 +b 2 =c 2
· teorema e mëkatit: 
· teorema e cos: 
· 3 formula për sipërfaqen e një trekëndëshi: 
· Sipërfaqja e një trekëndëshi kënddrejtë: S= S=
· Sipërfaqja e një trekëndëshi barabrinjës:
· Sipërfaqja e një paralelogrami: S = ah
· Zona katrore: S = a2
· Zona e trapezit: 
· Zona e rombit:
· Zona drejtkëndëshe: S=ab
· Trekëndësh barabrinjës. Lartësia: h=
· Njësia trigonometrike: sin 2 a+cos 2 a=1
· vija e mesme trekëndësh: S=
· Vija e mesme e trapezit: MK=
©2015-2019 sajti
Të gjitha të drejtat u përkasin autorëve të tyre. Kjo faqe nuk pretendon autorësinë, por ofron përdorim falas.
Data e krijimit të faqes: 2017-12-12
E barabartë me dy kënde të drejta .
Jepen dy kënde ngjitur: AOB Dhe VOS. Kërkohet të vërtetohet se:
∠AOB+∠BOS=d+ d = 2d
Le të rikthehemi nga pika RRETH në një vijë të drejtë AC pingul O.D.. Këndin AOB e ndamë në dy pjesë AOD dhe DOB në mënyrë që të mund të shkruajmë:
∠AOB = ∠ A.O.D+∠ DO.B.
Le t'i shtojmë të dy anët e kësaj barazie të njëjtin kënd BOC, pse nuk do të cenohet barazia:
∠ A.O.B + ∠ B.O.ME= ∠AOD + ∠ DO.B. + ∠ B.O.ME
Që nga shuma DO.B. + BOC arrin në kënd i drejtë BËJME, Kjo
∠ A.O.B+ ∠ B.O.ME= ∠ A.O.D + ∠ BËJME= d + d = 2 d,
Q.E.D.
Pasojat.
1. Shuma e këndeve (A.O.B,BOC, SOD, DOE), i vendosur rreth një kulmi të përbashkët (O) në njërën anë të vijës së drejtë ( A.E.) është e barabartë me 2 d= 180 0 , sepse kjo shumë është shuma e dy qoshet ngjitur, për shembull këto: AOC + COE
2. Shuma e këndeve të vendosura rreth një të përbashkët majat (O) në të dy anët e çdo vije të drejtë është e barabartë me 4 d=360 0,
Teorema e bashkëbisedimit.
Nëse shuma e dy këndeve, duke pasur një kulm të përbashkët dhe një anë të përbashkët dhe që nuk mbulojnë njëra-tjetrën, është e barabartë me dy kënde të drejta (2d), atëherë kënde të tilla janë ngjitur, d.m.th. dy anët e tjera të tyre janë vijë e drejtë.
Nëse nga një pikë (O) e një drejtëze (AB) i rivendosim pingulet, në secilën anë, atëherë këto pingule formojnë një drejtëz (CD). Nga çdo pikë jashtë vijës mund të bini në këtë linjë pingul dhe vetëm një në atë.
Sepse shuma e këndeve COB Dhe BODështë e barabartë me 2d.
DrejtME pjesë të së cilës OME Dhe O.D. shërbejnë si pingul me një vijë AB, quhet drejtëz pingul me AB.
Nëse drejt MED pingul me vijën AB, pastaj anasjelltas: AB pingul me MED, sepse pjesët O.A. Dhe O.B. shërbejnë edhe pingul me MED. Prandaj drejt AB Dhe MED quhen pingul reciprokisht.
Ata të dy janë të drejtë AB Dhe MED reciprokisht pingul, e shprehur me shkrim si më poshtë AB^ MED.
Të dy këndet quhen vertikale, nëse anët e njërës janë vazhdimësi e brinjëve të tjetrës.
Pra, në kryqëzimin e dy linjave AB Dhe MED formohen dy palë kënde vertikale: A.O.D Dhe COB; AOC Dhe DO.B. .
Teorema.
Dy kënd vertikal të barabartë .
Le të jepen dy kënde vertikale: AOD Dhe MEO.B. ato. O.B. ka një vazhdim O.A., A OME vazhdimi O.D..
Kërkohet të vërtetohet se AOD = MEO.B.
Bazuar në vetinë e këndeve ngjitur, mund të shkruajmë:
A.O.D + DO.B.= 2 d
DOB + BOC = 2d
Do të thotë: AOD + DOB = DOB + BOC.
Nëse kësaj i zbresim të dyja anët barazisë sipas këndit DO.B., marrim:
A.O.D = BOC, që ishte ajo që duhej vërtetuar.
Në mënyrë të ngjashme do ta vërtetojmë këtë AOC = DO.B..
Në këtë mësim do të shikojmë dhe kuptojmë konceptin e këndeve ngjitur. Le të shqyrtojmë një teoremë që ka të bëjë me ta. Le të prezantojmë konceptin e "këndeve vertikale". Le të shohim disa fakte mbështetëse në lidhje me këto kënde. Më pas, ne formulojmë dhe vërtetojmë dy përfundime rreth këndit midis përgjysmuesve të këndeve vertikale. Në fund të mësimit do të shqyrtojmë disa probleme në këtë temë.
Le ta fillojmë mësimin tonë me konceptin e "këndeve ngjitur". Figura 1 tregon këndin e zhvilluar ∠AOC dhe rrezen OB, e cila e ndan këtë kënd në 2 kënde.
Oriz. 1. Këndi ∠AOC
Le të shqyrtojmë këndet ∠AOB dhe ∠BOC. Është mjaft e qartë se ata kanë një anë të përbashkët VO, dhe anët AO dhe OS janë të kundërta. Rrezet OA dhe OS plotësojnë njëra-tjetrën, që do të thotë se shtrihen në të njëjtën vijë të drejtë. Këndet ∠AOB dhe ∠BOC janë ngjitur.
Përkufizim: Nëse dy kënde kanë një anë të përbashkët, dhe dy brinjët e tjera janë rreze plotësuese, atëherë këto kënde quhen ngjitur.
Teorema 1: Shuma e këndeve ngjitur është 180 o.

Oriz. 2. Vizatim për teoremën 1
∠MOL + ∠LON = 180 o. Ky pohim është i vërtetë, pasi rrezja OL ndan këndin e shpalosur ∠MON në dy kënde ngjitur. Kjo do të thotë, ne nuk i dimë masat e shkallës së asnjë prej këndeve ngjitur, por dimë vetëm shumën e tyre - 180 gradë.
Konsideroni kryqëzimin e dy vijave. Figura tregon kryqëzimin e dy drejtëzave në pikën O.

Oriz. 3. Këndet vertikale ∠ВОА dhe ∠СOD
Përkufizim: Nëse brinjët e njërit kënd janë vazhdimësi e këndit të dytë, atëherë kënde të tilla quhen vertikale. Kjo është arsyeja pse figura tregon dy palë kënde vertikale: ∠AOB dhe ∠COD, si dhe ∠AOD dhe ∠BOC.
Teorema 2: Këndet vertikale janë të barabarta.
Le të përdorim figurën 3. Konsideroni këndin e rrotulluar ∠AOC. ∠AOB = ∠AOC - ∠BOC = 180 o - β. Le të shqyrtojmë këndin e rrotulluar ∠BOD. ∠COD = ∠BОD - ∠BOC = 180 o - β.
Nga këto konsiderata arrijmë në përfundimin se ∠AOB = ∠COD = α. Në mënyrë të ngjashme, ∠AOD = ∠BOS = β.
Përfundimi 1: Këndi ndërmjet përgjysmuesve të këndeve ngjitur është 90°.

Oriz. 4. Vizatim për përfundimin 1
Meqenëse OL është përgjysmues i këndit ∠BOA, atëherë këndi ∠LOB = , ngjashëm me ∠BOA = . ∠LOK = ∠LOB + ∠BOK = + = ![]() . Shuma e këndeve α + β është e barabartë me 180°, pasi këto kënde janë ngjitur.
. Shuma e këndeve α + β është e barabartë me 180°, pasi këto kënde janë ngjitur.
Përfundimi 2: Këndi ndërmjet përgjysmuesve të këndeve vertikale është i barabartë me 180°.

Oriz. 5. Vizatim për përfundimin 2
KO është përgjysmues ∠AOB, LO është përgjysmues ∠COD. Natyrisht, ∠KOL = ∠KOB + ∠BOC + ∠COL = o. Shuma e këndeve α + β është e barabartë me 180°, pasi këto kënde janë ngjitur.
Le të shohim disa detyra:
Gjeni këndin ngjitur me ∠AOC nëse ∠AOC = 111 o.
Le të bëjmë një vizatim për detyrën:

Oriz. 6. Vizatim për shembull 1
Meqenëse ∠AOC = β dhe ∠COD = α janë kënde ngjitur, atëherë α + β = 180 o. Kjo është, 111 o + β = 180 o.
Kjo do të thotë β = 69 o.
Ky lloj problemi shfrytëzon teoremën e shumës së këndeve ngjitur.
Një nga këndet ngjitur është një kënd i drejtë, cili është këndi tjetër (akut, i mpirë apo i drejtë)?
Nëse njëri prej këndeve është i drejtë, dhe shuma e dy këndeve është 180°, atëherë edhe këndi tjetër është i drejtë. Ky problem teston njohuritë për shumën e këndeve ngjitur.
A është e vërtetë që nëse këndet ngjitur janë të barabartë, atëherë ato janë kënde të drejta?
Le të bëjmë një ekuacion: α + β = 180 o, por meqë α = β, atëherë β + β = 180 o, që do të thotë β = 90 o.
Përgjigje: Po, pohimi është i vërtetë.
Janë dhënë dy kënde të barabarta. A është e vërtetë që edhe këndet ngjitur me to do të jenë të barabartë?

Oriz. 7. Vizatim për shembull 4
Nëse dy kënde janë të barabartë me α, atëherë këndet e tyre përkatëse ngjitur do të jenë 180 o - α. Kjo do të thotë, ata do të jenë të barabartë me njëri-tjetrin.
Përgjigje: Deklarata është e vërtetë.
- Alexandrov A.D., Werner A.L., Ryzhik V.I. dhe të tjera.Gjeometria 7. - M.: Edukimi.
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. dhe të tjera.Gjeometria 7. 5th ed. - M.: Iluminizmi.
- \Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Gjeometria 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, redaktuar nga V.A. Sadovnichigo. - M.: Arsimi, 2010.
- Matja e segmenteve ().
- Mësimi i përgjithshëm mbi gjeometrinë në klasën e 7-të ().
- Vijë e drejtë, segment ().
- Nr. 13, 14. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Gjeometria 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, redaktuar nga V.A. Sadovnichigo. - M.: Arsimi, 2010.
- Gjeni dy kënde ngjitur nëse njëri është 4 herë tjetri.
- Duke pasur parasysh këndin. Ndërtoni kënde ngjitur dhe vertikale për të. Sa kënde të tilla mund të ndërtohen?
- * Në cilin rast fitohen më shumë çifte këndesh vertikale: kur ndërpriten tri drejtëza në një pikë apo në tri pika?
me temë: Këndet fqinje dhe vertikale, vetitë e tyre.
(3 mësime)
Si rezultat i studimit të temës që ju nevojitet:
TE JESH I AFTE TE:Konceptet: kënde ngjitur dhe vertikale, vija pingule
Dalloni këndet ngjitur dhe vertikalë
Teorema e këndit fqinj dhe vertikal
Zgjidh problema duke përdorur vetitë e këndeve ngjitur dhe vertikal
Vetitë e këndeve ngjitur dhe vertikale
Ndërtoni kënde ngjitur dhe vertikale pingul me vijat e drejta
LITERATURA:
1. Gjeometria. klasa e 7-të. Zh. Kajdasov, G. Dosmagambetova, V. Abdiev. Almaty "Mektep". 2012
2. Gjeometria. klasa e 7-të. K.O.Bukubaeva, A.T. Mirazova. Almaty "Atamura" 2012
3. Gjeometria. klasa e 7-të. Manual metodik. K.O. Bukubaeva. Almaty "Atamura" 2012
4. Gjeometria. klasa e 7-të. Materiali didaktik. A.N. Shynybekov. Almaty "Atamura" 2012
5. Gjeometria. klasa e 7-të. Mbledhja e detyrave dhe ushtrimeve. K.O. Bukubaeva, A.T. Mirazova. Almaty "Atamura" 2012
Mos harroni se duhet të punoni sipas algoritmit!
Mos harroni të kontrolloni, bëni shënime në margjina,
Ju lutemi mos lini asnjë pyetje që keni pa përgjigje.
Tregohuni objektiv gjatë verifikimit të ndërsjellë, do t'ju ndihmojë edhe juve edhe personit
kë po kontrollon
JU UROJ SUKSES!
DETYRA Nr. 1.
Lexoni përkufizimin dhe mësoni (2b):
Përkufizimi. Këndet në të cilat njëra anë është e përbashkët dhe dy anët e tjera janë rreze shtesë quhen fqinjë.
2) Mësoni dhe shkruani teoremën në fletoren tuaj: (2b)
Shuma e këndeve ngjitur është 180.
E dhënë:∠ ANM dhe∠ DOV – të dhënat e këndeve ngjitur
OD - anë e përbashkët
Provoj:
∠ AOD +∠ DOV = 180
Dëshmi:

Bazuar në aksiomënIII 4:
∠ AOD +∠ DOV =∠ AOB.
∠ AOB - i zgjeruar. Prandaj,
∠ AOD +∠ DOV = 180
Teorema është vërtetuar.
3) Nga teorema rrjedh: (2b)
1) Nëse dy kënde janë të barabarta, atëherë këndet e tyre ngjitur janë të barabartë;
2) nëse këndet ngjitur janë të barabartë, atëherë masa e shkallës së secilit prej tyre është 90°.
Mbani mend!
Një kënd i barabartë me 90° quhet kënd i drejtë.
Një kënd më i vogël se 90° quhet kënd akut.
Një kënd më i madh se 90° dhe më i vogël se 180° quhet kënd i mpirë.

Këndi i drejtë Këndi i mprehtë Këndi i mpirë
Meqenëse shuma e këndeve ngjitur është 180°, atëherë
1) një kënd ngjitur me një kënd të drejtë, i drejtë;
2) këndi ngjitur me këndin akut është i mpirë;
3) një kënd ngjitur me një kënd të mpirë është akut.
4) Konsideroni një zgjidhje mostëradachi:
a) Duke pasur parasysh:∠ hkDhe∠ kl- ngjitur;∠ hkmë shumë∠ klnë 50°.
Gjej:∠ hkDhe∠ kl.

Zgjidhja: Le∠ kl= x, atëherë∠ hk= x + 50°. Nga vetia e shumës së këndeve ngjitur∠ kl + ∠ hk= 180°.
x + x + 50° = 180°;
2x = 180° - 50°;
2x = 130°;
x = 65°.
∠ kl= 65°;∠ hk= 65°+ 50° = 115°.
Përgjigje: 115° dhe 65°.
b) Le∠ kl= x, atëherë∠ hk= 3x
x + 3x = 180°; 4x = 180°; x = 45°;∠ kl= 45°;∠ hk= 135°.
Përgjigje: 135° dhe 45°.
5) Puna me përcaktimin e këndeve ngjitur: (2 b)
6) Gjeni gabime në përkufizime: (2b)

Kaloni testin numër 1
Detyra nr. 2
1) Ndërtoni 2 kënde ngjitur në mënyrë që ana e tyre e përbashkët të kalojë përmes pikës C dhe brinja e njërit prej këndeve të përputhet me rrezen AB. (2b)
2). Punë praktike për të zbuluar vetitë e këndeve ngjitur: (5b)
Përparim
1. Ndërtoni një këndkëndi ngjiturA , NëseA : i mprehtë, i drejtë, i hapur.
2. Matni këndet.
3. Futni të dhënat e matjes në tabelë.
4. Gjeni marrëdhënien ndërmjet këndeveA Dhe.
5. Nxirrni një përfundim për vetinë e këndeve fqinjë.
Kaloni testin numër 2
Detyra nr. 3
Vizatoni të pazgjeruarin∠ AOB dhe emërtoni rrezet që janë brinjët e këtij këndi.
Vizatoni rreze O, e cila është vazhdimësi e rrezes OA, dhe rreze OD, e cila është vazhdimësi e rrezes OB.
Shkruani në fletore: kënde∠ AOB dhe∠ SOD quhen vertikale. (3b)
Mësoni dhe shkruani në fletoren tuaj: (4b)
Përkufizimi: Quhen kënde në të cilat brinjët e njërës prej tyre janë rreze plotësuese të tjetrësqoshet vertikale.

< 1 dhe<2, <3 и <4 kënde vertikale
RrezetOFDheO.A. , O.C.DheO.E.janë rreze komplementare në çift.
Teorema: Këndet vertikale janë të barabarta.
Dëshmi.

Këndet vertikale formohen kur kryqëzohen dy drejtëza. Lërini vijat e drejta a dhebkryqëzohen në pikën O.∠ 1 dhe∠ 2 – kënde vertikale.
∠ AOC-zgjeruar, që do të thotë∠ AOC = 180°. Megjithatë∠ 1+ ∠ 2= ∠ AOC, d.m.th.
∠ 3+ ∠ 1= 180°, nga këtu kemi:
∠ 1= 180 - ∠ 3. (1)
Ne gjithashtu kemi atë∠ DOV = 180°, nga këtu∠ 2+ ∠ 3= 180° ose∠ 2= 180°- ∠ 3. (2)
Meqenëse në barazitë (1) dhe (2) pjesët e drejta janë të barabarta, atëherë∠ 1= ∠ 2.
Teorema është vërtetuar.
5). Puna me përcaktimin e këndeve vertikale: (2b)

6) Gjeni gabimin në përkufizim: (2b).

Kaloni testin numër 3
Detyra nr 4
1) Punë praktike për zbulimin e vetive të këndeve vertikale: (5b)
Progresi:
1. Ndërtoni këndin β kënd vertikalα , Nëseα :
i mprehtë, i drejtë, i hapur.
2.Masni këndet.
3. Futni të dhënat e matjes në tabelë
4. Gjeni marrëdhënien ndërmjet këndeve α dhe β.
5.Nxirrni një përfundim për vetitë e këndeve vertikale.
2) Vërtetimi i vetive të këndeve ngjitur dhe vertikal. (3b)
2) Konsideroni një zgjidhje mostëradachi.
Detyrë. Drejtëzat AB dhe CD priten në pikën O në mënyrë që∠ AOD = 35°. Gjeni këndet AOC dhe BOC.

Zgjidhja:
1) Prandaj, këndet AOD dhe AOS janë ngjitur∠ BOC= 180° - 35° = 145°.
2) Këndet AOC dhe BOC janë gjithashtu ngjitur, prandaj∠ BOC= 180° - 145° = 35°.
Do të thotë,∠ BOC = ∠ AOD = 35°, dhe këto kënde janë vertikale. Pyetje: A është e vërtetë që të gjitha këndet vertikale janë të barabarta?
3) Zgjidhja e problemeve në vizatimet e përfunduara: (3b)
1. Gjeni këndet AOB, AOD, COD.


3) Gjeni këndet BOC, FOA.: (3b)

3. Gjeni në figurë këndet fqinje dhe vertikale. Le të dihen vlerat e dy këndeve të shënuara në vizatim, 28? dhe 90?. A është e mundur të gjenden vlerat e këndeve të mbetura pa kryer matje (2b)
Kaloni testin numër 4
Detyra nr 5
Testoni njohuritë tuaja duke plotësuarPuna testuese nr. 1
Detyra nr. 6
1) Provoni vetitë e këndeve vertikale dhe shkruani këto prova në fletoren tuaj. (3b)
Nxënësit në mënyrë të pavarur, duke përdorur vetitë e këndeve vertikale dhe të afërta, duhet të arsyetojnë faktin se nëse, kur dy drejtëza kryqëzohen, njëri nga këndet që rezulton është drejtëz, atëherë edhe këndet e mbetura janë kënde të drejta.
2) Zgjidh dy probleme për të zgjedhur:
1. Masat e shkallës së këndeve ngjitur janë në raport 7:2. Gjeni këto kënde. (2b)
2. Njëri nga këndet e formuar kur kryqëzohen dy drejtëza është 11 herë më i vogël se tjetri Gjeni secilin nga këndet (3b)
3. Gjeni kënde ngjitur nëse ndryshimi dhe shuma e tyre janë në raportin 2:9. (3b)
Detyra nr 7
Te lumte! Mund të filloni punën testuese nr. 2.
Puna testuese nr. 1.
Vendosni të zgjidhni ndonjë nga opsionet (10b)
opsioni 1
<1 и <2,<3 и <2,
G)<1 и <3. Какие это углы?
Të lidhura
e) Vizatoni (me sy) një kënd prej 30° dhe< ABC, ngjitur me atë të dhënë

f) Cilat kënde quhen vertikale?
Dy kënde quhen vertikale nëse janë të barabartë.
g) Nga pika A vizatoni dy drejtëza pingul me drejtëzënA
Mund të vizatoni vetëm një vijë të drejtë.

Opsioni 2
1. Nxënësi, duke iu përgjigjur pyetjeve të mësuesit, dha përgjigjet e duhura. Kontrolloni nëse janë të sakta duke shënuar fjalët "PO", "JO", "NUK E DI" në kolonën e tretë. Nëse "JO", shkruani përgjigjen e saktë atje ose shtoni atë që mungon.
<1 и <4,<2 и <4
D)<1 и < 3 смежные?
Nr. Ato janë vertikale
E) Cilat drejtëza quhen pingule?
Dy drejtëza quhen pingul nëse priten në kënde të drejta
G) Vizatoni kënde vertikale në mënyrë që anët e tyre të jenë pingul me vijat e drejta.

2. Emërtoni këndet vertikale në këtë figurë.

Gjithsej: 10 pikë
“5” -10 pikë;
“4” -8-9 pikë;
"3" -5-7 pikë.
Puna testuese nr. 2.
Vendosni të zgjidhni ndonjë opsion
Opsioni I
Gjeni kënde të afërta nëse ndryshimi dhe shuma e tyre janë në raport 2:9. (4b)
Gjeni të gjitha këndet e formuara nga kryqëzimi i dy drejtëzave nëse njëra prej tyre është 240° më e vogël se shuma e dy të tjerave. (6b)
Opsioni II
1) Gjeni kënde ngjitur nëse ndryshimi dhe shuma e tyre janë në raportin 5:8(4b)
2) Gjeni të gjitha këndet e pazhvilluara të formuara në kryqëzimin e dy drejtëzave, nëse njëra prej tyre është 60° më e madhe se shuma e dy të tjerave. (6b)
Gjithsej: 10 pikë
“5” -10 pikë;
“4” -8-9 pikë;
"3" -5-7 pikë.
