¿Estás aquí ahora? =) No, no intenté intimidar a nadie, es solo que el tema de las integrales impropias es una muy buena ilustración de lo importante que es no ejecutar matemáticas superiores y demás. Ciencias Exactas. Para dominar la lección en el sitio, todo está allí, en detalle y forma accesible, habría un deseo ....
Entonces, comencemos. Hablando en sentido figurado, integral impropia es una integral definida "avanzada", y de hecho no hay tantas dificultades con ellos, además, la integral impropia tiene un significado geométrico muy bueno.
¿Qué significa calcular una integral impropia?
Calcular integral impropia - significa encontrar un NÚMERO(exactamente lo mismo que en la integral definida), o probar que diverge(es decir, terminar con infinito en lugar de un número).
Las integrales impropias son de dos tipos.
Integral impropia con límite(s) infinito(s) de integración
A veces, una integral impropia de este tipo se llama integral impropia de primera clase. EN vista general Una integral impropia con un límite infinito suele verse así: . ¿En qué se diferencia de una integral definida? En el límite superior. es interminable:
Menos comunes son las integrales con un límite inferior infinito o con dos límites infinitos: , y las consideraremos más adelante, cuando pruebes :)
Bueno, ahora analicemos el caso más popular. En la gran mayoría de los ejemplos, la función integrando continuo en medio y este hecho importante para comprobar primero! Porque si hay lagunas, entonces hay matices adicionales. Para mayor precisión, asumimos que incluso entonces el típico trapecio curvilíneo se verá así:
Note que es infinito (no acotado por la derecha), y integral impropia numéricamente igual a su área. En este caso, las siguientes opciones son posibles:
1) El primer pensamiento que viene a la mente es: “ya que la figura es infinita, entonces 
”, en otras palabras, el área también es infinita. Entonces puede ser. En este caso, decimos que la integral impropia diverge.
2) Pero. Por paradójico que parezca, el área de una figura infinita puede ser igual a… ¡un número finito! Por ejemplo: . ¿Podría ser? Fácil. En el segundo caso, la integral impropia converge.
3) Sobre la tercera opción un poco más adelante.
¿Cuándo diverge y cuándo converge una integral impropia? Depende del integrando y ejemplos concretos vamos a revisar muy pronto.
Pero, ¿qué sucede si debajo del eje se ubica un trapezoide curvilíneo infinito? En este caso, la integral impropia 
(diverge) o igual a la final numero negativo.
De este modo, integral impropia puede ser negativa.
¡Importante! Cuando se le ofrece CUALQUIER integral impropia para resolver, entonces, en términos generales, no se habla de ninguna zona y no hay necesidad de construir un dibujo. Dije el significado geométrico de la integral impropia solo para que sea más fácil de entender el material.
Dado que la integral impropia es muy similar a la integral definida, recordamos la fórmula de Newton-Leibniz: 
. De hecho, la fórmula también es aplicable a integrales impropias, solo que debe modificarse ligeramente. ¿Cuál es la diferencia? En el límite superior infinito de integración: . Probablemente, muchos habrán adivinado que esto ya huele a aplicar la teoría de los límites, y la fórmula quedará escrita de la siguiente manera: 
.
¿En qué se diferencia de una integral definida? ¡Sí, nada especial! Como en una integral definida, debe poder encontrar la función antiderivada (integral indefinida), poder aplicar la fórmula de Newton-Leibniz. Lo único que se ha añadido es el cálculo del límite. Quien es malo con ellos, aprende una lección Límites de funciones. Ejemplos de solución porque mejor tarde que en el ejercito.
Considere dos ejemplos clásicos:
Ejemplo 1
Para mayor claridad, construiré un dibujo, aunque, recalco una vez más, en la práctica no es necesario construir dibujos en esta tarea.
El integrando es continuo en el medio intervalo, lo que significa que todo está bien y la integral impropia se puede calcular usando el método "regular".
Aplicación de nuestra fórmula 
y la solución se ve así:
Es decir, la integral impropia diverge y el área del trapezoide curvilíneo sombreado es igual a infinito.
En el ejemplo considerado, tenemos la integral tabular más simple y la misma técnica para aplicar la fórmula de Newton-Leibniz que en la integral definida. Pero esta fórmula se aplica bajo el signo del límite. En lugar de la letra habitual de la variable "dinámica", aparece la letra "ser". Esto no debe confundir ni confundir, porque cualquier letra no es peor que la "X" estándar.
Si no entiende por qué en , entonces esto es muy malo, o no entiende los límites más simples (y no entiende en absoluto qué es un límite), o no sabe cómo se ve el gráfico función logarítmica. En el segundo caso, visita la lección. Gráficas y propiedades de funciones elementales.
¡Al resolver integrales impropias, es muy importante saber cómo se ven los gráficos de las principales funciones elementales!
Un diseño de trabajo limpio debería verse así:
“
! Al diseñar un ejemplo, siempre interrumpimos la solución e indicamos qué sucede con el integrando – ¿Es continua en el intervalo de integración o no?. Con esto identificamos el tipo de integral impropia y fundamentamos otras acciones.
Ejemplo 2
Calcular la integral impropia o establecer su divergencia.
Hagamos un dibujo: 
Primero, notamos lo siguiente: el integrando es continuo en el semiintervalo. Bueno. Resolviendo con formula 
:
(1) Tomamos la integral más simple de función de poder(este caso particular se encuentra en muchas tablas). Es mejor mover inmediatamente el signo menos más allá del signo de límite para que no se interponga en los cálculos posteriores.
(2) Sustituimos los límites superior e inferior según la fórmula de Newton-Leibniz.
(3) Indicamos que cuando (Señores, esto se ha entendido desde hace mucho tiempo) y simplificamos la respuesta.
¡Aquí, el área de un trapezoide curvilíneo infinito es igual a un número finito! Increíble pero cierto.
El diseño limpio del ejemplo debería verse así:
“
El integrando es continuo en
“
Qué hacer si te encuentras con una integral como - con punto de ruptura en el intervalo de integración? Esto significa que hay un error tipográfico en el ejemplo. (Más probable) o un nivel avanzado de educación. En este último caso, debido a propiedades de aditividad, uno debe considerar dos integrales impropias en los intervalos y luego tratar con la suma.
A veces, debido a un error tipográfico o a la intención de una integral impropia, puede no existe en absoluto, así, por ejemplo, si ponemos en el denominador de la integral anterior Raíz cuadrada de "x", entonces parte del intervalo de integración no entrará en absoluto en el dominio de definición del integrando.
Además, una integral impropia puede no existir incluso con todo el "bienestar aparente". Ejemplo clásico: . A pesar de la definición y continuidad del coseno, ¡tal integral impropia no existe! ¿Por qué? Es muy sencillo porque:
- no existe límite correspondiente.
¡Y tales ejemplos, aunque raros, se encuentran en la práctica! Así, además de la convergencia y la divergencia, también hay un tercer resultado de la solución con una respuesta completa: "no hay integral impropia".
También se debe tener en cuenta que una definición rigurosa de integral impropia se da precisamente a través del límite, y aquellos que lo deseen pueden familiarizarse con él en la literatura educativa. bueno continuamos lección práctica y pasar a tareas más significativas:
Ejemplo 3
Calcular la integral impropia o establecer su divergencia.
Primero, tratemos de encontrar la función antiderivada (integral indefinida). Si fallamos en hacer esto, naturalmente tampoco resolveremos la integral impropia.
¿A cuál de las integrales de tabla se parece el integrando? Me recuerda al arco tangente: 
. A partir de estas consideraciones, se sugiere que sería bueno obtener un cuadrado en el denominador. Esto se hace por sustitución.
Reemplacemos:
Se ha encontrado la integral indefinida, no tiene sentido agregar una constante en este caso.
Sobre un borrador, siempre es útil realizar una comprobación, es decir, diferenciar el resultado:
Se obtuvo el integrando original, lo que significa que la integral indefinida se encontró correctamente.
Ahora encontramos la integral impropia:
(1) Escribimos la solución de acuerdo con la fórmula 
. Es mejor mover inmediatamente la constante más allá del signo del límite para que no interfiera en los cálculos posteriores.
(2) Sustituimos los límites superior e inferior de acuerdo con la fórmula de Newton-Leibniz. Por qué 
en ? Ver el gráfico de arco tangente en el artículo ya recomendado en repetidas ocasiones.
(3) Obtenemos la respuesta final. El hecho de que es útil saber de memoria.
Es posible que los estudiantes avanzados no encuentren la integral indefinida por separado y no usen el método de reemplazo, sino que usen el método de sumar la función bajo el signo diferencial y resuelvan la integral impropia "inmediatamente". En este caso, la solución debería ser algo como esto:
“
El integrando es continuo en . 
“
Ejemplo 4
Calcular la integral impropia o establecer su divergencia.
! Este es un ejemplo típico, y las integrales similares son muy comunes. ¡Hazlo bien! función antiderivada aquí está el método de selección cuadrado completo, se pueden encontrar más detalles sobre el método en la lección Integración de algunas fracciones.
Ejemplo 5
Calcular la integral impropia o establecer su divergencia.
Esta integral se puede resolver en detalle, es decir, primero encuentra la integral indefinida cambiando la variable. Y puede resolverlo "inmediatamente", sumando la función bajo el signo del diferencial. Quién tiene alguna base matemática.
Soluciones y respuestas completas al final de la lección.
En la página se pueden encontrar ejemplos de soluciones de integrales impropias con un límite inferior infinito de integración Métodos eficientes para resolver integrales impropias. Allí también se considera el caso en que ambos límites de integración son infinitos.
Integrales impropias de funciones ilimitadas
O integrales impropias de segunda clase. Las integrales impropias del segundo tipo se "cifran" astutamente bajo la integral definida habitual y se ven exactamente iguales: pero, a diferencia de la integral definida, el integrando sufre una discontinuidad infinita (no existe): 1) en el punto , 2) o en el punto , 3) o en ambos puntos a la vez, 4) o incluso en el intervalo de integración. Consideraremos los dos primeros casos, para los casos 3-4 al final del artículo hay un enlace a una lección adicional.
Solo un ejemplo para que quede claro:. Parece ser una integral definida. Pero, de hecho, esta es una integral impropia del segundo tipo, si sustituimos el valor del límite inferior en el integrando, entonces el denominador desaparece, es decir, ¡el integrando simplemente no existe en este punto!
En general, al analizar la integral impropia siempre es necesario sustituir ambos límites de integración en el integrando. En este sentido, también comprobamos el límite superior: 
. Todo es bueno aquí.
El trapezoide curvilíneo para la variedad considerada de la integral impropia fundamentalmente se ve así:
Aquí casi todo es igual que en la integral de primera clase.
Nuestra integral es numéricamente igual al área del trapezoide curvilíneo sombreado, que no está acotado desde arriba. En este caso, puede haber dos opciones*: la integral impropia diverge (el área es infinita) o la integral impropia es igual a un número finito (es decir, ¡el área de una figura infinita es finita!).
* por defecto, habitualmente asumimos que existe la integral impropia
Solo queda modificar la fórmula de Newton-Leibniz. También se modifica con la ayuda del límite, pero el límite ya no tiende al infinito, sino al valor de la derecha. Es fácil de seguir a lo largo del dibujo: a lo largo del eje, debemos acercarnos al punto de ruptura infinitamente cerca a la derecha.
Veamos cómo se implementa esto en la práctica.
Ejemplo 6
Calcular la integral impropia o establecer su divergencia.
El integrando sufre una ruptura infinita en un punto (¡no olvides verificar verbalmente o en un borrador si todo está bien con el límite superior!)
Primero, calculamos la integral indefinida: 
Reemplazo: 
Para aquellos que tienen dificultad con el reemplazo, consulte la lección Método de reemplazo en integral indefinida.
Calculamos la integral impropia:
(1) ¿Qué hay de nuevo aquí? Prácticamente nada en cuanto a técnica. Lo único que ha cambiado es la entrada bajo el icono de límite: . La adición significa que apuntamos al valor de la derecha (lo cual es lógico, vea el gráfico). Tal límite en la teoría de los límites se llama límite unilateral. En este caso tenemos límite de la derecha.
(2) Sustituimos los límites superior e inferior según la fórmula de Newton-Leibniz.
(3) Tratando con . ¿Cómo se determina hacia dónde se dirige una expresión? En términos generales, solo necesita sustituir el valor en él, sustituir tres cuartos e indicar eso. Peinando la respuesta.
En este caso, la integral impropia es igual a un número negativo. No hay delito en esto, solo el trapezoide curvilíneo correspondiente se encuentra debajo del eje.
Y ahora dos ejemplos para una decisión independiente.
Ejemplo 7
Calcular la integral impropia o establecer su divergencia.
Ejemplo 8
Calcular la integral impropia o establecer su divergencia.
Si el integrando no existe en el punto
Un trapezoide curvilíneo infinito para tal integral impropia básicamente se ve así.
Integral definida como límite de la suma integral
puede existir (es decir, tener un cierto valor final) solo si se cumplen las condiciones
Si se viola al menos una de estas condiciones, entonces la definición pierde su significado. De hecho, en el caso de un segmento infinito, por ejemplo [ a; ) no se puede descomponer en PAGS partes de longitud finita 
, que, además, tendería a cero con un aumento en el número de segmentos. En el caso de ilimitado en algún punto desde[a;
B] se viola el requisito de una elección arbitraria de un punto 
en segmentos parciales: no se puede seleccionar 
=desde, ya que el valor de la función en este punto no está definido. Sin embargo, la noción de integral definida también se puede generalizar para estos casos introduciendo un paso más al límite. Las integrales sobre intervalos infinitos y de funciones discontinuas (no acotadas) se llaman no propio.
Definición.
Deja que la función 
definido en el intervalo [ a; ) y es integrable en cualquier intervalo finito [ a;
B], es decir. existe 
para cualquiera B
> a. ver límite 
llamado integral impropia
primer tipo
(o por una integral impropia en un intervalo infinito) y denotamos 
.
Así, por definición, 
=
.
Si el límite por la derecha existe y es finito, entonces la integral impropia 
llamado convergente
. Si este límite es infinito, o no existe en absoluto, entonces se dice que la integral impropia es diverge
.
De manera similar, podemos introducir el concepto de integral impropia de una función 
por intervalo (–; B]:
=
.
Y la integral impropia de la función 
sobre el intervalo (–; +) se define como la suma de las integrales presentadas anteriormente:
=
+
,
donde pero es un punto arbitrario. Esta integral converge si ambos términos convergen y diverge si al menos uno de los términos diverge.
Desde un punto de vista geométrico, la integral 
,
, determina el valor numérico del área de un trapezoide curvilíneo infinito acotado superiormente por la gráfica de la función 
, izquierda - recto 
, desde abajo - el eje OX. La convergencia de la integral significa la existencia de un área finita de tal trapecio y su igualdad al límite del área de un trapezoide curvilíneo con una pared derecha móvil 
.
Para el caso de una integral con un límite infinito, también se puede generalizar Fórmula de Newton-Leibniz:
=
=F( +
) – F( a),
donde F( +
)
=
. Si existe este límite, entonces la integral converge; de lo contrario, diverge.
Hemos considerado una generalización del concepto de integral definida al caso de un intervalo infinito.
Consideremos ahora una generalización para el caso de una función ilimitada.
Definición
Deja que la función 
definido en el intervalo [ a;
B), no está acotado en alguna vecindad del punto B, y es continua en cualquier segmento 
, donde >0 (y, por lo tanto, es integrable en este segmento, es decir, 
existe). ver límite 
llamado integral impropia de segunda clase
(o por la integral impropia de una función ilimitada) y se denota 
.
Así, la integral impropia de ilimitada en un punto B Las funciones son por definición
=
.
Si el límite por la derecha existe y es finito, entonces la integral se llama convergente. Si no hay límite finito, entonces la integral impropia se llama divergente.
De manera similar, se puede definir una integral impropia de la función 
que tiene una discontinuidad infinita en un punto pero:
=
.
Si la función 
tiene una discontinuidad infinita en un punto interior desde
, entonces la integral impropia se define como sigue
=
+
=
+
.
Esta integral converge si ambos términos convergen y diverge si al menos un término diverge.
Desde un punto de vista geométrico, la integral impropia de una función ilimitada también caracteriza el área de un trapezoide curvilíneo ilimitado:
Dado que la integral impropia se deriva pasando al límite de la integral definida, entonces todas las propiedades de la integral definida pueden transferirse (con los refinamientos apropiados) a las integrales impropias de primera y segunda clase.
En muchos problemas que conducen a integrales impropias, no es necesario saber a qué es igual esta integral, basta con asegurarse de que converge o diverge. Para este uso signos de convergencia. Signos de convergencia de integrales impropias:
1) Signo de comparación.
Deja para todos X
. Entonces sí 
converge, luego converge y 
, y 
. Si 
diverge, luego diverge y 
.
2) Si converge 
, luego converge y 
(la última integral en este caso se llama absolutamente convergente).
Los criterios de convergencia y divergencia de integrales impropias de funciones ilimitadas son similares a los formulados anteriormente.
Ejemplos de resolución de problemas.
Ejemplo 1
pero) 
; B) 
; en) 
GRAMO) 
; mi) 
.
Solución.
a) Por definición tenemos:
.
b) Del mismo modo
Por lo tanto, esta integral converge y es igual a 
.
c) Por definición 
=
+
, es más, pero es un número arbitrario. Pongamos en nuestro caso 
, entonces obtenemos:
Esta integral converge.
Entonces esta integral diverge.
e) Considere 
. Para encontrar la antiderivada del integrando, es necesario aplicar el método de integración por partes. Entonces obtenemos:
ya que tampoco 
, ni 
no existen, entonces no existen y
Por lo tanto, esta integral diverge.
Ejemplo 2
Investigar la convergencia de la integral 
dependiendo de PAGS.
Solución.
En 
tenemos:
Si 
, luego 
Y. Por lo tanto, la integral diverge.
Si 
, luego 
, pero 
, luego
=,
Por lo tanto, la integral converge.
Si 
, luego
por lo tanto, la integral diverge.
De este modo, 
Ejemplo 3
Calcular la integral impropia o establecer su divergencia:
pero) 
; B) 
; en) 
.
Solución.
a) Integrales 
es una integral impropia de la segunda clase, porque el integrando 
no limitado en un punto 
. Entonces, por definición,
.
La integral converge y es igual a 
.
b) Considere 
. Aquí, también, el integrando no está acotado en el punto 
. Por tanto, esta integral es impropia de segunda clase y, por definición,
Por lo tanto, la integral diverge.
c) Considere 
. integrando 
sufre una discontinuidad infinita en dos puntos: 
Y 
, el primero de los cuales pertenece al intervalo de integración 
. Por tanto, esta integral es impropia de segunda clase. Entonces, por definición
=
=
.
Por lo tanto, la integral converge y es igual a 
.
Integral definida
\[I=\int_a^bf(x)dx\]
se construyó bajo el supuesto de que los números $a,\,b$ son finitos y $f(x)$ es una función continua. Si se viola una de estas suposiciones, se habla de integrales impropias.
10.1 Integrales impropias de primera clase
Una integral impropia del primer tipo surge cuando al menos uno de los números $a,\,b$ es infinito.
10.1.1 Definición y propiedades básicas
Consideremos primero la situación en la que el límite inferior de integración es finito y el límite superior es igual a $+\infty$; más adelante se discutirán otras opciones. Para $f(x)$ continua para todos los $x$ que nos interesen, considere la integral
\begin(ecuación) I=\int _a^(+\infty)f(x)dx. \quad(19) \label(inf1) \end(ecuación)
En primer lugar, es necesario establecer el significado de esta expresión. Para ello introducimos la función
\[ I(N)=\int _a^(N)f(x)dx \]
y considere su comportamiento como $N\rightarrow +\infty$.
Definición. Que haya un límite
\[ A=\lim_(N \rightarrow +\infty)I(N)=\lim_(N \rightarrow +\infty)\int _a^(N)f(x)dx. \]
Entonces se dice que la integral impropia de 1ra especie (19) es convergente y se le asigna el valor $A$, la función misma se llama integrable en el intervalo $\left[ a, \, +\infty \right) PS Si el límite indicado no existe o es igual a $\pm \infty$, entonces se dice que la integral (19) diverge.
Considere la integral
\[ I=\int _0^(+\infty) \frac(dx)(1+x^2). \]
\[ I(N)=\int _0^(N) \frac(dx)(1+x^2). \]
En este caso, se conoce la antiderivada del integrando, por lo que
\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)=arctgx|_0^(N)=arctgN. \]
Se sabe que $arctg N \rightarrow \pi /2 $ para $N \rightarrow +\infty$. Por lo tanto, $I(N)$ tiene un límite finito, nuestra integral impropia converge y es igual a $\pi /2$.
Las integrales impropias convergentes del primer tipo tienen todas las propiedades estándar de las integrales definidas ordinarias.
1. Si $f(x)$, $g(x)$ son integrables en el intervalo $\left[ a, \, +\infty \right)$, entonces su suma $f(x)+g(x) $ también es integrable en este intervalo, y \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx. \] 2. Si $f(x)$ es integrable en el intervalo $\left[ a, \, +\infty \right)$, entonces para cualquier constante $C$ la función $C\cdot f(x)$ también es integrable en este intervalo, y \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx. \] 3. Si $f(x)$ es integrable en el intervalo $\left[ a, \, +\infty \right)$ y $f(x)>0$ en este intervalo, entonces \[ \int _a ^ (+\infty) f(x)dx\,>\,0. \] 4. Si $f(x)$ es integrable en el intervalo $\left[ a, \, +\infty \right)$, entonces para cualquier $b>a$ la integral \[ \int _b^(+ \infty) f(x)dx \] converge, y \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty ) f( x)dx \] (aditividad de la integral sobre el intervalo).
Las fórmulas de cambio de variable, integración por partes, etc., también son válidas. (con reservas naturales).
Considere la integral
\begin(ecuación) I=\int _1^(+\infty)\frac(1)(x^k)\,dx. \quad (20) \label(mod) \end(ecuación)
Introducimos la función
\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx. \]
En este caso, la antiderivada es conocida, por lo que
\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k)|_1^N = \frac(N^(1-k))(1-k)-\frac(1)(1-k) \]
por $k \neq 1$,
\[ I(N)=\int _1^(N)\frac(1)(x)\,dx\,=lnx|_1^N= lnN \]
para $k = 1$. Considerando el comportamiento para $N \rightarrow +\infty$, llegamos a la conclusión de que la integral (20) converge para $k>1$, y diverge para $k \leq 1$.
Consideremos ahora el caso en que el límite inferior de integración es igual a $-\infty$ y el superior es finito, es decir considerar las integrales
\[ I=\int _(-\infty)^af(x)dx. \]
Sin embargo, esta variante se puede reducir a la anterior si hacemos el cambio de variables $x=-s$ y luego permutamos los límites de integración, de manera que
\[ I=\int _(-a)^(+\infty)g(s)ds, \]
$g(s)=f(-s)$. Consideremos ahora el caso cuando hay dos límites infinitos, es decir integral
\begin(ecuación) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(ecuación)
donde $f(x)$ es continua para todo $x \in \mathbb(R)$. Dividamos el intervalo en dos partes: tomemos $c \in \mathbb(R)$ y consideremos dos integrales,
\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx. \]
Definición. Si ambas integrales $I_1$, $I_2$ convergen, entonces la integral (21) se llama convergente, se le asigna el valor $I=I_1+I_2$ (según la aditividad del intervalo). Si al menos una de las integrales $I_1$, $I_2$ diverge, se dice que la integral (21) es divergente.
Se puede probar que la convergencia de la integral (21) no depende de la elección del punto $c$.
Las integrales impropias del primer tipo con intervalos de integración $\left(-\infty, \, c \right]$ o $(-\infty, \, +\infty)$ también tienen todas las propiedades estándar de las integrales definidas (con un correspondiente reformulación que tiene en cuenta el intervalo de integración de elección).
10.1.2 Criterios para la convergencia de integrales impropias de 1ª clase
Teorema (el primer signo de comparación). Sea $f(x)$, $g(x)$ continua para $x>a$, y sea $0 a$. Luego
1. Si la integral \[ \int _a^(+\infty)g(x)dx \] converge, entonces la integral \[ \int _a^(+\infty)f(x)dx también converge. \] 2. Si la integral \[ \int _a^(+\infty)f(x)dx \] diverge, entonces la integral \[ \int _a^(+\infty)g(x)dx también diverge. \]
Teorema (el segundo signo de comparación). Sean $f(x)$, $g(x)$ continuas y positivas para $x>a$, y sea un límite finito
\[ \theta = \lim_(x \rightarrow +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]
Entonces las integrales
\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]
convergen o divergen al mismo tiempo.
Considere la integral
\[ I=\int _1^(+\infty)\frac(1)(x+\sin x)\,dx. \]
El integrando es una función positiva en el intervalo de integración. Además, para $x \rightarrow +\infty$ tenemos:
$\sin x$ es una "pequeña" corrección del denominador. Más precisamente, si tomamos $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, entonces
\[ \lim _(x \rightarrow +\infty)\frac(f(x))(g(x))=\lim _(x \rightarrow +\infty)\frac(x)(x+\sin x) =1. \]
Aplicando el segundo criterio de comparación, llegamos a la conclusión de que nuestra integral converge o diverge simultáneamente con la integral
\[ \int _1^(+\infty)\frac(1)(x)\,dx . \]
Como se muestra en el ejemplo anterior, esta integral diverge ($k=1$). Por lo tanto, la integral original diverge.
Calcular la integral impropia o establecer su convergencia (divergencia).
1. \[ \int _(0)^(+\infty)e^(-ax)\,dx. \] 2. \[ \int _(0)^(+\infty)xe^(-x^2)\,dx. \] 3. \[ \int _(-\infty)^(+\infty)\frac(2xdx)(x^2+1). \] 4. \[ \int _(0)^(+\infty)\frac(xdx)((x+2)^3). \] 5. \[ \int _(-\infty)^(+\infty)\frac(dx)(x^2+2x+2). \] 6. \[ \int _(1)^(+\infty)\frac(lnx)(x^2)\,dx. \] 7. \[ \int _(1)^(+\infty)\frac(dx)((1+x)\sqrt(x)). \] 8. \[ \int _(0)^(+\infty)e^(-\sqrt(x))\,dx. \] 9. \[ \int _(0)^(+\infty)e^(-ax)\cos x\,dx. \] 10. \[ \int _(0)^(+\infty)\frac(xdx)(x^3+1). \]
Integral impropia con límite de integración infinito
A veces, una integral impropia de este tipo también se denomina integral impropia de primer tipo..gif" width="49" height="19 src=">.
Menos comunes son las integrales con un límite inferior infinito o con dos límites infinitos: .
Consideraremos el caso más popular https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? No, no siempre. integrandohttps://pandia.ru/text/80/057/images/image007_0.gif" ancho="47" alto="23 src=">
Representemos la gráfica del integrando en el dibujo. Un gráfico típico y un trapezoide curvilíneo para este caso se ve así:
integral impropiahttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", en otras palabras, el área también es infinita. Entonces puede ser. En este caso, decimos que la integral impropia diverge.
2) Pero. Por paradójico que parezca, el área de una figura infinita puede ser igual a… ¡un número finito! Por ejemplo: .. En el segundo caso, la integral impropia converge.
¿Qué sucede si debajo del eje se ubica un trapezoide curvilíneo infinito?.gif" width="217" height="51 src=">.
: 
.
Ejemplo 1
El integrando https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, lo que significa que todo está bien y la integral impropia se puede calcular usando el " método "regular".
Aplicación de nuestra fórmula https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">
Es decir, la integral impropia diverge y el área del trapezoide curvilíneo sombreado es igual a infinito.
¡Al resolver integrales impropias, es muy importante saber cómo se ven los gráficos de las principales funciones elementales!
Ejemplo 2
Calcular la integral impropia o establecer su divergencia.
Hagamos un dibujo: 
Primero, notamos lo siguiente: el integrando es continuo en el semiintervalo. Bien..gif" ancho="327" altura="53">
(1) Tomamos la integral más simple de una función de potencia (este caso especial se encuentra en muchas tablas). Es mejor mover inmediatamente el signo menos más allá del signo de límite para que no se interponga en los cálculos posteriores.
(2) Sustituimos los límites superior e inferior según la fórmula de Newton-Leibniz.
(3) Indicamos que https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Señores, esto se ha entendido durante mucho tiempo) y simplificar responder.
¡Aquí, el área de un trapezoide curvilíneo infinito es igual a un número finito! Increíble pero cierto.
Ejemplo 3
Calcular la integral impropia o establecer su divergencia.
El integrando es continuo en .
Primero, tratemos de encontrar la función antiderivada (integral indefinida).
¿A cuál de las integrales de tabla se parece el integrando? Me recuerda al arco tangente: 
. A partir de estas consideraciones, se sugiere que sería bueno obtener un cuadrado en el denominador. Esto se hace por sustitución.
Reemplacemos:
Siempre es útil realizar una comprobación, es decir, diferenciar el resultado obtenido:
Ahora encontramos la integral impropia:
(1) Escribimos la solución de acuerdo con la fórmula 
. Es mejor mover inmediatamente la constante más allá del signo del límite para que no interfiera en los cálculos posteriores.
(2) Sustituimos los límites superior e inferior de acuerdo con la fórmula de Newton-Leibniz..gif" width="56" height="19 src=">?
(3) Obtenemos la respuesta final. El hecho de que es útil saber de memoria.
Es posible que los estudiantes avanzados no encuentren la integral indefinida por separado y no usen el método de reemplazo, sino que usen el método de sumar la función bajo el signo diferencial y resuelvan la integral impropia "inmediatamente". En este caso, la solución debería ser algo como esto:
“
El integrando es continuo en https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“
Ejemplo 4
Calcular la integral impropia o establecer su divergencia.
! Este es un ejemplo típico, y las integrales similares son muy comunes. ¡Hazlo bien! La función antiderivada se encuentra aquí mediante el método de selección de cuadrados completos.
Ejemplo 5
Calcular la integral impropia o establecer su divergencia.
Esta integral se puede resolver en detalle, es decir, primero encuentra la integral indefinida cambiando la variable. Y puede resolverlo "inmediatamente", sumando la función bajo el signo del diferencial.
Integrales impropias de funciones ilimitadas
A veces, tales integrales impropias se denominan integrales impropias de segunda clase. Las integrales impropias del segundo tipo se "encriptan" astutamente bajo la integral definida habitual y se ven exactamente iguales: ..gif" width="39" height="15 src=">, 2) o en el punto, 3) o en ambos puntos a la vez, 4) o incluso en el intervalo de integración. Consideraremos los dos primeros casos, para los casos 3-4 al final del artículo hay un enlace a una lección adicional.
Solo un ejemplo para que quede claro: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, entonces nuestro denominador se vuelve cero, es decir, ¡el integrando simplemente no existe en este punto!
En general, al analizar la integral impropia siempre es necesario sustituir ambos límites de integración en el integrando..jpg" alt="(!LANG:Integral impropia, punto de discontinuidad en el límite inferior de integración" width="323" height="380">!}
Aquí casi todo es igual que en la integral de primera clase.
Nuestra integral es numéricamente igual al área del trapezoide curvilíneo sombreado, que no está acotado desde arriba. En este caso, puede haber dos opciones: la integral impropia diverge (el área es infinita) o la integral impropia es igual a un número finito (es decir, ¡el área de una figura infinita es finita!).
Solo queda modificar la fórmula de Newton-Leibniz. También se modifica con la ayuda del límite, pero el límite ya no tiende al infinito, sino valorarhttps://pandia.ru/text/80/057/images/image052.gif" ancho="28" alto="19"> a la derecha.
Ejemplo 6
Calcular la integral impropia o establecer su divergencia.
El integrando sufre una ruptura infinita en un punto (¡no olvides verificar verbalmente o en un borrador si todo está bien con el límite superior!)
Primero, calculamos la integral indefinida: 
Reemplazo: 
Calculamos la integral impropia:
(1) ¿Qué hay de nuevo aquí? Prácticamente nada en cuanto a técnica. Lo único que ha cambiado es la entrada bajo el icono de límite: . La adición significa que apuntamos al valor de la derecha (lo cual es lógico, vea el gráfico). Tal límite en la teoría de los límites se llama límite unilateral. En este caso, tenemos un límite por la derecha.
(2) Sustituimos los límites superior e inferior según la fórmula de Newton-Leibniz.
(3) Comprender https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. ¿Cómo determinar dónde debe ir la expresión? En términos generales, en solo tienes que sustituir el valor por ello, sustituir tres cuartos e indicar que... Peinamos la respuesta.
En este caso, la integral impropia es igual a un número negativo.
Ejemplo 7
Calcular la integral impropia o establecer su divergencia.
Ejemplo 8
Calcular la integral impropia o establecer su divergencia.
Si el integrando no existe en el punto
Un trapezoide curvilíneo infinito para tal integral impropia fundamentalmente se ve así:
Aquí todo es exactamente igual, excepto que el límite tiende a valorarhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> debemos acercarnos infinitamente al punto de ruptura izquierda.
Integrales impropias de primera clase: difusión del concepto integral definida para los casos de integrales con infinitos límites superior o inferior de integración, o ambos límites de integración son infinitos.
Integrales impropias de segunda especie: extensión del concepto de integral definida a los casos de integrales de funciones ilimitadas, el integrando no existe en un número finito de puntos del intervalo finito de integración, tendiendo al infinito.
Para comparacion. Al introducir el concepto de integral definida, se asumió que la función F(X) es continua en el segmento [ a, B], y el intervalo de integración es finito, es decir, está limitado por números, y no por infinito. Algunas tareas llevan a la necesidad de abandonar estas restricciones. Así es como aparecen las integrales impropias.
El significado geométrico de la integral impropia resulta ser bastante simple. Cuando la gráfica de la función y = F(X) está por encima del eje Buey, la integral definida expresa el área de un trapezoide curvilíneo delimitado por una curva y = F(X) , abscisas y ordenadas X = a , X = B. A su vez, la integral impropia expresa el área de un trapezoide curvilíneo ilimitado (infinito) encerrado entre las líneas y = F(X) (en la foto de abajo en rojo) X = a y el eje de abscisas.
Las integrales impropias se definen de manera similar para otros intervalos infinitos:
El área de un trapezoide curvilíneo infinito puede ser un número finito, en cuyo caso la integral impropia se llama convergente. El área también puede ser infinita, en cuyo caso la integral impropia se llama divergente.
Usar el límite de una integral en lugar de la propia integral impropia. Para calcular la integral impropia, necesitas usar el límite de la integral definida. Si este límite existe y es finito (no igual a infinito), entonces la integral impropia se llama convergente, de lo contrario es divergente. A qué tiende la variable bajo el signo de límite depende de si se trata de una integral impropia de primera o de segunda clase. Averigüémoslo ahora.
Integrales impropias del primer tipo - con límites infinitos y su convergencia
Integrales impropias con un límite superior infinito
Entonces, el registro de la integral impropia difiere de la integral definida habitual en que el límite superior de integración es infinito.
Definición. Una integral impropia con un límite superior infinito de integración de función continua F(X) Entre a antes de ∞ se llama el límite de la integral de esta función con el límite superior de integración B y el límite inferior de integración a siempre que el límite superior de integración crezca indefinidamente, es decir.
.
Si este límite existe y es igual a algún número, y no al infinito, entonces la integral impropia se llama convergente, y se toma como valor el número igual al límite. De lo contrario la integral impropia se llama divergente y no se le atribuye ningún valor.
Ejemplo 1. Calcular integral impropia(si converge).
Solución. Con base en la definición de la integral impropia, encontramos
Dado que el límite existe y es igual a 1, entonces el dado integral impropia converge y es igual a 1.
En el siguiente ejemplo, el integrando es casi el mismo que en el ejemplo 1, solo que el grado de x no es dos, sino la letra alfa, y la tarea es estudiar la integral impropia para la convergencia. Es decir, queda la pregunta por responder: ¿a qué valores de alfa converge esta integral impropia y a qué valores diverge?
Ejemplo 2. Investiga la convergencia de una integral impropia(el límite inferior de integración es mayor que cero).
Solución. Supongamos primero que , luego
En la expresión resultante, pasamos al límite en:
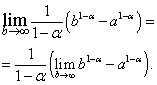
Es fácil ver que el límite en el lado derecho existe y cero, cuando , eso es , y no existe cuando , eso es .
En el primer caso, es decir, cuando . si, entonces 
y no existe.
La conclusión de nuestro estudio es la siguiente: integral impropia converge en y diverge en .
Aplicando la fórmula de Newton-Leibniz al tipo de integral impropia en estudio 
, podemos derivar la siguiente fórmula muy similar:
.
Esta es la fórmula generalizada de Newton-Leibniz.
Ejemplo 3. Calcular integral impropia(si converge).
El límite de esta integral existe:
La segunda integral, que es la suma que expresa la integral original:
El límite de esta integral también existe:
.
Encontramos la suma de dos integrales, que es también el valor de la integral impropia original con dos límites infinitos:
Integrales impropias de segundo tipo - de funciones ilimitadas y su convergencia
Deja que la función F(X) establecido en el segmento de a antes de B e ilimitado en él. Supongamos que la función tiende al infinito en el punto B , mientras que en todos los demás puntos del segmento es continuo.
Definición. Integral impropia de la función F(X) en el segmento de a antes de B se llama el límite de la integral de esta función con el límite superior de integración C , si al esforzarse C para B la función crece indefinidamente, y en el punto X = B función no definida, es decir.
.
Si existe este límite, entonces la integral impropia de la segunda especie se llama convergente, de lo contrario, divergente.
Usando la fórmula de Newton-Leibniz, derivamos.