Šajā rakstā mēs analizēsim tik svarīgu darbību ar decimāldaļskaitļiem kā dalīšana. Vispirms mēs formulējam visparīgie principi, tad mēs analizēsim, kā pareizi veikt sadalīšanu decimāldaļskaitļi kolonna gan citām daļām, gan naturāliem skaitļiem. Tālāk mēs analizēsim parasto daļskaitļu dalījumu decimāldaļās un otrādi, un beigās redzēsim, kā pareizi sadalīt daļas, kas beidzas ar 0, 1, 0, 01, 100, 10 utt.
Šeit mēs ņemam tikai gadījumus ar pozitīvām daļām. Ja pirms daļskaitļa ir mīnuss, tad, lai ar to rīkoties, ir jāizpēta materiāls par racionālo un reālo skaitļu dalījumu.
Yandex.RTB R-A-339285-1
Visas decimāldaļas, gan galīgas, gan periodiskas, ir tikai īpašs parasto daļskaitļu rakstīšanas veids. Tāpēc uz tiem attiecas tie paši principi, kas uz tiem atbilstošajām parastajām daļām. Tādējādi mēs reducējam visu decimālo daļu dalīšanas procesu līdz to aizstāšanai ar parastajām, kam seko aprēķins ar mums jau zināmām metodēm. Ņemsim konkrētu piemēru.
1. piemērs
Sadaliet 1,2 ar 0,48.
Risinājums
Mēs rakstām decimāldaļas parasto daļskaitļu veidā. Mēs varēsim:
1 , 2 = 12 10 = 6 5
0 , 48 = 48 100 = 12 25 .
Tādējādi mums ir jāsadala 6 5 ar 12 25. Mēs ticam:
1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2
No iegūtā nepareiza frakcija jūs varat izvēlēties visu daļu un iegūt jaukts numurs 2 1 2 vai arī varat to attēlot kā decimāldaļskaitli, lai tas atbilstu sākotnējiem skaitļiem: 5 2 \u003d 2, 5. Kā to izdarīt, mēs jau rakstījām iepriekš.
Atbilde: 1 , 2: 0 , 48 = 2 , 5 .
2. piemērs
Aprēķiniet, cik būs 0 , (504) 0 , 56 .
Risinājums
Pirmkārt, mums ir jāpārvērš periodiska decimāldaļdaļa par parasto.
0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111
Pēc tam mēs arī pārtulkosim pēdējo decimāldaļu citā formā: 0, 56 = 56 100. Tagad mums ir divi skaitļi, ar kuriem mums būs viegli veikt nepieciešamos aprēķinus:
0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111
Mums ir rezultāts, ko varam arī pārvērst decimāldaļās. Lai to izdarītu, sadaliet skaitītāju ar saucēju, izmantojot kolonnas metodi:
Atbilde: 0 , (504) : 0 , 56 = 0 , (900) .
Ja dalīšanas piemērā mēs satikām neperiodiskas decimāldaļas, tad mēs rīkosimies nedaudz savādāk. Mēs nevaram tos noapaļot līdz parastajām daļskaitļiem, tāpēc, dalot, vispirms tie ir jānoapaļo līdz noteiktam ciparam. Šī darbība ir jāveic gan ar dividendi, gan ar dalītāju: precizitātes labad noapaļosim arī esošo galīgo vai periodisko daļskaitli.
3. piemērs
Atrodiet, cik daudz būs 0, 779 ... / 1, 5602.
Risinājums
Vispirms abas daļdaļas noapaļo līdz simtdaļām. Lūk, kā mēs pārejam no bezgalīgām vienreizējām daļām uz ierobežotām decimāldaļām:
0 , 779 … ≈ 0 , 78
1 , 5602 ≈ 1 , 56
Varam turpināt aprēķinus un iegūt aptuvenu rezultātu: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78100: 156100 = 78100 100156 = 78156 = 12 = 0,5.
Rezultāta precizitāte būs atkarīga no noapaļošanas pakāpes.
Atbilde: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .
Kā dalīt naturālu skaitli ar decimāldaļu un otrādi
Dalīšanas pieeja šajā gadījumā ir gandrīz vienāda: ierobežotās un periodiskās daļas aizstājam ar parastajām, bet bezgalīgās neperiodiskās noapaļo. Sāksim ar dalīšanas piemēru ar naturālu skaitli un decimāldaļu.
4. piemērs
Sadaliet 2,5 ar 45.
Risinājums
Salīdzināsim 2, 5 parastas daļskaitļa formā: 255 10 \u003d 51 2. Tālāk mums tas vienkārši jāsadala dabiskais skaitlis. Mēs jau zinām, kā to izdarīt:
25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30
Ja rezultātu tulkojam decimāldaļās, tad iegūstam 0 , 5 (6) .
Atbilde: 25 , 5: 45 = 0 , 5 (6) .
Dalīšanas ar kolonnu metode ir laba ne tikai naturāliem skaitļiem. Pēc analoģijas mēs to varam izmantot arī frakcijām. Zemāk mēs norādīsim darbību secību, kas šim nolūkam jāveic.
1. definīcija
Lai decimāldaļskaitļu kolonnu dalītu ar naturāliem skaitļiem, jums ir:
1. Pievienojiet dažas nulles decimāldaļai labajā pusē (dalīšanai mēs varam pievienot jebkuru vajadzīgo skaitu).
2. Sadaliet decimāldaļu ar naturālu skaitli, izmantojot algoritmu. Kad daļdaļas veselās daļas dalījums beidzas, iegūtajā koeficientā ievietojam komatu un skaitam tālāk.
Šāda dalījuma rezultāts var būt vai nu galīga, vai bezgalīga periodiska decimāldaļdaļa. Tas ir atkarīgs no atlikuma: ja tas ir nulle, tad rezultāts būs ierobežots, un, ja atlikumi sāks atkārtot, tad atbilde būs periodiska daļa.
Kā piemēru ņemsim dažus uzdevumus un mēģināsim pabeigt šīs darbības ar konkrētiem skaitļiem.
5. piemērs
Aprēķiniet , cik būs 65 , 14 4 .
Risinājums
Mēs izmantojam kolonnu metodi. Lai to izdarītu, daļskaitlim pievienojiet divas nulles un iegūstiet decimāldaļu 65, 1400, kas būs vienāda ar oriģinālu. Tagad mēs rakstām kolonnu dalīšanai ar 4:

Iegūtais skaitlis būs vajadzīgās veselā skaitļa daļas dalīšanas rezultāts. Mēs ieliekam komatu, atdalot to, un turpinām:

Esam sasnieguši nulles atlikumu, tāpēc dalīšanas process ir pabeigts.
Atbilde: 65 , 14: 4 = 16 , 285 .
6. piemērs
Sadaliet 164,5 ar 27.
Risinājums
Vispirms sadalām daļējo daļu un iegūstam:
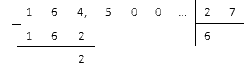
Iegūto skaitli atdalām ar komatu un turpinām dalīt:

Mēs redzam, ka atlikumi sāka periodiski atkārtot, un skaitļi deviņi, divi un pieci sāka mainīties koeficientā. Mēs apstāsimies pie tā un rakstīsim atbildi kā periodisku daļu 6, 0 (925) .
Atbilde: 164 , 5: 27 = 6 , 0 (925) .
Šādu dalījumu var reducēt uz privātās decimāldaļskaitļa un naturālā skaitļa atrašanas procesu, kas jau aprakstīts iepriekš. Lai to izdarītu, mums ir jāreizina dividende un dalītājs ar 10, 100 utt., lai dalītājs pārvērstos par naturālu skaitli. Pēc tam veicam iepriekš minēto darbību secību. Šī pieeja ir iespējama dalīšanas un reizināšanas īpašību dēļ. Burtiskā formā mēs tos rakstījām šādi:
a: b = (a 10) : (b 10) , a: b = (a 100) : (b 100) un tā tālāk.
Formulēsim noteikumu:
2. definīcija
Lai dalītu vienu pēdējo decimāldaļu ar citu, jums ir:
1. Dividendē un dalītājā pārvietojiet komatu pa labi pēc rakstzīmju skaita, kas nepieciešams, lai dalītāju pārvērstu par naturālu skaitli. Ja dividendē nav pietiekami daudz zīmju, mēs tai pievienojam nulles labajā pusē.
2. Pēc tam mēs dalām daļu ar kolonnu ar iegūto naturālo skaitli.
Apskatīsim konkrētu problēmu.
7. piemērs
Sadaliet 7 287 ar 2, 1.
Risinājums: Lai dalītāju padarītu par naturālu skaitli, mums ir jāpārvieto komats par vienu rakstzīmi pa labi. Tāpēc mēs pārgājām uz decimāldaļskaitļa 72, 87 dalīšanu ar 21. Iegūtos skaitļus ierakstīsim kolonnā un aprēķināsim

Atbilde: 7 , 287: 2 , 1 = 3 , 47
8. piemērs
Aprēķināt 16 , 3 0 , 021 .
Risinājums
Mums būs jāpārvieto komats līdz trīs cipariem. Šim nolūkam dalītājā nav pietiekami daudz ciparu, kas nozīmē, ka jums ir jāizmanto papildu nulles. Mēs domājam, ka gala rezultāts būs:

Mēs redzam 4., 19., 1., 10., 16., 13. atlikumu periodisku atkārtošanos. Koeficients atkārtojas 1 , 9 , 0 , 4 , 7 un 5 . Tad mūsu rezultāts ir periodiskā decimāldaļa 776 , (190476) .
Atbilde: 16 , 3: 0 , 021 = 776 , (190476)
Mūsu aprakstītā metode ļauj rīkoties pretēji, tas ir, naturālu skaitli dalīt ar pēdējo decimāldaļu. Apskatīsim, kā tas ir paveikts.
9. piemērs
Aprēķiniet, cik būs 3 5 , 4 .
Risinājums
Acīmredzot mums būs jāpārvieto komats pa labi par vienu rakstzīmi. Pēc tam mēs varam sākt dalīt 30, 0 ar 54. Ierakstīsim datus kolonnā un aprēķināsim rezultātu:
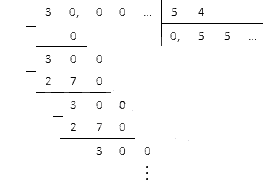
Atkārtojot atlikumu, mēs iegūstam skaitli 0 , (5) , kas ir periodiska decimāldaļa.
Atbilde: 3: 5 , 4 = 0 , (5) .
Kā dalīt decimāldaļas ar 1000, 100, 10 utt.
Saskaņā ar jau pētītajiem parasto daļskaitļu dalīšanas noteikumiem, daļdaļas dalīšana desmitos, simtos, tūkstošos ir līdzīga reizināšanai ar 1/1000, 1/100, 1/10 utt. Izrādās, ka, lai veiktu dalīšanu , šajā gadījumā pietiek tikai pārvietot komatu uz vēlamās summas cipariem. Ja pārsūtāmajā skaitā nav pietiekami daudz vērtību, jums jāpievieno nepieciešamais nulles skaits.
10. piemērs
Tātad, 56, 21: 10 = 5, 621 un 0, 32: 100 000 = 0, 0000032.
Bezgalīgu decimāldaļu gadījumā mēs rīkojamies tāpat.
11. piemērs
Piemēram, 3 , (56) : 1000 = 0 , 003 (56) un 593 , 374 ... : 100 = 5 , 93374 ... .
Kā dalīt decimāldaļas ar 0,001, 0,01, 0,1 utt.
Izmantojot to pašu noteikumu, mēs varam arī dalīt daļas ar norādītajām vērtībām. Šī darbība būs līdzīga reizināšanai ar attiecīgi 1000 , 100 , 10 . Lai to izdarītu, mēs pārvietojam komatu uz vienu, diviem vai trim cipariem atkarībā no problēmas apstākļiem un pievienojam nulles, ja ciparā nav pietiekami daudz ciparu.
12. piemērs
Piemēram, 5, 739: 0, 1 = 57, 39 un 0, 21: 0, 00001 = 21 000.
Šis noteikums attiecas arī uz bezgalīgām decimālzīmēm. Mēs tikai iesakām būt uzmanīgiem ar atbildē iegūtās daļas periodu.
Tātad, 7 , 5 (716) : 0 , 01 = 757 , (167) , jo pēc komata pārvietošanas decimāldaļā 7 , 5716716716 ... divi cipari pa labi, mēs saņēmām 757 , 167167 ... .
Ja piemērā mums ir neperiodiskas daļas, tad viss ir vienkāršāk: 394 , 38283 ... : 0 , 001 = 394382 , 83 ... .
Kā jauktu skaitli vai parasto daļskaitli dalīt ar decimāldaļu un otrādi
Mēs arī reducējam šo darbību uz darbībām ar parastajām daļām. Lai to izdarītu, jums ir jānomaina decimālskaitļi atbilstošās parastās daļskaitļus un ierakstiet jaukto skaitli kā nepareizu daļskaitli.
Ja dalām neperiodisku daļskaitli ar parastu vai jauktu skaitli, mums jārīkojas pretēji, aizstājot kopējā frakcija vai jaukts skaitlis ar atbilstošo decimāldaļu.
Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter
Noteikums decimāldaļu dalīšanai ar naturāliem skaitļiem.
Četras identiskas rotaļlietas kopā maksāja 921 rubli 20 kapeikas. Cik maksā viena rotaļlieta (skat. 1. att.)?
Rīsi. 1. Problēmas ilustrācija
Risinājums
Lai noskaidrotu vienas rotaļlietas izmaksas, šī summa jāsadala ar četriem. Pārrēķināsim summu kapeikās:

Atbilde: vienas rotaļlietas izmaksas ir 23 030 kapeikas, tas ir, 230 rubļi 30 kapeikas jeb 230,3 rubļi.
Šo problēmu var atrisināt, nepārvēršot rubļus kapeikās, tas ir, dalīt decimāldaļu ar naturālu skaitli:.
Lai dalītu decimāldaļdaļu ar naturālu skaitli, jums ir jādala daļa ar šo skaitli, jo naturālie skaitļi tiek dalīti, un jāievieto privātā komatā, kad veselā skaitļa daļas dalīšana ir beigusies.
Mēs sadalām kolonnā, kā dalām naturālos skaitļus. Pēc tam, kad esam nojaukuši skaitli 2 (desmito daļu skaits ir pirmais cipars aiz komata dividendes 921.20 ierakstā), koeficientā ievietojiet komatu un turpiniet dalīšanu:

Atbilde: 230,3 rubļi.
Mēs sadalām kolonnā, kā dalām naturālos skaitļus. Pēc tam, kad esam nojaukuši skaitli 6 (desmito daļu skaits ir skaitlis aiz komata dividendes ierakstā 437,6), koeficientā ievietojiet komatu un turpiniet dalīšanu:
Ja dividende ir mazāka par dalītāju, tad koeficients sāksies no nulles.
1 nedalās ar 19, tāpēc koeficientā ieliekam nulli. Veselās daļas dalīšana ir beigusies, privātajā ieliekam komatu. Nojaucam 7. 17 nedalās ar 19, privāti rakstām nulli. Mēs nojaucam 6 un turpinām sadalīšanu:

Mēs dalām, kā dalām naturālos skaitļus. Komatā mēs ieliekam komatu, tiklīdz noņemam 8 - pirmo ciparu pēc komata dividendē 74,8. Turpināsim dalīšanu. Atņemot, iegūstam 8, bet dalīšana nav beigusies. Mēs zinām, ka nulles var pievienot decimāldaļskaitļa beigās — tas nemainīs daļskaitļa vērtību. Mēs piešķiram nulli un sadalām 80 ar 10. Iegūstam 8 - dalīšana ir beigusies.

Lai decimāldaļu dalītu ar 10, 100, 1000 utt., šajā daļā esošais komats jāpārvieto par tik cipariem pa kreisi, cik dalītājā ir nulles aiz viena.

Šajā nodarbībā mēs uzzinājām, kā decimāldaļdaļu dalīt ar naturālu skaitli. Mēs izskatījām variantu ar parastu naturālu skaitli, kā arī variantu, kurā notiek dalīšana ar bitu vienību (10, 100, 1000 utt.).
Atrisiniet vienādojumus:
Atrast nezināms dalītājs, ir nepieciešams dalīt dividendi ar koeficientu. Tas ir .
Mēs sadalām kolonnā. Pēc tam, kad esam nojaukuši skaitli 4 (desmito daļu skaits ir pirmais cipars aiz komata dividendes 134.4 ierakstā), koeficientā ielieciet komatu un turpiniet dalīšanu:

Atrodiet koeficienta pirmo ciparu (dalīšanas rezultātu). Lai to izdarītu, sadaliet pirmo dividendes ciparu ar dalītāju. Ierakstiet rezultātu zem dalītāja.
- Mūsu piemērā dividendes pirmais cipars ir 3. Sadaliet 3 ar 12. Tā kā 3 ir mazāks par 12, tad dalīšanas rezultāts būs 0. Zem dalītāja ierakstiet 0 - tas ir koeficienta pirmais cipars.
Reiziniet rezultātu ar dalītāju. Ierakstiet reizināšanas rezultātu zem dividendes pirmā cipara, jo tas ir skaitlis, kuru tikko dalījāt ar dalītāju.
- Mūsu piemērā 0 × 12 = 0, tāpēc zem 3 ierakstiet 0.
Atņemiet reizināšanas rezultātu no dividendes pirmā cipara. Uzrakstiet savu atbildi jaunā rindā.
- Mūsu piemērā: 3 - 0 = 3. Ierakstiet 3 tieši zem 0.
Pārvietojiet uz leju dividendes otro ciparu. Lai to izdarītu, blakus atņemšanas rezultātam pierakstiet nākamo dividendes ciparu.
- Mūsu piemērā dividende ir 30. Dividendes otrais cipars ir 0. Pārvietojiet to uz leju, ierakstot 0 blakus 3 (atņemšanas rezultāts). Jūs saņemsiet numuru 30.
Sadaliet rezultātu ar dalītāju. Jūs atradīsit privātā numura otro ciparu. Lai to izdarītu, sadaliet skaitli apakšējā rindā ar dalītāju.
- Mūsu piemērā daliet 30 ar 12. 30 ÷ 12 = 2 plus daži atlikumi (jo 12 x 2 = 24). Aiz 0 zem dalītāja ierakstiet 2 - tas ir koeficienta otrais cipars.
- Ja nevarat atrast piemērotu ciparu, atkārtojiet ciparus, līdz jebkura cipara reizināšanas rezultāts ar dalītāju ir mazāks par skaitli, kas atrodas kolonnas pēdējā vietā, un ir vistuvāk tam. Mūsu piemērā apsveriet skaitli 3. Reiziniet to ar dalītāju: 12 x 3 = 36. Tā kā 36 ir lielāks par 30, skaitlis 3 nav piemērots. Tagad apsveriet skaitli 2. 12 x 2 = 24. 24 ir mazāks par 30, tāpēc skaitlis 2 ir pareizais risinājums.
Atkārtojiet iepriekš minētās darbības, lai atrastu nākamo ciparu. Aprakstītais algoritms tiek izmantots jebkurā garās dalīšanas uzdevumā.
- Otro koeficientu reiziniet ar dalītāju: 2 x 12 = 24.
- Ierakstiet reizināšanas rezultātu (24) zem pēdējā skaitļa kolonnā (30).
- Atņemiet mazāko skaitli no lielākā. Mūsu piemērā: 30 - 24 = 6. Ierakstiet rezultātu (6) jaunā rindā.
Ja dividendē ir atlikuši cipari, kurus var pārvietot uz leju, turpiniet aprēķina procesu. Pretējā gadījumā pārejiet pie nākamās darbības.
- Mūsu piemērā jūs pārvietojāt uz leju dividendes pēdējo ciparu (0). Tāpēc pārejiet pie nākamās darbības.
Ja nepieciešams, izmantojiet decimālzīmi, lai paplašinātu dividendi. Ja dividende vienmērīgi dalās ar dalītāju, tad pēdējā rindā jūs saņemsiet skaitli 0. Tas nozīmē, ka uzdevums ir atrisināts, un atbilde (vesela skaitļa formā) tiek ierakstīta zem dalītāja. Bet, ja kolonnas pašā apakšā ir kāds cits cipars, izņemot 0, jums ir jāpaplašina dividende, ievietojot komatu aiz komata un piešķirot 0. Atgādiniet, ka tas nemaina dividendes vērtību.
- Mūsu piemērā pēdējā rindā ir skaitlis 6. Tāpēc pa labi no 30 (dividende) ierakstiet decimālzīmi un pēc tam ierakstiet 0. Aiz komata ievietojiet arī pēc atrastajiem cipariem, kurus ierakstāt zem dalītājs (aiz šī komata vēl neko neraksti!) .
Atkārtojiet iepriekš minētās darbības, lai atrastu nākamo ciparu. Galvenais neaizmirst ielikt komatu gan pēc dividendes, gan pēc atrastajiem privātā cipariem. Pārējais process ir līdzīgs iepriekš aprakstītajam procesam.
- Mūsu piemērā pārvietojiet uz leju 0 (ko ierakstījāt aiz komata). Jūs saņemsiet skaitli 60. Tagad sadaliet šo skaitli ar dalītāju: 60 ÷ 12 = 5. Ierakstiet 5 aiz 2 (un aiz komata) zem dalītāja. Šis ir koeficienta trešais cipars. Tātad galīgā atbilde ir 2,5 (nulle 2 priekšā var ignorēt).
Pēdējā nodarbībā mēs iemācījāmies pievienot un atņemt decimāldaļskaitļus (skatiet nodarbību " Decimāldaļskaitļu pievienošana un atņemšana"). Tajā pašā laikā viņi novērtēja, cik daudz aprēķini ir vienkāršoti salīdzinājumā ar parastajām “divstāvu” daļām.
Diemžēl ar decimāldaļu reizināšanu un dalīšanu šis efekts nenotiek. Dažos gadījumos decimālzīme pat sarežģī šīs darbības.
Vispirms ieviesīsim jaunu definīciju. Mēs viņu satiksim diezgan bieži, un ne tikai šajā nodarbībā.
Nozīmīgākā skaitļa daļa ir viss starp pirmo un pēdējo ciparu, kas nav nulle, ieskaitot piekabes. Mēs runājam tikai par skaitļiem, komata zīme netiek ņemta vērā.
Iekļautie skaitļi nozīmīga daļa skaitļus sauc par zīmīgajiem cipariem. Tos var atkārtot un pat būt vienādi ar nulli.
Piemēram, apsveriet vairākas decimāldaļas un uzrakstiet tām atbilstošās nozīmīgās daļas:
- 91,25 → 9125 (nozīmīgi skaitļi: 9; 1; 2; 5);
- 0,008241 → 8241 (nozīmīgi skaitļi: 8; 2; 4; 1);
- 15,0075 → 150075 (nozīmīgi skaitļi: 1; 5; 0; 0; 7; 5);
- 0,0304 → 304 (nozīmīgi skaitļi: 3; 0; 4);
- 3000 → 3 (nozīmīgs skaitlis tikai viens: 3).
Lūdzu, ņemiet vērā: nulles skaitļa nozīmīgajā daļā nekur nepazūd. Mēs jau esam saskārušies ar kaut ko līdzīgu, kad iemācījāmies pārvērst decimāldaļdaļas parastajās (skatiet nodarbību “ Decimāldaļdaļas”).
Šis punkts ir tik svarīgs, un kļūdas šeit tiek pieļautas tik bieži, ka tuvākajā laikā publicēšu testu par šo tēmu. Noteikti trenējies! Un mēs, bruņojušies ar nozīmīgas daļas jēdzienu, faktiski turpināsim pie nodarbības tēmas.
Decimāldaļreizināšana
Reizināšanas operācija sastāv no trim secīgām darbībām:
- Katrai frakcijai pierakstiet nozīmīgāko daļu. Jūs saņemsiet divus parastus veselus skaitļus - bez saucējiem un decimālpunktiem;
- Reiziniet šos skaitļus ar jebkuru ērts veids. Tieši, ja skaitļi ir mazi, vai kolonnā. Mēs iegūstam ievērojamo daļu no vēlamās frakcijas;
- Uzziniet, kur un par cik cipariem ir nobīdīts decimālpunkts sākotnējās daļās, lai iegūtu atbilstošo nozīmīgo daļu. Veiciet atpakaļgaitas pārslēgšanu nozīmīgajai daļai, kas iegūta iepriekšējā darbībā.
Atgādināšu vēlreiz, ka nulles nozīmīgākās daļas malās nekad netiek ņemtas vērā. Šī noteikuma ignorēšana rada kļūdas.
- 0,28 12,5;
- 6,3 1,08;
- 132,5 0,0034;
- 0,0108 1600,5;
- 5,25 10 000.
Mēs strādājam ar pirmo izteiksmi: 0,28 12,5.
- Izrakstīsim skaitļu nozīmīgāko daļu no šīs izteiksmes: 28 un 125;
- Viņu produkts: 28 125 = 3500;
- Pirmajā reizinātājā decimālpunkts tiek pārvietots par 2 cipariem pa labi (0,28 → 28), bet otrajā - par vēl vienu ciparu. Kopumā ir nepieciešama nobīde pa kreisi par trim cipariem: 3500 → 3,500 = 3,5.
Tagad tiksim galā ar izteiksmi 6.3 1.08.
- Izrakstīsim zīmīgās daļas: 63. un 108.;
- Viņu produkts: 63 108 = 6804;
- Atkal divas nobīdes pa labi: attiecīgi par 2 un 1 cipariem. Kopā - atkal 3 cipari pa labi, tātad apgrieztā nobīde būs 3 cipari pa kreisi: 6804 → 6.804. Šoreiz beigās nav nulles.
Mēs nonācām pie trešās izteiksmes: 132,5 0,0034.
- Nozīmīgās daļas: 1325 un 34;
- Viņu produkts: 1325 34 = 45 050;
- Pirmajā daļā komata iet pa labi par 1 ciparu, bet otrajā - pat par 4. Kopā: 5 pa labi. Veicam nobīdi par 5 pa kreisi: 45050 → .45050 = 0.4505. Beigās tika noņemta nulle un pievienota priekšpusē, lai nepaliktu "pliks" komata zīme.
Šāda izteiksme: 0,0108 1600,5.
- Rakstām nozīmīgas daļas: 108 un 16 005;
- Mēs tos reizinām: 108 16 005 = 1 728 540;
- Skaitām skaitļus aiz komata: pirmajā ciparā ir 4, otrajā - 1. Kopā - atkal 5. Mums ir: 1 728 540 → 17,28540 = 17,2854. Beigās tika noņemta “papildu” nulle.
Visbeidzot, pēdējā izteiksme: 5,25 10 000.
- Nozīmīgās daļas: 525 un 1;
- Mēs tos reizinām: 525 1 = 525;
- Pirmā daļa tiek nobīdīta par 2 cipariem pa labi, bet otrā daļa tiek nobīdīta par 4 cipariem pa kreisi (10 000 → 1,0000 = 1). Kopā 4–2 = 2 cipari pa kreisi. Veicam apgriezto nobīdi par 2 cipariem pa labi: 525, → 52 500 (bija jāpievieno nulles).
pievērs uzmanību pēdējais piemērs: tā kā decimālzīme pārvietojas dažādos virzienos, kopējā nobīde notiek ar starpību. Tas ir ļoti svarīgs punkts! Šeit ir vēl viens piemērs:
Apsveriet skaitļus 1,5 un 12 500. Mums ir: 1,5 → 15 (pārbīdiet par 1 pa labi); 12 500 → 125 (2. maiņa pa kreisi). Mēs “pakāpjam” 1 ciparu pa labi un pēc tam 2 ciparus pa kreisi. Rezultātā mēs pakāpāmies par 2 − 1 = 1 ciparu pa kreisi.
Decimāldaļa
Sadalīšana, iespējams, ir visgrūtākā operācija. Protams, šeit jūs varat rīkoties pēc analoģijas ar reizināšanu: sadaliet nozīmīgās daļas un pēc tam “pārvietojiet” decimālzīmi. Bet šajā gadījumā ir daudz smalkumu, kas noliedz iespējamos ietaupījumus.
Tātad, aplūkosim vispārīgu algoritmu, kas ir nedaudz garāks, bet daudz uzticamāks:
- Pārvērst visas decimāldaļas parastajās daļskaitļos. Nedaudz praktizējot, šis solis prasīs dažu sekunžu jautājumu;
- Sadaliet iegūtās frakcijas klasiskais veids. Citiem vārdiem sakot, reiziniet pirmo daļu ar "apgriezto" otro (skatiet nodarbību " Skaitlisko daļu reizināšana un dalīšana");
- Ja iespējams, atgrieziet rezultātu kā decimāldaļu. Arī šis solis ir ātrs, jo bieži vien saucējam jau ir desmit pakāpē.
Uzdevums. Atrodiet izteiksmes vērtību:
- 3,51: 3,9;
- 1,47: 2,1;
- 6,4: 25,6:
- 0,0425: 2,5;
- 0,25: 0,002.
Mēs apsveram pirmo izteiksmi. Vispirms pārveidosim obi daļas decimāldaļās:
Mēs darām to pašu ar otro izteiksmi. Pirmās daļas skaitītājs atkal tiek sadalīts faktoros:

Trešajā un ceturtajā piemērā ir svarīgs punkts: pēc tam, kad tiek atbrīvots no decimāldaļas, parādās atceļamas daļas. Taču mēs šo samazinājumu neveiks.

Pēdējais piemērs ir interesants, jo otrās daļas skaitītājs ir pirmskaitlis. Šeit vienkārši nav ko faktorizēt, tāpēc mēs to uzskatām par “tukšu”:

Dažreiz dalīšanas rezultātā tiek iegūts vesels skaitlis (es runāju par pēdējo piemēru). Šajā gadījumā trešais solis netiek veikts vispār.
Turklāt dalot bieži parādās “neglītas” daļas, kuras nevar pārvērst decimāldaļās. Šeit dalīšana atšķiras no reizināšanas, kur rezultāti vienmēr tiek izteikti decimāldaļā. Protams, šajā gadījumā pēdējais solis atkal netiek veikts.
Pievērsiet uzmanību arī 3. un 4. piemēram. Tajos mēs apzināti nesamazinām parastās frakcijas atvasināts no decimāldaļām. Pretējā gadījumā tas sarežģīs apgriezto problēmu - galīgās atbildes attēlošanu decimāldaļā.
Atcerieties: daļskaitļa pamatīpašība (tāpat kā jebkura cita matemātikas likuma) pati par sevi nenozīmē, ka tā ir jāpiemēro visur un vienmēr, pie katras iespējas.
Dalīšana ar decimāldaļu ir tāda pati kā dalīšana ar naturālu skaitli.
Noteikums skaitļa dalīšanai ar decimāldaļu
Lai dalītu skaitli ar decimāldaļskaitli, gan dividendē, gan dalītājā jāpārvieto komats pa labi tik daudz ciparu, cik ir dalītājam aiz komata. Pēc tam dala ar naturālu skaitli.
Piemēri.
Veiciet dalīšanu ar decimāldaļu:
Lai dalītu ar decimāldaļu, komats jāpārvieto pa labi gan dividendē, gan dalītājā, cik dalītājā ir aiz komata, tas ir, ar vienu zīmi. Mēs iegūstam: 35,1: 1,8 \u003d 351: 18. Tagad mēs veicam sadalīšanu ar stūri. Rezultātā mēs iegūstam: 35,1: 1,8 = 19,5.
 2) 14,76: 3,6
2) 14,76: 3,6
Lai veiktu decimāldaļskaitļu dalīšanu gan dividendēs, gan dalītājā, pārvietojiet komatu pa labi par vienu zīmi: 14,76: 3,6 \u003d 147,6: 36. Tagad mēs veicam naturālu skaitli. Rezultāts: 14,76: 3,6 = 4,1.
Lai veiktu dalīšanu ar naturāla skaitļa decimāldaļu, gan dividendē, gan dalītājā ir jāpārvieto pa labi tik daudz rakstzīmju, cik ir dalītājam aiz komata. Tā kā šajā gadījumā dalītājā komats netiek ierakstīts, trūkstošo rakstzīmju skaitu aizpildām ar nullēm: 70: 1,75 \u003d 7000: 175. Iegūtos naturālos skaitļus sadalām ar stūri: 70: 1,75 \u003d 7000: 175 \u003d 40.
4) 0,1218: 0,058
Lai dalītu vienu decimāldaļskaitli citā, komatu pa labi gan dividendē, gan dalītājā pārvietojam par tik cipariem, cik ir dalītājā aiz komata, tas ir, ar trim cipariem. Tādējādi 0,1218: 0,058 \u003d 121,8: 58. Dalīšana ar decimāldaļu tika aizstāta ar dalīšanu ar naturālu skaitli. Mums ir viens stūris. Mums ir: 0,1218: 0,058 = 121,8: 58 = 2,1.
 5) 0,0456: 3,8
5) 0,0456: 3,8
