Nga përkufizimi rezulton se mund të flasim për vazhdimësi vetëm në lidhje me ato pika në të cilat përcaktohet f (x) (kur caktohet kufiri i një funksioni, një kusht i tillë nuk ishte vendosur). Për funksione të vazhdueshme
, pra, operacionet f dhe lim commute. Sipas dy përkufizimeve të kufirit të një funksioni në një pikë, mund të jepen dy përkufizime të vazhdimësisë - "në gjuhën e sekuencave" dhe "në gjuhën e pabarazive" (në gjuhën e ε-δ). Rekomandohet ta bëni vetë. Për përdorim praktik ndonjëherë është më e përshtatshme për të përcaktuar vazhdimësinë në gjuhën e rritjeve.
Vlera Δx = x-x 0 quhet rritje e argumentit, dhe Δy = f (x) -f (x 0) - rritja e funksionit kur kalon nga pika x 0 në pikën x.
Përkufizimi. Le të përcaktohet f (x) në pikën x 0. Një funksion f (x) quhet i vazhdueshëm në një pikë x 0 nëse një rritje infinite vogël e argumentit në këtë pikë korrespondon me një rritje infiniteminale të funksionit, domethënë Δy → 0 si Δx → 0.
Shembulli 1.
Vërtetoni se funksioni y = sinx është i vazhdueshëm për çdo vlerë të x.
Zgjidhje.
Le të jetë x 0 një pikë arbitrare. Duke i dhënë një rritje Δx, marrim pikën x = x 0 + Δx. Pastaj 
... marrim 
.
Përkufizimi.
Funksioni y = f (x) quhet i vazhdueshëm në pikën x 0 në të djathtë (majtas) nëse
.
Një funksion që është i vazhdueshëm në një pikë të brendshme do të jetë njëkohësisht i vazhdueshëm në të djathtë dhe në të majtë. E kundërta është gjithashtu e vërtetë: nëse një funksion është i vazhdueshëm në një pikë majtas dhe djathtas, atëherë ai do të jetë i vazhdueshëm në këtë pikë. Sidoqoftë, funksioni mund të jetë i vazhdueshëm vetëm në njërën anë. Për shembull, për 
, 
, f (1) = 1, prandaj, ky funksion është i vazhdueshëm vetëm në të majtë (shih grafikun e këtij funksioni në seksionin 5.7.2 më lart).
Përkufizimi.
Një funksion quhet i vazhdueshëm në një interval nëse është i vazhdueshëm në çdo pikë të këtij intervali.
Në veçanti, nëse intervali është një segment, atëherë në skajet e tij supozohet vazhdimësia e njëanshme.
Vetitë e funksioneve të vazhdueshme
1. Të gjitha funksionet elementare janë të vazhdueshme në fushën e tyre të përkufizimit.2. Nëse f (x) dhe φ (x), të dhëna në një interval, janë të vazhdueshme në pikën x 0 të këtij intervali, atëherë edhe funksionet do të jenë të vazhdueshme në këtë pikë.
3. Nëse y = f (x) është i vazhdueshëm në një pikë x 0 nga X, dhe z = φ (y) është i vazhdueshëm në pikën përkatëse y 0 = f (x 0) nga Y, atëherë funksioni kompleks z = φ (f (x )) do të jetë i vazhdueshëm në pikën x 0.
Ndërprerjet e funksioneve dhe klasifikimi i tyre
Shenja e vazhdimësisë së funksionit f (x) në pikën x 0 është barazi, që nënkupton praninë e tre kushteve:1) f (x) është përcaktuar në pikën x 0;
2)
;
3) .
Nëse të paktën një nga këto kërkesa shkelet, atëherë x 0 quhet pikë e ndërprerjes së funksionit. Me fjalë të tjera, pika e ndërprerjes është pika në të cilën ky funksion nuk është i vazhdueshëm. Nga përkufizimi i pikave të ndërprerjes del se pikat e ndërprerjes së funksionit janë:
a) pikat që i përkasin domenit të funksionit, në të cilat f (x) humbet vetinë e vazhdimësisë,
b) pikat që nuk i përkasin domenit të përkufizimit f (x), të cilat janë pika ngjitur të dy intervaleve të fushës së përcaktimit të funksionit.
Për shembull, për një funksion, pika x = 0 është një pikë ndërprerjeje, pasi funksioni në këtë pikë nuk është i përcaktuar, dhe funksioni
ka një ndërprerje në pikën x = 1, e cila është ngjitur për dy intervale (-∞, 1) dhe (1, ∞) të domenit f (x) dhe nuk ekziston. Për pikat e ndërprerjes, është miratuar klasifikimi i mëposhtëm.
1) Nëse në pikën x 0 ka të fundme 
dhe 
, por f (x 0 +0) ≠ f (x 0 -0), atëherë x 0 quhet pika e thyerjes së llojit të parë
, në të njëjtën kohë ata thërrasin funksioni i kërcimit
.
Shembulli 2.
Merrni parasysh funksionin 
Funksioni mund të jetë i ndërprerë vetëm në pikën x = 2 (në pikat e tjera është i vazhdueshëm si çdo polinom). 
Gjej 
, 
... Meqenëse kufijtë e njëanshëm janë të fundëm, por jo të barabartë me njëri-tjetrin, në pikën x = 2 funksioni ka një ndërprerje të llojit të parë. vini re, se 
, pra funksioni në këtë pikë është i vazhdueshëm në të djathtë (Fig. 2).
2) Pikat e thyerjes së llojit të dytë
janë pikat në të cilat të paktën njëri nga kufijtë e njëanshëm është i barabartë me ∞ ose nuk ekziston.
Shembulli 3.
Funksioni y = 2 1 / x është i vazhdueshëm për të gjitha vlerat e x përveç x = 0. Le të gjejmë kufijtë e njëanshëm: 
, 
, pra x = 0 është një pikë ndërprerjeje e llojit të dytë (Fig. 3).
3) Quhet pika x = x 0 pika e ndërprerjes së lëvizshme
nëse f (x 0 +0) = f (x 0 -0) ≠ f (x 0).
Hendeku "eliminohet" në kuptimin që mjafton të ndryshohet (ripërcaktohet ose ripërcaktohet) vlera e funksionit në këtë pikë, vendosje dhe funksioni bëhet i vazhdueshëm në pikën x 0. 
Shembulli 4.
Dihet se 
, dhe ky kufi nuk varet nga mënyra se si x tenton në zero. Por funksioni në pikën x = 0 është i papërcaktuar. Nëse zgjerojmë përkufizimin e një funksioni duke vendosur f (0) = 1, atëherë ai rezulton të jetë i vazhdueshëm në këtë pikë (në pika të tjera është i vazhdueshëm si një herës i vazhdueshëm funksionet sinx dhe x). 
Shembulli 5.
Hulumtoni vazhdimësinë e një funksioni 
.
Zgjidhje.
Funksionet y = x 3 dhe y = 2x janë të përcaktuara dhe të vazhdueshme kudo, përfshirë në intervalet e treguara. Ne hetojmë pikën e kryqëzimit të intervaleve x = 0: 
, 
,. Marrim atë, prej nga rezulton se në pikën x = 0 funksioni është i vazhdueshëm.
Përkufizimi.
Një funksion që është i vazhdueshëm në një interval me përjashtim të një numri të kufizuar pikash ndërprerje të llojit të parë ose ndërprerje të lëvizshme quhet pjesë-pjesë i vazhdueshëm në këtë interval.
Shembuj të funksioneve të ndërprera
Shembulli 1.
Funksioni është i përcaktuar dhe i vazhdueshëm në (-∞, + ∞) me përjashtim të pikës x = 2. Le të përcaktojmë llojin e pushimit. Për aq sa 
dhe 
, atëherë në pikën x = 2 ka një ndërprerje të llojit të dytë (Fig. 6). 
Shembulli 2.
Funksioni është i përcaktuar dhe i vazhdueshëm për të gjitha x përveç x = 0, ku emëruesi është zero... Gjeni kufijtë e njëanshëm në pikën x = 0: Kufijtë e njëanshëm janë të fundëm dhe të ndryshëm, prandaj, x = 0 është një pikë ndërprerjeje e llojit të parë (Fig. 7).
Shembulli 3.
Përcaktoni në cilat pika dhe çfarë lloj ndërprerjesh ka funksioni 
Ky funksion është përcaktuar në [-2,2]. Meqenëse x 2 dhe 1 / x janë të vazhdueshme, përkatësisht, në intervalet [-2,0] dhe, hendeku mund të jetë vetëm në kryqëzimin e intervaleve, domethënë në pikën x = 0. Meqenëse, atëherë x = 0 është një pikë ndërprerjeje e llojit të dytë.
Shembulli 4.
A është e mundur të mbyllni boshllëqet e funksionit:
a) në pikën x = 2;
b) 
në pikën x = 2;
v) 
në pikën x = 1?
Zgjidhje.
Rreth shembullit a), mund të themi menjëherë se ndërprerja f (x) në pikën x = 2 nuk mund të eliminohet, pasi në këtë pikë ka kufij të pafund të njëanshëm (shih shembullin 1).
b) Funksioni g (x), megjithëse ka kufij të fundëm të njëanshëm në pikën x = 2
(
,
),
por ato nuk përkojnë, kështu që as hendeku nuk mund të mbyllet.
c) Funksioni φ (x) në pikën e ndërprerjes x = 1 ka kufij të fundëm të barabartë të njëanshëm:. Prandaj, hendeku mund të eliminohet duke ripërcaktuar funksionin në pikën x = 1, nëse vendosim f (1) = 1 në vend të f (1) = 2.
Shembulli 5. Tregoni se funksioni Dirichlet
është i ndërprerë në çdo pikë të boshtit numerik.
Zgjidhje. Le të jetë x 0 çdo pikë nga (-∞, + ∞). Në cilindo nga rrethinat e tij, ka pika racionale dhe irracionale. Kjo do të thotë se në çdo lagje të x 0 funksioni do të ketë vlera të barabarta me 0 dhe 1. Në këtë rast, kufiri i funksionit në pikën x 0 nuk mund të ekzistojë as në të majtë as në të djathtë, kështu që Dirichlet funksioni ka ndërprerje të llojit të dytë në secilën pikë të boshtit numerik.
Shembulli 6. Gjeni pikat e ndërprerjes së një funksioni
dhe përcaktoni llojin e tyre.
Zgjidhje. Pikat e dyshimta për një boshllëk janë pikat x 1 = 2, x 2 = 5, x 3 = 3.
Në pikën x 1 = 2 f (x) ka një ndërprerje të llojit të dytë, pasi
.
Pika x 2 = 5 është një pikë vazhdimësie, pasi vlera e funksionit në këtë pikë dhe në afërsi të tij përcaktohet nga rreshti i dytë, jo nga i pari:.
Shqyrtoni pikën x 3 = 3:,
, prej nga rrjedh se x = 3 është një pikë ndërprerjeje e llojit të parë. Për një zgjidhje të pavarur.
Ekzaminoni funksionet për vazhdimësinë dhe përcaktoni llojin e pikave të ndërprerjes:
1) 
; Përgjigje: x = -1 - pika e ndërprerjes së lëvizshme;
2) 
; Përgjigje: Pushim i llojit të dytë në pikën x = 8;
3) 
; Përgjigje: Mosvazhdimësi e llojit të parë në x = 1;
4) 
Përgjigje: Në pikën x 1 = -5 ka një hendek të heqshëm, në x 2 = 1 - një hendek i llojit të dytë, dhe në pikën x 3 = 0 - një hendek i llojit të parë.
5) Si duhet zgjedhur numri A që funksioni 
do të ishte e vazhdueshme në pikën x = 0?
Përgjigje: A = 2.
6) A është e mundur të zgjedhësh numrin A në mënyrë që funksioni 
do të ishte e vazhdueshme në x = 2?
Përgjigja është jo.
Vazhdimësia e funksionit në interval
| Emri i parametrit | Kuptimi |
| Tema e artikullit: | Vazhdimësia e funksionit në interval |
| Kategoria (kategoria tematike) | Matematika |
Përkufizimi. Një funksion zakonisht quhet i vazhdueshëm në një interval nëse është i vazhdueshëm në secilën pikë të këtij intervali.
Nëse funksioni është përcaktuar në X=a dhe ku f(X) = f(a),
atëherë ata thonë se f(X) në pikën dhe është e vazhdueshme në të djathtë... Në mënyrë të ngjashme, nëse f(X) = f(b), atëherë ata thonë se në pikë b këtë funksion e vazhdueshme majtas.
Përkufizimi. Funksioni zakonisht quhet i vazhdueshëm në segmentin [ a, b], nëse është i vazhdueshëm në secilën pikë (në pikë aështë e vazhdueshme në të djathtë, në pikë b- e vazhdueshme në të majtë).
Vlera më e lartë funksione në = f(x) në segmentin [ a, b f(x 1) atë f(x) £ f(x 1) për të gjithë X Î [ a, b].
Vlera më e vogël funksione në = f(x) në segmentin [ a, b] është zakon të quhet kuptimi i saj f(x 2) atë f(x) ³ f(x 2) për të gjithë X Î [ a, b].
Funksionet që janë të vazhdueshme në një segment kanë një sërë vetish të rëndësishme, të cilat shprehen me teoremat e mëposhtme.
Teorema 3.3.1. Një funksion që është i vazhdueshëm në segmentin [ a, b], arrin vlerën më të ulët mbi të m dhe vlera më e madhe M, domethënë ka pika të tilla x 1 dhe x 2 të këtij segmenti që f(x 1) = m, f(x 2) = M.
Teorema ka një kuptim të thjeshtë gjeometrik (shih Fig. 2).
 |
Teorema 3.3.2. Nëse funksioni në = f(x) është e vazhdueshme në segmentin [ a, b] dhe merr vlera të pabarabarta në skajet e saj f(a) = A, f(b) = B, A ¹ B, atëherë cilido qoftë numri C midis A dhe B, ka një pikë Me Î [ a, b] sikurse f(Me) = C.
Kuptimi gjeometrik i teoremës është ilustruar në figurën 3. Çdo të drejtë në= С, ku A< C < B (или A >C> B), kryqëzon grafikun e funksionit në = f(x).
Pasoja. Nëse funksioni është i vazhdueshëm në një segment dhe merr vlera të shenjave të ndryshme në skajet e tij, atëherë në këtë segment ka të paktën një pikë në të cilën funksioni zhduket.
Kuptimi gjeometrik i përfundimit është ilustruar në Fig. 4.
Pyetje për vetëkontroll
1. Cili funksion quhet zakonisht i vazhdueshëm në një pikë?
2. Jepni një përkufizim tjetër ekuivalent për sa i përket rritjes së funksionit dhe argumenteve.
3. Çfarë mund të thoni për shumën, ndryshimin, produktin dhe herësin e dy funksioneve të vazhdueshme?
4. Për cilat vlera të argumentit të gjithë funksionet racionale racionale dhe thyesore janë të vazhdueshme?
5. Kur funksioni kompleks është i vazhdueshëm në një pikë?
6. Çfarë quhet zakonisht pika e ndërprerjes së funksioneve?
7. Cilat pika quhen pika të thyerjes së llojit të parë?
8. Cila sasi quhet zakonisht kërcim i funksionit?
9. Shpjegoni konceptet e "" pikës së një thyerjeje të lëvizshme "". Jep shembuj.
10. Cilat pika quhen pika të thyerjes së llojit të dytë? Jep shembuj.
11. Shpjegoni konceptet: "" vazhdimësi në intervalin "", "" vazhdimësi në të djathtë "", "" vazhdimësi në të majtë "", "" vazhdimësi në segmentin "".
12. Jepni përkufizimin e vlerave më të larta dhe më të ulëta të funksioneve.
13. Formuloni një teoremë për lidhjen e vazhdimësisë në segmentin me vlerat më të mëdha dhe më të vogla të funksionit. Shpjegojeni në foto.
14. Formuloni një teoremë për lidhjen midis vazhdimësisë së funksioneve në një interval dhe një intervali të vlerave të funksioneve. Ilustroni kuptimin e tij gjeometrik në figurë.
15. Jepni një përfundim për teoremën e mësipërme dhe interpretimin gjeometrik të saj.
LEKTURA Nr.4
Tema e ligjëratës: Derivat i një funksioni
Plani i leksionit: Koncepti i një derivati, kuptimi i tij gjeometrik dhe fizik. Rregullat themelore të diferencimit. Derivat funksion kompleks... Disa aplikacione derivative.
4.1. Koncepti i një derivati, kuptimi i tij gjeometrik dhe fizik
Merrni parasysh funksionin në = f(x) e specifikuar në intervalin] a, b[. Le XÎ ] a, b[dhe X Î ] a, b[, pastaj rritja e funksionit në pikë X 0 shprehet me formulën D në = f(x 0 + D X) – f(x 0).
Përkufizimi. Derivati i funksionit y = f(x) në pikën X 0 është zakon të quhet kufiri i raportit të rritjes së këtij funksioni me rritjen e argumentit kur ky i fundit tenton në zero:
f'(x 0) = 
ose y"(x 0) =.
Kuptimi gjeometrik i derivatit: derivati i këtij funksioni në një pikë është i barabartë me tangjenten e këndit ndërmjet boshtit Ox dhe tangjentes me grafikun e këtij funksioni në pikën përkatëse (shih Fig. 1):
f"(x 0) = tg a.
Në këtë mësim, ne do të mësojmë të vendosim vazhdimësinë e një funksioni. Ne do ta bëjmë këtë me ndihmën e kufijve, dhe të njëanshëm - djathtas dhe majtas, të cilat nuk janë aspak të frikshme, pavarësisht se ato janë shkruar si dhe.
Por cila është vazhdimësia e një funksioni në përgjithësi? Derisa të arrijmë në një përkufizim të rreptë, është më e lehtë të imagjinojmë një vijë që mund të vizatohet pa hequr lapsin nga letra. Nëse vizatohet një vijë e tillë, atëherë ajo është e vazhdueshme. Kjo linjë është grafiku i një funksioni të vazhdueshëm.
Grafikisht, një funksion është i vazhdueshëm në një pikë nëse grafiku i tij nuk "prihet" në atë pikë. Grafiku i një funksioni të tillë të vazhdueshëm - 
treguar në figurën e mëposhtme.
Përcaktimi i vazhdimësisë së një funksioni përmes kufirit. Një funksion është i vazhdueshëm në një pikë nëse plotësohen tre kushte:
1. Funksioni përcaktohet në një pikë.
Nëse të paktën një nga kushtet e listuara nuk plotësohet, funksioni nuk është i vazhdueshëm në pikë. Në këtë rast, ata thonë se funksioni ka një ndërprerje, dhe pikat në grafik në të cilat grafiku ndërpritet quhen pika të ndërprerjes së funksionit. Grafiku i një funksioni të tillë, i cili është i ndërprerë në pikën x = 2, është paraqitur në figurën më poshtë.
Shembulli 1. Funksioni f(x) përcaktohet si më poshtë:
A do të jetë ky funksion i vazhdueshëm në secilën nga pikat kufitare të degëve të tij, pra në pikat x = 0 , x = 1 , x = 3 ?
Zgjidhje. Kontrollojmë të tre kushtet për vazhdimësinë e funksionit në çdo pikë kufitare. Kushti i parë plotësohet, që nga fakti se funksioni i përcaktuar në secilën nga pikat kufitare rrjedh nga përkufizimi i funksionit. Mbetet për të kontrolluar dy kushtet e tjera.
Pika x= 0. Gjeni kufirin e majtë në këtë pikë:
.
Le të gjejmë kufirin e djathtë:
x Duhet të gjendet = 0 për degën e funksionit që përfshin këtë pikë, pra degën e dytë. Ne i gjejmë ato:
Siç mund ta shihni, kufiri i funksionit dhe vlera e funksionit në pikë x= 0 janë të barabarta. Prandaj, funksioni është i vazhdueshëm në pikë x = 0 .
Pika x= 1. Gjeni kufirin e majtë në këtë pikë:
Le të gjejmë kufirin e djathtë:
Kufiri i funksionit dhe vlera e funksionit në pikë x Duhet gjetur = 1 për atë degë të funksionit që përfshin këtë pikë, pra degën e dytë. Ne i gjejmë ato:
.
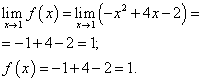Kufiri i funksionit dhe vlera e funksionit në pikë x= 1 janë të barabarta. Prandaj, funksioni është i vazhdueshëm në pikë x = 1 .
Pika x= 3. Gjeni kufirin e majtë në këtë pikë:
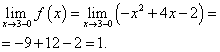
Le të gjejmë kufirin e djathtë:
Kufiri i funksionit dhe vlera e funksionit në pikë x= 3 duhet gjetur për atë degë të funksionit që përfshin këtë pikë, pra degën e dytë. Ne i gjejmë ato:
.
Kufiri i funksionit dhe vlera e funksionit në pikë x= 3 janë të barabarta. Prandaj, funksioni është i vazhdueshëm në pikë x = 3 .
Përfundimi kryesor: ky funksion është i vazhdueshëm në çdo pikë kufitare.
Vendosni vetë vazhdimësinë e funksionit në një pikë dhe më pas shikoni zgjidhjen
Ndryshimi i vazhdueshëm në një funksion mund të përkufizohet si një ndryshim gradual pa kërcime, në të cilin një ndryshim i vogël në argument sjell një ndryshim të vogël në funksion.
Le ta ilustrojmë këtë ndryshim të vazhdueshëm të funksionit me një shembull.
Lëreni një ngarkesë të varet mbi tryezë. Nën veprimin e kësaj ngarkese, filli shtrihet, pra distanca l pesha nga pika e pezullimit të fillit është një funksion i peshës së peshës m, kjo eshte l = f(m) , m≥0 .
Nëse e ndryshojmë pak masën e ngarkesës, atëherë distancën l ndryshim i vogël: ndryshime të vogla m korrespondojnë ndryshimet e vogla l... Megjithatë, nëse masa e ngarkesës është afër rezistencës në tërheqje të fillit, atëherë një rritje e lehtë në peshën e ngarkesës mund të shkaktojë thyerjen e fillit: distancë l do të rritet papritur dhe do të bëhet e barabartë me distancën nga pika e pezullimit në sipërfaqen e tryezës. Grafiku i funksionit l = f(m) treguar në figurë. Në vend, ky grafik është një vijë e vazhdueshme (e ngurtë) dhe në një pikë është e ndërprerë. Rezultati është një grafik me dy degë. Në të gjitha pikat përveç funksionit l = f(m) është i vazhdueshëm dhe në pikën ka një ndërprerje.
Studimi i një funksioni për vazhdimësi mund të jetë njëkohësisht një detyrë e pavarur dhe një nga fazat e një studimi të plotë të një funksioni dhe ndërtimi i grafikut të tij.
Vazhdimësia e funksionit në interval
Lëreni funksionin y = f(x) përcaktuar në interval] a, b[dhe është i vazhdueshëm në çdo pikë të këtij intervali. Atëherë quhet e vazhdueshme në interval] a, b[. Koncepti i vazhdimësisë së një funksioni në intervale të formës] - ∞, b[ , ]a, + ∞ [,] - ∞, + ∞ [. Tani lëreni funksionin y = f(x) është përcaktuar në segmentin [ a, b]. Dallimi midis intervalit dhe linjës: Pikat fundore të intervalit nuk përfshihen në interval, dhe pikat fundore të linjës përfshihen në rresht. Këtu duhet përmendur të ashtuquajturën vazhdimësi të njëanshme: në pikë a, duke mbetur në segmentin [ a, b], ne mund të afrohemi vetëm nga e djathta dhe deri në pikën b- vetëm në të majtë. Funksioni quhet i vazhdueshëm në segmentin [ a, b], nëse është i vazhdueshëm në të gjitha pikat e brendshme të këtij segmenti, është i vazhdueshëm në të djathtë në pikë a dhe është i vazhdueshëm në të majtë në pikë b.
Secili prej funksioneve elementare mund të shërbejë si shembull i një funksioni të vazhdueshëm. Çdo funksion elementar është i vazhdueshëm në çdo segment në të cilin është përcaktuar. Për shembull, funksionet dhe janë të vazhdueshme në çdo segment [ a, b], funksioni është i vazhdueshëm në segmentin [ 0 , b], funksioni është i vazhdueshëm në çdo segment që nuk përmban pikën a = 2 .
Shembulli 4. Shqyrtoni funksionin për vazhdimësi.
Zgjidhje. Ne kontrollojmë kushtin e parë. Funksioni nuk është i përcaktuar në pikat - 3 dhe 3. Të paktën një nga kushtet për vazhdimësinë e funksionit në të gjithë vijën numerike nuk plotësohet. Prandaj, ky funksion është i vazhdueshëm në intervale
.Shembulli 5. Përcaktoni në cilën vlerë të parametrit a të vazhdueshme gjatë gjithë kohës fushat e përkufizimit funksionin 
Zgjidhje.
Le të gjejmë kufirin e djathtë në:
.
Natyrisht, vlera në pikë x= 2 duhet të jetë e barabartë sëpatë :
a = 1,5 .
Shembulli 6. Përcaktoni në cilat vlera të parametrave a dhe b të vazhdueshme gjatë gjithë kohës fushat e përkufizimit funksionin 
Zgjidhje.
Gjeni kufirin e majtë të funksionit në pikën:
.
Prandaj, vlera në pikë duhet të jetë 1:
Le të gjejmë funksionin e dorës së majtë në pikën:
Natyrisht, vlera e funksionit në pikë duhet të jetë e barabartë me:
Përgjigje: funksioni është i vazhdueshëm në të gjithë domenin e përkufizimit për a = 1; b = -3 .
Vetitë themelore të funksioneve të vazhdueshme
Matematika erdhi në konceptin e një funksioni të vazhdueshëm duke studiuar, para së gjithash, ligje të ndryshme të lëvizjes. Hapësira dhe koha janë të pafundme dhe varësitë si shtigje s nga koha t me ligj s = f(t) , jep një shembull të një të vazhdueshme funksione f(t). Temperatura e ujit të nxehtë gjithashtu ndryshon vazhdimisht, është gjithashtu një funksion i vazhdueshëm i kohës: T = f(t) .
V analiza matematikore vërtetohen disa veti të funksioneve të vazhdueshme. Këtu janë më të rëndësishmet nga këto prona.
1. Nëse një funksion i vazhdueshëm në një interval merr vlera të shenjave të ndryshme në skajet e intervalit, atëherë në një pikë të këtij segmenti merr një vlerë të barabartë me zero. Më formalisht, kjo veti jepet në një teoremë të njohur si teorema e parë Bolzano-Cauchy.
2. Funksioni f(x), e vazhdueshme në intervalin [ a, b], merr të gjitha vlerat e ndërmjetme midis vlerave në pikat fundore, domethënë midis f(a) dhe f(b). Më formalisht, kjo veti jepet në një teoremë të njohur si teorema e dytë Bolzano-Cauchy.
VETITË E FUNKSIONET TË VAZHDUESHME NË SEKSION
Konsideroni disa veti të funksioneve që janë të vazhdueshme në një interval. Ne i paraqesim këto prona pa prova.
Funksioni y = f (x) quhen e vazhdueshme në një segment [a, b], nëse është i vazhdueshëm në të gjitha pikat e brendshme të këtij segmenti dhe në skajet e tij, d.m.th. në pikë a dhe b, është i vazhdueshëm përkatësisht djathtas dhe majtas.
Teorema 1. Një funksion që është i vazhdueshëm në segmentin [ a, b], të paktën në një pikë të këtij segmenti merr vlerën më të madhe dhe të paktën në një pikë - atë më të vogël.
Teorema thotë se nëse funksioni y = f (x)është e vazhdueshme në segmentin [ a, b], atëherë ka të paktën një pikë x 1 Î [ a, b] të tillë që vlera e funksionit f (x) në këtë pikë do të jetë më e madhja nga të gjitha vlerat e saj në këtë segment: f (x 1) ≥ f (x)... Në mënyrë të ngjashme, ekziston një pikë e tillë x 2, në të cilën vlera e funksionit do të jetë më e vogla nga të gjitha vlerat në segment: f (x 1) ≤ f (x).
Është e qartë se mund të ketë disa pika të tilla, për shembull, figura tregon se funksioni f (x) merr vlerën më të vogël në dy pika x 2 dhe x 2 ".
Komentoni... Deklarata e teoremës mund të bëhet e pasaktë nëse marrim parasysh vlerën e funksionit në intervalin ( a, b). Në të vërtetë, nëse marrim parasysh funksionin y = x në (0, 2), atëherë është i vazhdueshëm në këtë interval, por nuk arrin as vlerat më të mëdha dhe as më të voglat në të: i arrin këto vlera në skajet e intervalit, por skajet nuk i përkasin në rajonin tonë.
Gjithashtu, teorema pushon së qeni e vërtetë për funksionet e ndërprera. Jep një shembull.
Pasoja. Nëse funksioni f (x) e vazhdueshme në [ a, b], atëherë kufizohet në këtë segment.
Teorema 2. Lëreni funksionin y = f (x)është e vazhdueshme në segmentin [ a, b] dhe në skajet e këtij segmenti merr vlera të shenjave të ndryshme, atëherë ka të paktën një pikë brenda segmentit x = C ku funksioni zhduket: f (C)= 0, ku a< C< b
Kjo teoremë ka një kuptim të thjeshtë gjeometrik: nëse pikat e grafikut të një funksioni të vazhdueshëm y = f (x) që korrespondon me skajet e segmentit [ a, b] shtrihen në anët e ndryshme jashtë boshtit kau, atëherë ky grafik të paktën në një pikë të segmentit pret boshtin kau... Funksionet e ndërprera mund të mos e kenë këtë veti.
Kjo teoremë pranon përgjithësimin e mëposhtëm.
Teorema 3 (teorema e vlerës së ndërmjetme). Lëreni funksionin y = f (x)është e vazhdueshme në segmentin [ a, b] dhe f (a) = A, f (b) = B... Pastaj për çdo numër C e përfunduar ndërmjet A dhe B, ka një pikë të tillë brenda këtij segmenti CÎ [ a, b], çfarë f (c) = C.
Kjo teoremë është gjeometrikisht e qartë. Merrni parasysh grafikun e funksionit y = f (x)... Le f (a) = A, f (b) = B... Pastaj çdo vijë të drejtë y = C, ku C- çdo numër ndërmjet A dhe B, do të presë grafikun e funksionit të paktën në një pikë. Abshisa e pikës së kryqëzimit do të jetë ajo vlerë x = C në të cilën f (c) = C.
Kështu, një funksion i vazhdueshëm, duke kaluar nga njëra prej vlerave të tij në tjetrën, kalon domosdoshmërisht nëpër të gjitha vlerat e ndërmjetme. Veçanërisht:
Pasoja. Nëse funksioni y = f (x)është i vazhdueshëm në një interval dhe merr vlerat më të mëdha dhe më të vogla, pastaj në këtë interval merr, të paktën një herë, çdo vlerë ndërmjet vlerave më të vogla dhe më të mëdha.
DERIVATI DHE SHTOJCAT E TIJ. PËRKUFIZIMI I NJË DERIVATIV
Le të kemi një funksion y = f (x), të përcaktuara në një interval. Për çdo vlerë të argumentit x nga ky interval funksioni y = f (x) ka një kuptim të caktuar.
Konsideroni dy vlera të argumentit: origjinalin x 0 dhe e re x.
Diferenca x– x 0 quhet duke rritur argumentin x në pikën x 0 dhe shënohet Δx... Në këtë mënyrë, Δx = x - x 0 (rritja e argumentit mund të jetë pozitiv ose negativ). Nga kjo barazi rezulton se x = x 0 + Δx, d.m.th. vlera fillestare e ndryshores është rritur. Pastaj, nëse në pikën x 0 vlera e funksionit ishte f (x 0 ), pastaj në një pikë të re x funksioni do të marrë vlerën f (x) = f (x 0 + Δx).
Diferenca y - y 0 = f (x) - f (x 0 ) thirrur rritja e funksionit y = f (x) në pikën x 0 dhe shënohet me simbolin Δy... Në këtë mënyrë,
| Δy = f (x) - f (x 0 ) = f (x 0 + Δx) - f (x 0 ) . | (1) |
Zakonisht vlera origjinale e argumentit është x 0 konsiderohet fikse, dhe vlera e re x- variablat. Pastaj y 0 = f (x 0 ) rezulton të jetë konstante, dhe y = f (x)- variabël. Rritjet Δy dhe Δx do të jenë gjithashtu variabla dhe formula (1) tregon se Dyështë funksion i një ndryshoreje Δx.
Le të përpilojmë raportin e rritjes së funksionit me rritjen e argumentit
Le të gjejmë kufirin e këtij raporti në Δx→ 0. Nëse ky kufi ekziston, atëherë ai quhet derivat i këtij funksioni f (x) në pikën x 0 dhe shënoni f "(x 0). Kështu që,
Derivat këtë funksion y = f (x) në pikën x 0 është kufiri i raportit të rritjes së funksionit Δ y në shtimin e argumentit Δ x kur kjo e fundit tenton arbitrarisht në zero.
Vini re se për të njëjtin funksion derivati në pika të ndryshme x mund të marrë vlera të ndryshme, d.m.th. derivati mund të shihet si funksion i argumentit x... Ky funksion shënohet f "(x)
Derivati shënohet me simbole f "(x), y",. Vlera specifike e derivatit në x = a shënohet f "(a) ose y "| x = a.
Veprimi i gjetjes së derivatit të një funksioni f (x) quhet diferencimi i këtij funksioni.
Për të gjetur drejtpërdrejt derivatin sipas përkufizimit, mund të aplikoni sa më poshtë rregull i madh:
Shembuj.
KUJDESI MEKANIK I DERIVATIT
Nga fizika dihet se ligji lëvizje uniforme ka formën s = v t, ku s- rruga e përshkuar deri në pikën e kohës t, v- shpejtësia e lëvizjes uniforme.
Megjithatë, që nga shumica e lëvizjeve që ndodhin në natyrë janë të pabarabarta, pastaj në rastin e përgjithshëm shpejtësia dhe, rrjedhimisht, distanca s do të varet nga koha t, d.m.th. do të jetë në funksion të kohës.
Pra, le të lëvizë një pikë materiale në një vijë të drejtë në një drejtim sipas ligjit s = s (t).
Le të shënojmë një moment në kohë t 0. Deri në këtë pikë, pika ka shkuar në rrugën e saj s = s (t 0 ). Përcaktoni shpejtësinë v momenti material në kohë t 0 .
Për ta bërë këtë, merrni parasysh një moment tjetër në kohë t 0 + Δ t... Ajo korrespondon me shtegun e përshkuar s = s (t 0 + Δ t). Pastaj, për një interval kohor Δ t pika përshkoi rrugën Δs = s (t 0 + Δ t)–s (t).
Merrni parasysh një qëndrim. Quhet shpejtësia mesatare në intervalin kohor Δ t... Shpejtësia mesatare nuk mund të karakterizojë me saktësi shpejtësinë e lëvizjes së një pike në këtë moment t 0 (sepse lëvizja është e pabarabartë). Për të shprehur më saktë këtë shpejtësi të vërtetë duke përdorur Shpejtësia mesatare, ju duhet të merrni një interval kohor më të shkurtër Δ t.
Pra, shpejtësia e lëvizjes në një kohë të caktuar t 0 (shpejtësia e menjëhershme) është kufiri mesatar i shpejtësisë në intervalin nga t 0 deri në t 0 +Δ t kur Δ t→0:
,
ato. shpejtësi të pabarabartëështë derivati kohor i distancës së përshkuar.
KUPTIMI GJEOMETRIK I DERIVATIT
Le të prezantojmë fillimisht përkufizimin e tangjentes në një kurbë në një pikë të caktuar.
Le të kemi një kurbë dhe një pikë fikse mbi të M 0(shih figurën) Konsideroni një pikë tjetër M këtë kurbë dhe vizatoni një sekant M 0 M... Nëse pika M fillon të lëvizë përgjatë kurbës, dhe pika M 0 mbetet i palëvizshëm, atëherë sekanti ndryshon pozicionin e tij. Nëse me afrim të pakufizuar të pikës M kurbë në pikë M 0 në të dyja anët, sekanti kërkon të zërë pozicionin e një vije të caktuar të drejtë M 0 T pastaj drejt M 0 T quhet tangjentja e lakores në një pikë të caktuar M 0.
Se., tangjente në kurbë në një pikë të caktuar M 0 quhet pozicioni kufizues i sekantit M 0 M kur pikë M priret përgjatë kurbës deri në pikën M 0.
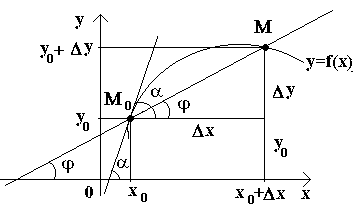
Konsideroni tani funksionin e vazhdueshëm y = f (x) dhe kurba që i përgjigjet këtij funksioni. Në disa vlera X 0 funksioni merr vlerën y 0 = f (x 0). Këto vlera x 0 dhe y 0 në kurbë korrespondon me një pikë М 0 (x 0; y 0). Le të japim një argument x 0 rritje Δ X... Vlera e re e argumentit korrespondon me vlerën e shtuar të funksionit y 0 +Δ y = f (x 0 –Δ x)... E kuptojmë pikën M (x 0+Δ x; y 0+Δ y). Le të vizatojmë një sekant M 0 M dhe shënojmë me φ këndin e formuar nga sekanti me drejtim pozitiv të boshtit kau... Le të hartojmë një relacion dhe ta vërejmë atë.
Nëse tani Δ x→ 0, atëherë për shkak të vazhdimësisë së funksionit Δ në→ 0, dhe për këtë arsye pika M duke lëvizur përgjatë kurbës, i afrohet pikës pafundësisht M 0... Pastaj sekanto M 0 M do të tentojë të marrë pozicionin e tangjentes me lakoren në pikë M 0, dhe këndi φ → α në Δ x→ 0, ku α tregon këndin ndërmjet tangjentes dhe drejtimit pozitiv të boshtit kau... Meqenëse funksioni tan φ varet vazhdimisht nga φ për φ ≠ π / 2, atëherë për φ → α tan φ → tan α dhe, për rrjedhojë, pjerrësia e tangjentes do të jetë:
ato. f" (x)= tg α.
Kështu, gjeometrikisht y" (x 0) paraqet pjerrësinë e tangjentes në grafikun e këtij funksioni në pikë x 0, d.m.th. në këtë vlerë argument x, derivati është i barabartë me tangjenten e këndit të formuar nga tangjentja në grafikun e funksionit f (x) në pikën e duhur М 0 (x; y) me drejtim pozitiv të boshtit kau.
Shembull. Gjeni pjerrësinë e një tangjente në një kurbë y = x 2 në pikë M(-1; 1).
Ne kemi parë tashmë më herët se ( x 2)" = 2X... Por pjerrësia e tangjentes ndaj kurbës është tan α = y"| x = -1 = - 2.
DIFERENCIALITETI I FUNKSIONIVE. VAZHDUESHMËRIA E FUNKSIONIT TË DIFERENCIUAR
Funksioni y = f (x) thirrur të diferencueshme në disa pika x 0 nëse ka një derivat të caktuar në këtë pikë, d.m.th. nëse kufiri i marrëdhënies ekziston dhe është i kufizuar.
Nëse funksioni është i diferencueshëm në çdo pikë të një segmenti [ a; b] ose intervali ( a; b), pastaj thonë se ajo të diferencueshme në segmentin [ a; b] ose, përkatësisht, në intervalin ( a; b).
Teorema e mëposhtme është e vërtetë, duke vendosur një lidhje midis funksioneve të diferencueshme dhe të vazhdueshme.
Teorema. Nëse funksioni y = f (x) të diferencuar në një moment x 0, atëherë është e vazhdueshme në këtë pikë.
Kështu, diferencimi i një funksioni nënkupton vazhdimësinë e tij.
Dëshmi... Nëse 
, pastaj
,
ku α është një sasi infinite e vogël, d.m.th. një sasi që tenton në zero në Δ x→ 0. Por pastaj
Δ y=f "(x 0) Δ x+αΔ x=> Δ y→ 0 në Δ x→ 0, d.m.th. f (x) - f (x 0)→ 0 për x→x 0, dhe kjo do të thotë se funksioni f (x) e vazhdueshme në pikë x 0. Q.E.D.
Kështu, në pikat e ndërprerjes, funksioni nuk mund të ketë një derivat. E kundërta nuk është e vërtetë: ka funksione të vazhdueshme që nuk janë të diferencueshëm në disa pika (d.m.th., nuk kanë një derivat në këto pika).
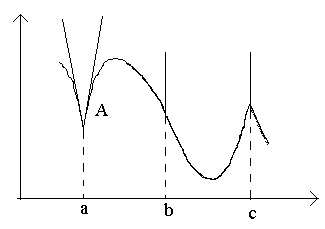
Konsideroni pikat në figurë a, b, c.
Në pikën a në Δ x→ 0, raporti nuk ka kufi (pasi kufijtë e njëanshëm janë të ndryshëm për Δ x→ 0–0 dhe Δ x→ 0 + 0). Në pikën A grafiku nuk ka një tangjente të përcaktuar, por ka dy tangjente të ndryshme të njëanshme me pjerrësi për të 1 dhe për të 2. Këto lloj pikash quhen pika qoshe.
Në pikën b në Δ x→ 0, raporti është një shenjë konstante me vlerë pafundësisht të madhe. Funksioni ka një derivat të pafund. Në këtë pikë, grafiku ka një vijë tangjente vertikale. Lloji i pikës është "pika e lakimit" e tangjentes vertikale.
Në pikën c derivatet e njëanshme janë sasi pafundësisht të mëdha shenjash të ndryshme. Në këtë pikë, grafiku ka dy tangjente vertikale të bashkuara. Lloji - "cusp" me një tangjente vertikale - një rast i veçantë i një pike qoshe.
Përkufizimi... Nëse funksioni f(x) është përcaktuar në segmentin [ a, b], është e vazhdueshme në çdo pikë të intervalit ( a, b), në pikën aështë e vazhdueshme në të djathtë, në pikë bështë e vazhdueshme në të majtë, atëherë themi se funksioni f(x) e vazhdueshme në segment [a, b].
Me fjalë të tjera, funksioni f(x) është e vazhdueshme në segmentin [ a, b] nëse plotësohen tre kushte:
1) "x 0 Î( a, b): f(x) = f(x 0);
2) f(x) = f(a);
3) f(x) = f(b).
Për funksionet që janë të vazhdueshme në një interval, merrni parasysh disa veti, të cilat i formulojmë në formën e teoremave të mëposhtme, pa kryer prova.
Teorema 1... Nëse funksioni f(x) është e vazhdueshme në segmentin [ a, b], atëherë arrin vlerën më të ulët dhe më të lartë në këtë segment.
Kjo teoremë thotë (Fig. 1.15) se në segmentin [ a, b] ekziston një pikë e tillë x 1 që f(x 1) £ f(x) për çdo x nga [ a, b] dhe se ka një pikë x 2 (x 2 I [ a, b]) sikurse " xÎ[ a, b] (f(x 2) ³ f(x)).
Kuptimi f(x 1) është më i madhi për një funksion të caktuar në [ a, b], a f(x 2) - më i vogli. Le të shënojmë: f(x 1) = M, f(x 2) =m... Që për f(x) vlen pabarazia: " xÎ[ a, b] m£ f(x) £ M, atëherë marrim përfundimin e mëposhtëm nga teorema 1.
Pasoja... Nëse funksioni f(x) është e vazhdueshme në një segment, atëherë është e kufizuar në këtë segment.
Teorema 2... Nëse funksioni f(x) është e vazhdueshme në segmentin [ a, b] dhe në skajet e segmentit merr vlera të shenjave të ndryshme, atëherë ekziston një pikë e tillë e brendshme x 0 segment [ a, b], në të cilin funksioni bëhet 0, d.m.th. $ x 0 Î ( a, b) (f(x 0) = 0).
Kjo teoremë thotë se grafiku i funksionit y = f(x) e vazhdueshme në segmentin [ a, b], kalon boshtin kau të paktën një herë nëse vlerat f(a) dhe f(b) kanë shenja të kundërta... Pra, (fig. 1.16) f(a) > 0, f(b) < 0 и функция f(x) zhduket në pika x 1 , x 2 , x 3 .
Teorema 3... Lëreni funksionin f(x) është e vazhdueshme në segmentin [ a, b], f(a) = A, f(b) = B dhe A¹ B... (fig. 1.17). Pastaj për çdo numër C i mbyllur midis numrave A dhe B, ka një pikë të tillë të brendshme x 0 segment [ a, b], çfarë f(x 0) = C.
Pasoja... Nëse funksioni f(x) është e vazhdueshme në segmentin [ a, b], m- vlera më e vogël f(x), M- vlera më e lartë e funksionit f(x) në segmentin [ a, b], atëherë funksioni merr (të paktën një herë) çdo vlerë m e përfunduar ndërmjet m dhe M, dhe për këtë arsye segmenti [ m, M] është bashkësia e të gjitha vlerave të funksionit f(x) në segmentin [ a, b].
Vini re se nëse funksioni është i vazhdueshëm në intervalin ( a, b) ose ka në segmentin [ a, b] pikat e ndërprerjes, atëherë teoremat 1, 2, 3 pushojnë së qeni e vërtetë për një funksion të tillë.
Si përfundim, merrni parasysh një teoremë mbi ekzistencën e një funksioni të anasjelltë.
Kujtoni se një interval kuptohet si një segment, ose një interval, ose një gjysmë-interval, i fundëm ose i pafund.
 |
Teorema 4... Le f(x) është e vazhdueshme në interval X, rritet (ose zvogëlohet) me X dhe ka një sërë kuptimesh Y... Pastaj për funksionin y = f(x) ekziston një funksion invers x= j(y) të përcaktuara në interval Y, i vazhdueshëm dhe në rritje (ose në rënie) me Y me kuptime të shumta X.
Komentoni... Lëreni funksionin x= j(y) është anasjellta e funksionit f(x). Meqenëse argumenti zakonisht shënohet me x, dhe funksioni përmes y, pastaj shkruajmë funksioni i anasjelltë si y =j(x).
Shembulli 1... Funksioni y = x 2 (Fig. 1.8, a) në grup X= }