A jeni këtu tani? =) Jo, nuk po përpiqesha të frikësoja askënd, thjesht tema e integraleve të pahijshme është një ilustrim shumë i mirë se sa e rëndësishme është të mos neglizhosh matematikën e lartë dhe të tjerat. shkencat ekzakte. Gjithçka që ju nevojitet për të zotëruar mësimin gjendet në faqen e internetit – në detaje dhe formë e aksesueshme, do të kishte një dëshirë….
Pra, le të fillojmë me. E thënë në mënyrë figurative, integral jo i duhur- ky është një integral i caktuar "i avancuar", dhe në fakt nuk ka aq shumë vështirësi me to, përveç kësaj, integrali i pahijshëm ka një kuptim shumë të mirë gjeometrik.
Çfarë do të thotë të vlerësosh një integral jo të duhur?
Llogarit integralin e gabuar - kjo do të thotë të gjesh NUMRIN(saktësisht njësoj si në integralin e caktuar), ose të provojë se ajo ndryshon(domethënë, përfundoni me pafundësi në vend të një numri).
Ekzistojnë dy lloje të integraleve jo të duhura.
Integral i papërshtatshëm me kufi(a) të pafund të integrimit
Ndonjëherë një integral i tillë i pasaktë quhet integral i pahijshëm i llojit të parë. NË pamje e përgjithshme një integral i papërshtatshëm me një kufi të pafund më shpesh duket kështu: . Si ndryshon nga një integral i caktuar? Në kufirin e sipërm. Është e pafund: .
Më pak të zakonshme janë integralet me një kufi të poshtëm të pafund ose me dy kufij të pafundëm: , dhe do t'i shikojmë më vonë - kur ta kuptoni :)
Epo, tani le të shohim rastin më të njohur. Në shumicën dërrmuese të shembujve, funksioni integrand të vazhdueshme në mes, dhe ky Fakti i rëndësishëm duhet të kontrollohet fillimisht! Sepse nëse ka boshllëqe, atëherë ka nuanca shtesë. Për saktësi, le të supozojmë se edhe atëherë tipike trapezoid i lakuar do të duket kështu:
Vini re se është e pafundme (jo e kufizuar në të djathtë), dhe integral jo i duhur numerikisht e barabartë me sipërfaqen e saj. Opsionet e mëposhtme janë të mundshme:
1) Mendimi i parë që të vjen ndërmend: “pasi figura është e pafundme, pra 
“, me fjalë të tjera, zona është gjithashtu e pafund. Mund të jetë kështu. Në këtë rast thonë se integrali jo i duhur divergon.
2) Por. Sado paradoksale të tingëllojë, sipërfaqja e një figure të pafundme mund të jetë e barabartë me ... një numër të fundëm! Për shembull: . A mund të jetë kjo e vërtetë? Lehtësisht. Në rastin e dytë, integrali jo i duhur konvergon.
3) Rreth opsionit të tretë pak më vonë.
Në cilat raste ndryshon një integral i papërshtatshëm dhe në cilat raste ai konvergon? Kjo varet nga integranti, dhe shembuj specifikë do ta shqyrtojmë shumë shpejt.
Çfarë ndodh nëse një trapez i lakuar pafundësisht ndodhet nën bosht? Në këtë rast, integrali jo i duhur 
(divergon) ose e barabartë me finalen numër negativ.
Kështu, integrali jo i duhur mund të jetë negativ.
E rëndësishme! Kur ju jepet NDONJË integral i papërshtatshëm për të zgjidhur, atëherë, në përgjithësi, nuk flitet për asnjë zonë dhe nuk ka nevojë të ndërtohet një vizatim. Unë shpjegova kuptimin gjeometrik të integralit të pahijshëm vetëm për ta bërë më të lehtë kuptimin e materialit.
Meqenëse integrali i pahijshëm është shumë i ngjashëm me integralin e caktuar, le të kujtojmë formulën e Newton-Leibniz: 
. Në fakt, formula është gjithashtu e zbatueshme për integrale të pahijshme, vetëm se ajo duhet të modifikohet pak. Qfare eshte dallimi? Në kufirin e sipërm të pafund të integrimit: . Ndoshta, shumë menduan se kjo tashmë i bie aplikimit të teorisë së kufijve, dhe formula do të shkruhet kështu: 
.
Cili është ndryshimi nga një integral i caktuar? Asgje speciale! Ashtu si në integralin e caktuar, ju duhet të jeni në gjendje të gjeni funksionin antiderivativ (integral i pacaktuar) dhe të jeni në gjendje të aplikoni formulën Newton-Leibniz. E vetmja gjë që është shtuar është llogaritja e limitit. Kush e ka të keqen me ta, të nxjerrë një mësim Kufijtë e funksionit. Shembuj zgjidhjesh, sepse më mirë vonë se në ushtri.
Le të shohim dy shembuj klasikë:
Shembulli 1
Për qartësi, unë do të vizatoj një vizatim, megjithëse, e theksoj edhe një herë, në praktikë Nuk ka nevojë të ndërtoni vizatime në këtë detyrë.
Funksioni i integrandit është i vazhdueshëm në gjysmë-interval, që do të thotë se gjithçka është në rregull dhe integrali jo i duhur mund të llogaritet me metodën "standarde".
Zbatimi i formulës sonë 
dhe zgjidhja e problemit duket si kjo:
Kjo do të thotë, integrali i pahijshëm ndryshon, dhe zona e trapezoidit të lakuar me hije është e barabartë me pafundësinë.
Në shembullin e konsideruar, kemi integralin më të thjeshtë të tabelës dhe të njëjtën teknikë për aplikimin e formulës Njuton-Leibniz si në integralin e caktuar. Por kjo formulë do të zbatohet nën shenjën e limitit. Në vend të shkronjës së zakonshme të një ndryshoreje "dinamike", shfaqet shkronja "be". Kjo nuk duhet të ngatërrojë ose turbullojë, sepse çdo shkronjë nuk është më e keqe se standardi "X".
Nëse nuk e kuptoni pse në , atëherë kjo është shumë e keqe, ose nuk i kuptoni kufijtë më të thjeshtë (dhe në përgjithësi nuk e kuptoni se çfarë është një kufi), ose nuk e dini se si duket një grafik funksioni logaritmik. Në rastin e dytë, merrni pjesë në një mësim Grafikët dhe vetitë e funksioneve elementare.
Kur zgjidhni integrale të pahijshme, është shumë e rëndësishme të dini se si duken grafikët e funksioneve themelore elementare!
Detyra e përfunduar duhet të duket diçka si kjo:
“
! Kur përgatisim një shembull, ne gjithmonë ndërpresim zgjidhjen dhe tregojmë se çfarë ndodh me integranin – a është e vazhdueshme në intervalin e integrimit apo jo?. Me këtë ne identifikojmë llojin e integralit jo të duhur dhe justifikojmë veprimet e mëtejshme.
Shembulli 2
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Le të bëjmë vizatimin: 
Së pari, vërejmë sa vijon: integrandi është i vazhdueshëm në gjysmëintervalin. Kapuç. Ne zgjidhim duke përdorur formulën 
:
(1) Marrim integralin më të thjeshtë të funksioni i fuqisë(ky rast i veçantë është në shumë tabela). Është më mirë që menjëherë ta zhvendosni shenjën minus përtej shenjës kufitare, në mënyrë që të mos pengohet në llogaritjet e mëtejshme.
(2) Ne zëvendësojmë kufijtë e sipërm dhe të poshtëm duke përdorur formulën Newton-Leibniz.
(3) Ne tregojmë se në (Zotërinj, kjo duhet të ishte kuptuar shumë kohë më parë) dhe thjeshtojmë përgjigjen.
Këtu zona e një trapezi të lakuar të pafund është një numër i fundëm! E pabesueshme por e vertete.
Shembulli i përfunduar duhet të duket diçka si kjo:
“
Funksioni i integrandit është i vazhdueshëm aktiv
“
Çfarë duhet të bëni nëse hasni një si integrale - me pikë pushimi në intervalin e integrimit? Kjo do të thotë se ka një gabim shtypi në shembull. (Me shumë mundësi), ose rreth një niveli të avancuar trajnimi. Në rastin e fundit, për shkak të vetitë e aditivitetit, duhet të marrim parasysh dy integrale të pahijshme në intervale dhe më pas të merremi me shumën.
Ndonjëherë, për shkak të një gabimi shkrimi ose qëllimi, një integral i gabuar mund nuk ekziston fare, pra, për shembull, nëse vendosim emëruesin e integralit të mësipërm Rrenja katrore nga “x”, atëherë një pjesë e intervalit të integrimit nuk do të përfshihet fare në domenin e përcaktimit të integrandit.
Për më tepër, integrali i papërshtatshëm mund të mos ekzistojë edhe me gjithë "mirëqenien e dukshme". Shembull klasik: . Pavarësisht definicitetit dhe vazhdimësisë së kosinusit, një integral i tillë i papërshtatshëm nuk ekziston! Pse? Është shumë e thjeshtë sepse:
- nuk ekziston kufiri i duhur.
Dhe shembuj të tillë, edhe pse të rrallë, ndodhin në praktikë! Kështu, përveç konvergjencës dhe divergjencës, ekziston edhe një rezultat i tretë i zgjidhjes me një përgjigje të vlefshme: "nuk ka integral të papërshtatshëm".
Duhet të theksohet gjithashtu se përkufizimi i rreptë i një integrali të pahijshëm jepet pikërisht përmes kufirit, dhe ata që dëshirojnë mund të njihen me të në literaturën arsimore. Epo, ne vazhdojmë mësim praktik dhe kaloni në detyra më domethënëse:
Shembulli 3
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Së pari, le të përpiqemi të gjejmë funksionin antiderivativ (integral i pacaktuar). Nëse nuk arrijmë ta bëjmë këtë, atëherë natyrisht nuk do të jemi në gjendje të zgjidhim as integralin e pahijshëm.
Me cilin nga integralet e tabelës është i ngjashëm integrani? Më kujton një arktangjent: 
. Këto konsiderata sugjerojnë se do të ishte mirë të kishim një katror në emërues. Kjo bëhet me zëvendësim.
Le të zëvendësojmë:
Është gjetur integrali i pacaktuar; në këtë rast, nuk ka kuptim të shtohet një konstante.
Është gjithmonë e dobishme të kontrolloni draftin, domethënë të dalloni rezultatin e marrë:
Është marrë integrandi origjinal, që do të thotë se është gjetur saktë integrali i pacaktuar.
Tani gjejmë integralin e papërshtatshëm:
(1) Zgjidhjen e shkruajmë në përputhje me formulën 
. Është më mirë të lëvizni menjëherë konstanten përtej shenjës kufitare në mënyrë që të mos ndërhyjë në llogaritjet e mëtejshme.
(2) Ne zëvendësojmë kufijtë e sipërm dhe të poshtëm në përputhje me formulën Newton-Leibniz. Pse 
në ? Shihni grafikun arktangjent në artikullin e rekomanduar tashmë.
(3) Ne marrim përgjigjen përfundimtare. Një fakt që është i dobishëm të dihet përmendësh.
Studentët e avancuar mund të mos e gjejnë veçmas integralin e pacaktuar dhe të mos përdorin metodën e zëvendësimit, por të përdorin metodën e zëvendësimit të funksionit nën shenjën diferenciale dhe zgjidhjen e integralit të papërshtatshëm "menjëherë". Në këtë rast, zgjidhja duhet të duket diçka si kjo:
“
Integrandi është i vazhdueshëm në . 
“
Shembulli 4
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
! Ky është një shembull tipik dhe integrale të ngjashme gjenden shumë shpesh. Punojeni mirë! Funksioni antiderivativ këtu është mënyra e përzgjedhjes katror i plotë, më shumë detaje rreth metodës mund të gjenden në mësim Integrimi i disa thyesave.
Shembulli 5
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Ky integral mund të zgjidhet në mënyrë të detajuar, domethënë, së pari të gjeni integralin e pacaktuar duke bërë një ndryshim të ndryshores. Ose mund ta zgjidhni "menjëherë" - duke e futur funksionin nën shenjën diferenciale. Kush ka ndonjë trajnim matematikor?
Plotësoni zgjidhjet dhe përgjigjet në fund të orës së mësimit.
Shembuj zgjidhjesh për integrale të pahijshme me një kufi të ulët të pafund të integrimit mund të gjenden në faqe Metoda efikase për zgjidhjen e integraleve jo të duhura. Aty kemi analizuar edhe rastin kur të dy kufijtë e integrimit janë të pafund.
Integrale të pasakta të funksioneve të pakufizuara
Ose integrale të pahijshme të llojit të dytë. Integralet e pahijshme të llojit të dytë "enkriptohen" në mënyrë tinëzare nën integralin e zakonshëm të caktuar dhe duken saktësisht njësoj: Por, ndryshe nga integrali i caktuar, integrani pëson një ndërprerje të pafundme (nuk ekziston): 1) në pikën , 2) ose në pikën , 3) ose në të dyja pikat njëherësh, 4) ose edhe në segmentin e integrimit. Ne do të shohim dy rastet e para; për rastet 3-4 në fund të artikullit ka një lidhje me një mësim shtesë.
Vetëm një shembull për ta bërë të qartë: . Duket se është një integral i caktuar. Por në fakt, ky është një integral i papërshtatshëm i llojit të dytë; nëse e zëvendësojmë vlerën e kufirit të poshtëm në integrand, atëherë emëruesi ynë shkon në zero, domethënë, integrandi thjesht nuk ekziston në këtë pikë!
Në përgjithësi, kur analizohet një integral jo i duhur ju gjithmonë duhet të zëvendësoni të dy kufijtë e integrimit në integrand. Në këtë drejtim, le të kontrollojmë kufirin e sipërm: 
. Gjithçka është në rregull këtu.
Trapezi lakor për llojin e integralit të pahijshëm në shqyrtim duket në thelb kështu:
Këtu gjithçka është pothuajse e njëjtë si në integralin e llojit të parë.
Integrali ynë është numerikisht i barabartë me sipërfaqen e trapezit të lakuar me hije, i cili nuk kufizohet nga lart. Në këtë rast, mund të ketë dy opsione*: integrali i pahijshëm divergjent (zona është e pafundme) ose integrali i pahijshëm është i barabartë me një numër të fundëm (d.m.th., sipërfaqja e një figure të pafundme është e fundme!).
* sipas parazgjedhjes zakonisht supozojmë se ekziston integrali i papërshtatshëm
Mbetet vetëm modifikimi i formulës Njuton-Leibniz. Ai gjithashtu modifikohet me ndihmën e një kufiri, por kufiri nuk priret më në pafundësi, por në vlerën në të djathtë.Është e lehtë të ndiqet nga vizatimi: përgjatë boshtit duhet t'i afrohemi pikës së thyerjes pafundësisht afër në të djathtë.
Le të shohim se si zbatohet kjo në praktikë.
Shembulli 6
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Integrandi ka një ndërprerje të pafundme në një pikë (mos harroni të kontrolloni verbalisht ose në një draft që gjithçka është në rregull me kufirin e sipërm!)
Së pari, le të llogarisim integralin e pacaktuar: 
Zëvendësimi: 
Nëse keni ndonjë vështirësi me zëvendësimin, ju lutemi referojuni mësimit Metoda e zëvendësimit në integral të pacaktuar.
Le të llogarisim integralin e gabuar:
(1) Çfarë ka të re këtu? Praktikisht nuk ka asgjë për sa i përket teknologjisë së zgjidhjeve. E vetmja gjë që ka ndryshuar është hyrja nën ikonën limit: . Shtimi do të thotë që ne po përpiqemi për vlerën në të djathtë (që është logjike - shih grafikun). Një kufi i tillë në teorinë e kufijve quhet kufiri i njëanshëm. Në këtë rast kemi kufiri i dorës së djathtë.
(2) Ne zëvendësojmë kufijtë e sipërm dhe të poshtëm duke përdorur formulën Newton-Leibniz.
(3) Le të merremi me në . Si të përcaktoni se ku po shkon një shprehje? Përafërsisht, thjesht duhet të zëvendësoni vlerën në të, të zëvendësoni tre të katërtat dhe të tregoni se . Le të krehim përgjigjen.
Në këtë rast, integrali i gabuar është i barabartë me një numër negativ. Nuk ka asnjë krim në këtë, vetëm trapezi i lakuar përkatës ndodhet nën bosht.
Dhe tani dy shembuj për zgjidhje të pavarura.
Shembulli 7
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Shembulli 8
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Nëse integrandi nuk ekziston në pikë
Një trapez i lakuar i pafund për një integral kaq të pahijshëm në thelb duket kështu.
Integrali i caktuar si kufi i shumës integrale
mund të ekzistojë (d.m.th. të ketë një vlerë përfundimtare të caktuar) vetëm nëse plotësohen kushtet
Nëse të paktën një nga këto kushte shkelet, atëherë përkufizimi humbet kuptimin e tij. Në të vërtetë, në rastin e një segmenti të pafund, për shembull [ a; ) nuk mund të ndahet në P pjesë me gjatësi të kufizuar 
, e cila, për më tepër, do të prirej në zero me një rritje të numrit të segmenteve. Në rastin e pakufizuar në një moment Me[a;
b] është shkelur kërkesa për zgjedhje arbitrare të pikëve 
në segmente të pjesshme - nuk mund të zgjidhet 
=Me, meqenëse vlera e funksionit në këtë pikë është e papërcaktuar. Megjithatë, edhe për këto raste është e mundur të përgjithësohet koncepti i një integrali të caktuar duke futur një pasazh tjetër në kufi. Quhen integrale mbi intervale të pafundme dhe mbi funksione të ndërprera (të pakufizuara). jo e juaja.
Përkufizimi.
Lëreni funksionin 
është përcaktuar në intervalin [ a; ) dhe është i integrueshëm në çdo interval të fundëm [ a;
b], d.m.th. ekziston 
për këdo b
> a. Lloji limit 
thirrur integral jo i duhur
lloji i parë
(ose një integral jo i duhur mbi një interval të pafundëm) dhe shënoni 
.
Kështu, sipas përkufizimit, 
=
.
Nëse kufiri në të djathtë ekziston dhe është i fundëm, atëherë integrali jo i duhur 
thirrur konvergjente
. Nëse ky kufi është i pafund, ose nuk ekziston fare, atëherë ata thonë se integrali i papërshtatshëm divergon
.
Në mënyrë të ngjashme, ne mund të prezantojmë konceptin e një integrali jo të duhur të funksionit 
përgjatë intervalit (–; b]:
=
.
Dhe integrali jo i duhur i funksionit 
mbi intervalin (–; +) përcaktohet si shuma e integraleve të paraqitura më sipër:
=
+
,
Ku A– pikë arbitrare. Ky integral konvergon nëse të dy termat konvergjojnë, dhe divergjent nëse të paktën njëri prej termave divergjent.
Nga pikëpamja gjeometrike, integrali 
,
, përcakton vlerën numerike të sipërfaqes së një trapezi të pafund kurvilinear të kufizuar më lart nga grafiku i funksionit 
, majtas – drejt 
, nga poshtë – nga boshti OX. Konvergjenca e integralit nënkupton ekzistencën e një zone të kufizuar të një trapezi të tillë dhe barazinë e saj në kufirin e zonës së një trapezi lakor me një mur të lëvizshëm djathtas. 
.
Në rastin e një integrali me një kufi të pafund, mund të përgjithësojmë Formula Njuton-Leibniz:
=
=F( +
) – F( a),
ku F( +
)
=
. Nëse ky kufi ekziston, atëherë integrali konvergjon, përndryshe ai divergjent.
Ne konsideruam një përgjithësim të konceptit të një integrali të caktuar në rastin e një intervali të pafund.
Le të shqyrtojmë tani një përgjithësim për rastin e një funksioni të pakufizuar.
Përkufizimi
Lëreni funksionin 
është përcaktuar në intervalin [ a;
b), është i pakufizuar në disa lagje të pikës b, dhe është i vazhdueshëm në çdo interval 
, ku>0 (dhe, për rrjedhojë, është i integrueshëm në këtë interval, d.m.th. 
ekziston). Lloji limit 
thirrur integral i pahijshëm i llojit të dytë
(ose një integral i gabuar i një funksioni të pakufizuar) dhe shënohet 
.
Kështu, integrali jo i duhur i të pakufizuarit në pikë b funksionet ekzistojnë sipas përkufizimit
=
.
Nëse kufiri në të djathtë ekziston dhe është i fundëm, atëherë thirret integrali konvergjente. Nëse nuk ka kufi të fundëm, atëherë quhet integrali jo i duhur divergjent.
Në mënyrë të ngjashme, ne mund të përcaktojmë integralin e papërshtatshëm të funksionit 
duke pasur një ndërprerje të pafundme në pikë A:
=
.
Nëse funksioni 
ka një boshllëk të pafund në pikën e brendshme Me
, atëherë integrali i papërshtatshëm përcaktohet si më poshtë
=
+
=
+
.
Ky integral konvergon nëse të dy termat konvergjojnë dhe divergjent nëse të paktën një term divergjent.
Nga pikëpamja gjeometrike, integrali jo i duhur i një funksioni të pakufizuar karakterizon gjithashtu zonën e një trapezi të lakuar të pakufizuar:
Meqenëse një integral i papërshtatshëm rrjedh duke kaluar në kufirin nga një integral i caktuar, të gjitha vetitë e një integrali të caktuar mund të transferohen (me përsosjet e duhura) në integrale të pahijshme të llojit të parë dhe të dytë.
Në shumë probleme që çojnë në integrale të pahijshme, nuk është e nevojshme të dihet se me çfarë është i barabartë ky integral, mjafton vetëm të verifikohet konvergjenca apo divergjenca e tij. Për këtë përdorin shenjat e konvergjencës. Shenjat e konvergjencës së integraleve jo të duhura:
1) Shenja e krahasimit.
Le të jetë për të gjithë X
. Atëherë nëse 
konvergon, pastaj konvergon 
, dhe 
. Nëse 
divergon, pastaj divergon dhe 
.
2) Nëse konvergon 
, pastaj konvergon dhe 
(integrali i fundit në këtë rast quhet absolutisht konvergjente).
Shenjat e konvergjencës dhe divergjencës së integraleve jo të duhura të funksioneve të pakufizuara janë të ngjashme me ato të formuluara më sipër.
Shembuj të zgjidhjes së problemeve.
Shembulli 1.
A) 
; b) 
; V) 
G) 
; d) 
.
Zgjidhje.
a) Sipas përkufizimit kemi:
.
b) Po kështu
Prandaj, ky integral konvergon dhe është i barabartë me 
.
c) Sipas përkufizimit 
=
+
, dhe A– numër arbitrar. Le ta vendosim rastin tonë 
, atëherë marrim:
Ky integral konvergon.
Kjo do të thotë se ky integral ndryshon.
e) Le të shqyrtojmë 
. Për të gjetur antiderivativin e integrandit, është e nevojshme të zbatohet metoda e integrimit sipas pjesëve. Pastaj marrim:
Meqenëse asnjëra 
, as 
nuk ekzistojnë, atëherë nuk ekziston dhe
Prandaj, ky integral ndryshon.
Shembulli 2.
Hulumtoni konvergjencën e integralit 
varet nga P.
Zgjidhje.
Në 
ne kemi:
Nëse 
, Kjo 
Dhe. Prandaj, integrali ndryshon.
Nëse 
, Kjo 
, A 
, Pastaj
=,
Prandaj, integrali konvergon.
Nëse 
, Kjo
prandaj, integrali ndryshon.
Kështu, 
Shembulli 3.
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij:
A) 
; b) 
; V) 
.
Zgjidhje.
a) Integrale 
është një integral i papërshtatshëm i llojit të dytë, pasi integrand 
nuk kufizohet në një pikë 
. Pastaj, sipas përkufizimit,
.
Integrali konvergon dhe është i barabartë me 
.
b) Merrni parasysh 
. Edhe këtu integrandi nuk është i kufizuar në pikë 
. Prandaj, ky integral është i papërshtatshëm i llojit të dytë dhe, sipas përkufizimit,
Prandaj, integrali ndryshon.
c) Merrni parasysh 
. Integrand 
pëson një hendek të pafund në dy pika: 
Dhe 
, e para prej të cilave i përket intervalit të integrimit 
. Rrjedhimisht, ky integral është një integral i papërshtatshëm i llojit të dytë. Pastaj, sipas përkufizimit
=
=
.
Prandaj, integrali konvergon dhe është i barabartë me 
.
Integral i caktuar
\[I=\int_a^bf(x)dx \]
u ndërtua nën supozimin se numrat $a,\,b$ janë të fundëm dhe $f(x)$ është një funksion i vazhdueshëm. Nëse shkelet një nga këto supozime, ne flasim për integrale të pahijshme.
10.1 Integrale të pasakta të llojit të parë
Një integral i papërshtatshëm i llojit të parë ndodh kur të paktën një nga numrat $a,\,b$ është i pafund.
10.1.1 Përkufizimi dhe vetitë themelore
Le të shqyrtojmë së pari situatën kur kufiri i poshtëm i integrimit është i fundëm dhe kufiri i sipërm është i barabartë me $+\infty$; ne do të diskutojmë opsionet e tjera pak më vonë. Për $f(x)$, të vazhdueshme për të gjitha $x$ të interesit për ne, merrni parasysh integralin
\fillimi(ekuacioni) I=\int _a^(+\infty)f(x)dx. \quad(19) \label(inf1) \end(ekuacioni)
Para së gjithash, ne duhet të përcaktojmë kuptimin e kësaj shprehjeje. Për ta bërë këtë, ne prezantojmë funksionin
\[I(N)=\int _a^(N)f(x)dx \]
dhe merrni parasysh sjelljen e tij për $N\rightarrow +\infty$.
Përkufizimi. Le të ketë një kufi të kufizuar
\[ A=\lim_(N \rightarrow +\infty)I(N)=\lim_(N \rightarrow +\infty)\int _a^(N)f(x)dx. \]
Atëherë themi se integrali i papërshtatshëm i llojit të parë (19) është konvergjent dhe i është caktuar vlera $A$; vetë funksioni quhet i integrueshëm në intervalin $\left[ a, \, +\infty \djathtas) $. Nëse kufiri i specifikuar nuk ekziston ose është i barabartë me $\pm \infty$, atëherë thuhet se integrali (19) ndryshon.
Merrni parasysh integralin
\[ I=\int _0^(+\infty) \frac(dx)(1+x^2). \]
\[ I(N)=\int _0^(N) \frac(dx)(1+x^2). \]
Në këtë rast dihet antiderivati i funksionit integrand, pra
\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)=arctgx|_0^(N)=arctgN. \]
Dihet se $arctg N \rightarrow \pi /2 $ për $N \rightarrow +\infty$. Kështu, $I(N)$ ka një kufi të fundëm, integrali ynë i papërshtatshëm konvergon dhe është i barabartë me $\pi /2$.
Integralet e parregullta konvergjente të llojit të parë kanë të gjitha vetitë standarde të integraleve të zakonshëm të caktuar.
1. Nëse $f(x)$, $g(x)$ janë të integrueshme në intervalin $\left[ a, \, +\infty \djathtas)$, atëherë shuma e tyre $f(x)+g(x) $ është gjithashtu i integrueshëm në këtë interval, dhe \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx. \] 2. Nëse $f(x)$ është i integrueshëm në intervalin $\left[ a, \, +\infty \right)$, atëherë për çdo konstante $C$ funksioni $C\cdot f(x)$ është gjithashtu i integrueshëm në këtë interval, dhe \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx. \] 3. Nëse $f(x)$ është i integrueshëm në intervalin $\left[ a, \, +\infty \right)$, dhe në këtë interval $f(x)>0$, atëherë \[ \int _a^ (+\infty) f(x)dx\,>\,0. \] 4. Nëse $f(x)$ është i integrueshëm në intervalin $\left[ a, \, +\infty \right)$, atëherë për çdo $b>a$ integrali \[ \int _b^(+ \infty) f(x)dx \] konvergjon dhe \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty ) f( x)dx \] (aditiviteti i integralit mbi intervalin).
Janë të vlefshme edhe formulat për ndryshimin e ndryshores, integrimin sipas pjesëve etj. (me rezerva natyrore).
Merrni parasysh integralin
\fillimi(ekuacioni) I=\int _1^(+\infty)\frac(1)(x^k)\,dx. \quad (20) \label (mod) \fund (ekuacion)
Le të prezantojmë funksionin
\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx. \]
Në këtë rast dihet antiderivati, pra
\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k)|_1^N = \frac(N^(1-k))(1-k)-\frac(1)(1-k) \]
për $k \neq 1$,
\[ I(N)=\int _1^(N)\frac(1)(x)\,dx\,=lnx|_1^N= lnN \]
për $k = 1$. Duke marrë parasysh sjelljen për $N \rightarrow +\infty$, arrijmë në përfundimin se integrali (20) konvergjon për $k>1$ dhe divergjon për $k \leq 1$.
Le të shqyrtojmë tani opsionin kur kufiri i poshtëm i integrimit është i barabartë me $-\infty$, dhe ai i sipërm është i fundëm, d.m.th. le të shohim integralet
\[ I=\int _(-\infty)^af(x)dx. \]
Megjithatë, ky opsion mund të reduktohet në atë të mëparshëm nëse bëjmë një ndryshim të variablave $x=-s$ dhe më pas ndryshojmë kufijtë e integrimit në vende, në mënyrë që
\[ I=\int _(-a)^(+\infty)g(s)ds, \]
$g(s)=f(-s)$. Le të shqyrtojmë tani rastin kur ekzistojnë dy kufij të pafund, d.m.th. integrale
\fillimi(ekuacioni) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(ekuacioni)
dhe $f(x)$ është i vazhdueshëm për të gjithë $x \in \mathbb(R)$. Le ta ndajmë intervalin në dy pjesë: marrim $c \in \mathbb(R)$ dhe shqyrtojmë dy integrale,
\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx. \]
Përkufizimi. Nëse të dy integralet $I_1$, $I_2$ konvergojnë, atëherë integrali (21) quhet konvergjent dhe i caktohet vlera $I=I_1+I_2$ (në përputhje me aditivitetin gjatë intervalit). Nëse të paktën një nga integralet $I_1$, $I_2$ divergjent, integrali (21) quhet divergjent.
Mund të vërtetohet se konvergjenca e integralit (21) nuk varet nga zgjedhja e pikës $c$.
Integralet e pahijshme të llojit të parë me intervale integrimi $\left(-\infty, \, c \right]$ ose $(-\infty, \, +\infty)$ gjithashtu kanë të gjitha vetitë standarde të integraleve të caktuar (me riformulimi përkatës duke marrë parasysh intervalin e integrimit të zgjedhjes).
10.1.2 Testet për konvergjencën e integraleve jo të duhura të llojit të parë
Teorema (shenja e parë e krahasimit). Le të jenë $f(x)$, $g(x)$ të vazhdueshme për $x>a$ dhe $0 a$. Pastaj
1. Nëse integrali \[ \int _a^(+\infty)g(x)dx \] konvergjon, atëherë integrali \[ \int _a^(+\infty)f(x)dx konvergjon. \] 2. Nëse integrali \[ \int _a^(+\infty)f(x)dx \] divergon, atëherë integrali \[ \int _a^(+\infty)g(x)dx divergon. \]
Teorema (kriteri i dytë i krahasimit). Le të jetë $f(x)$, $g(x)$ e vazhdueshme dhe pozitive për $x>a$, dhe le të ketë një kufi të fundëm
\[ \theta = \lim_(x \djathtas +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]
Pastaj integralet
\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]
konvergojnë ose ndryshojnë në të njëjtën kohë.
Merrni parasysh integralin
\[ I=\int _1^(+\infty)\frac(1)(x+\sin x)\,dx. \]
Shprehja e integrandit është një funksion pozitiv në intervalin e integrimit. Më tej, për $x \rightarrow +\infty$ kemi:
$\sin x$ është një korrigjim "i vogël" i emëruesit. Më saktësisht, nëse marrim $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, atëherë
\[ \lim _(x \rightarrow +\infty)\frac(f(x))(g(x))=\lim _(x \rightarrow +\infty)\frac(x)(x+\sin x) =1. \]
Duke zbatuar kriterin e dytë të krahasimit, arrijmë në përfundimin se integrali ynë konvergjon ose divergjent njëkohësisht me integralin.
\[ \int _1^(+\infty)\frac(1)(x)\,dx . \]
Siç u tregua në shembullin e mëparshëm, ky integral ndryshon ($k=1$). Rrjedhimisht, integrali origjinal ndryshon.
Llogaritni integralin e gabuar ose vendosni konvergjencën (divergjencën) e tij.
1. \[ \int _(0)^(+\infty)e^(-ax)\,dx. \] 2. \[ \int _(0)^(+\infty)xe^(-x^2)\,dx. \] 3. \[ \int _(-\infty)^(+\infty)\frac(2xdx)(x^2+1). \] 4. \[ \int _(0)^(+\infty)\frac(xdx)((x+2)^3). \] 5. \[ \int _(-\infty)^(+\infty)\frac(dx)(x^2+2x+2). \] 6. \[ \int _(1)^(+\infty)\frac(lnx)(x^2)\,dx. \] 7. \[ \int _(1)^(+\infty)\frac(dx)((1+x)\sqrt(x)). \] 8. \[ \int _(0)^(+\infty)e^(-\sqrt(x))\,dx. \] 9. \[ \int _(0)^(+\infty)e^(-ax)\cos x\,dx. \] 10. \[ \int _(0)^(+\infty)\frac(xdx)(x^3+1). \]
Integral jo i duhur me kufi të pafund integrimi
Ndonjëherë një integral i tillë i papërshtatshëm quhet edhe një integral jo i duhur i llojit të parë..gif" width="49" height="19 src=">.
Më pak të zakonshme janë integralet me një kufi të poshtëm të pafund ose me dy kufij të pafund: .
Ne do të shqyrtojmë rastin më të njohur https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Jo jo gjithmonë. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">
Le të paraqesim në vizatim grafikun e funksionit të integrandit. Një grafik tipik dhe një trapez i lakuar për këtë rast duket kështu:
Integral jo i duhurhttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", me fjalë të tjera, zona është gjithashtu e pafund. Mund të jetë kështu. Në këtë rast thonë se integrali jo i duhur divergon.
2) Por. Sado paradoksale të tingëllojë, sipërfaqja e një figure të pafundme mund të jetë e barabartë me ... një numër të fundëm! Për shembull: .. Në rastin e dytë, integrali i pahijshëm konvergon.
Çfarë ndodh nëse një trapezoid i lakuar i pafund ndodhet poshtë boshtit?.gif" width="217" height="51 src=">.
: 
.
Shembulli 1
Funksioni integrand https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, që do të thotë se gjithçka është në rregull dhe integrali i pahijshëm mund të llogaritet duke përdorur " metodë standarde”.
Zbatimi i formulës sonë https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">
Kjo do të thotë, integrali i pahijshëm ndryshon, dhe zona e trapezoidit të lakuar me hije është e barabartë me pafundësinë.
Kur zgjidhni integrale të pahijshme, është shumë e rëndësishme të dini se si duken grafikët e funksioneve themelore elementare!
Shembulli 2
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Le të bëjmë vizatimin: 
Së pari, vërejmë sa vijon: integrandi është i vazhdueshëm në gjysmëintervalin. Mirë..gif" width="327" height="53">
(1) Marrim integralin më të thjeshtë të një funksioni fuqie (ky rast i veçantë gjendet në shumë tabela). Është më mirë që menjëherë ta zhvendosni shenjën minus përtej shenjës kufitare, në mënyrë që të mos pengohet në llogaritjet e mëtejshme.
(2) Ne zëvendësojmë kufijtë e sipërm dhe të poshtëm duke përdorur formulën Newton-Leibniz.
(3) Theksojmë se https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Zotërinj, kjo duhet kuptuar gjatë kohë më parë) dhe thjeshtoni përgjigjen.
Këtu zona e një trapezi të lakuar të pafund është një numër i fundëm! E pabesueshme por e vertete.
Shembulli 3
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Integrandi është i vazhdueshëm në .
Së pari, le të përpiqemi të gjejmë funksionin antiderivativ (integral i pacaktuar).
Me cilin nga integralet e tabelës është i ngjashëm integrani? Më kujton një arktangjent: 
. Këto konsiderata sugjerojnë se do të ishte mirë të kishim një katror në emërues. Kjo bëhet me zëvendësim.
Le të zëvendësojmë:
Është gjithmonë e dobishme të kryeni një kontroll, domethënë të dalloni rezultatin e marrë:
Tani gjejmë integralin e papërshtatshëm:
(1) Zgjidhjen e shkruajmë në përputhje me formulën 
. Është më mirë të lëvizni menjëherë konstanten përtej shenjës kufitare në mënyrë që të mos ndërhyjë në llogaritjet e mëtejshme.
(2) Ne zëvendësojmë kufijtë e sipërm dhe të poshtëm në përputhje me formulën e Newton-Leibniz..gif" width="56" height="19 src=">? Shih grafikun arktangjent në artikullin tashmë të rekomanduar vazhdimisht.
(3) Ne marrim përgjigjen përfundimtare. Një fakt që është i dobishëm të dihet përmendësh.
Studentët e avancuar mund të mos e gjejnë veçmas integralin e pacaktuar dhe të mos përdorin metodën e zëvendësimit, por të përdorin metodën e zëvendësimit të funksionit nën shenjën diferenciale dhe zgjidhjen e integralit të papërshtatshëm "menjëherë". Në këtë rast, zgjidhja duhet të duket diçka si kjo:
“
Funksioni i integrimit është i vazhdueshëm në https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“
Shembulli 4
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
! Ky është një shembull tipik dhe integrale të ngjashme gjenden shumë shpesh. Punojeni mirë! Funksioni antiderivativ gjendet këtu duke përdorur metodën e izolimit të një katrori të plotë.
Shembulli 5
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Ky integral mund të zgjidhet në mënyrë të detajuar, domethënë, së pari të gjeni integralin e pacaktuar duke bërë një ndryshim të ndryshores. Ose mund ta zgjidhni atë "menjëherë" - duke e futur funksionin nën shenjën diferenciale..
Integrale të pasakta të funksioneve të pakufizuara
Ndonjëherë integrale të tilla të pahijshme quhen integrale të pahijshme të llojit të dytë. Integralet e pahijshme të llojit të dytë "enkriptohen" në mënyrë tinëzare nën integralin e zakonshëm të caktuar dhe duken saktësisht të njëjtë: ..gif" width="39" height="15 src=">, 2) ose në pikën , 3) ose në të dyja pikat njëherësh, 4) ose edhe në segmentin e integrimit. Do të shqyrtojmë dy rastet e para, për rastet 3-4 në fund të artikullit ka një lidhje me një mësim shtesë.
Vetëm një shembull për ta bërë të qartë: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, atëherë emëruesi ynë shkon në zero, domethënë, integrandi thjesht nuk ekziston në këtë pikë!
Në përgjithësi, kur analizohet një integral jo i duhur ju gjithmonë duhet të zëvendësoni të dy kufijtë e integrimit në integrand..jpg" alt=" Integral i papërshtatshëm, pikë e ndërprerjes në kufirin e poshtëm të integrimit" width="323" height="380">!}
Këtu gjithçka është pothuajse e njëjtë si në integralin e llojit të parë.
Integrali ynë është numerikisht i barabartë me sipërfaqen e trapezit të lakuar me hije, i cili nuk kufizohet nga lart. Në këtë rast, mund të ketë dy opsione: integrali i pahijshëm divergjent (zona është e pafundme) ose integrali i pahijshëm është i barabartë me një numër të fundëm (d.m.th., sipërfaqja e një figure të pafundme është e fundme!).
Mbetet vetëm modifikimi i formulës Njuton-Leibniz. Ai gjithashtu modifikohet me ndihmën e një kufiri, por kufiri nuk priret më në pafundësi, por për të vlerësuarhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> në të djathtë.
Shembulli 6
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Integrandi ka një ndërprerje të pafundme në një pikë (mos harroni të kontrolloni verbalisht ose në një draft që gjithçka është në rregull me kufirin e sipërm!)
Së pari, le të llogarisim integralin e pacaktuar: 
Zëvendësimi: 
Le të llogarisim integralin e gabuar:
(1) Çfarë ka të re këtu? Praktikisht nuk ka asgjë për sa i përket teknologjisë së zgjidhjeve. E vetmja gjë që ka ndryshuar është hyrja nën ikonën limit: . Shtimi do të thotë që ne po përpiqemi për vlerën në të djathtë (që është logjike - shih grafikun). Një kufi i tillë në teorinë e kufijve quhet kufi i njëanshëm. Në këtë rast kemi një kufi të dorës së djathtë.
(2) Ne zëvendësojmë kufijtë e sipërm dhe të poshtëm duke përdorur formulën Newton-Leibniz.
(3) Le të kuptojmë https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Si të përcaktohet se ku duhet të shkojë shprehja? Duke folur përafërsisht , në ju vetëm duhet të zëvendësoni vlerën, të zëvendësoni tre të katërtat dhe të tregoni se .. Ne krehim përgjigjen.
Në këtë rast, integrali i gabuar është i barabartë me një numër negativ.
Shembulli 7
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Shembulli 8
Llogaritni integralin e gabuar ose përcaktoni divergjencën e tij.
Nëse integrandi nuk ekziston në pikë
Një trapez i lakuar i pafund për një integral kaq të pahijshëm në thelb duket kështu:
Këtu gjithçka është absolutisht e njëjtë, përveç se kufiri ynë priret të për të vlerësuarhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> duhet t'i afrohemi pafundësisht pikës së thyerjes majtas.
Integrale të pahijshme të llojit të parë: përhapjen e konceptit integral i caktuar për rastet e integraleve me kufijtë e sipërm ose të poshtëm të pafundëm të integrimit, ose të dy kufijtë e integrimit janë të pafund.
Integrale të pahijshme të llojit të dytë: zgjerimi i konceptit të një integrali të caktuar në rastet e integraleve të funksioneve të pakufizuara; integrani nuk ekziston në një numër të kufizuar pikash të një segmenti të fundëm integrimi, duke u kthyer në pafundësi.
Per krahasim. Gjatë prezantimit të konceptit të një integrali të caktuar, u supozua se funksioni f(x) është e vazhdueshme në intervalin [ a, b], dhe segmenti i integrimit është i fundëm, domethënë është i kufizuar nga numrat dhe jo nga pafundësia. Disa detyra çojnë në nevojën për të braktisur këto kufizime. Kështu shfaqen integralet e pahijshme.
Kuptimi gjeometrik i integralit jo të duhur Rezulton mjaft thjesht. Në rastin kur grafiku i një funksioni y = f(x) është mbi bosht kau integrali i caktuar shpreh sipërfaqen e një trapezi lakor të kufizuar nga një kurbë y = f(x) , boshti x dhe ordinatat x = a , x = b. Nga ana tjetër, integrali i papërshtatshëm shpreh sipërfaqen e një trapezi lakor të pakufizuar (të pafund) të mbyllur midis vijave y = f(x) (në foton më poshtë - e kuqe), x = a dhe boshti i abshisave.
Integralet e pahijshme përcaktohen në mënyrë të ngjashme për intervalet e tjera të pafundme:
Sipërfaqja e një trapezi të lakuar të pafund mund të jetë një numër i fundëm, në këtë rast integrali i gabuar quhet konvergjent. Zona gjithashtu mund të jetë pafundësi, dhe në këtë rast integrali i gabuar quhet divergjent.
Përdorimi i kufirit të një integrali në vend të vetë integralit të papërshtatshëm. Për të vlerësuar integralin e papërshtatshëm, duhet të përdorni kufirin e integralit të caktuar. Nëse ky kufi ekziston dhe është i fundëm (jo i barabartë me pafundësinë), atëherë integrali i papërshtatshëm quhet konvergjent, dhe përndryshe - divergjent. Se çfarë priret një variabël nën shenjën e kufirit varet nëse kemi të bëjmë me një integral të papërshtatshëm të llojit të parë apo të llojit të dytë. Le të zbulojmë për këtë tani.
Integrale të pahijshme të llojit të parë - me kufij të pafund dhe konvergjencë të tyre
Integrale të pahijshme me kufi të sipërm të pafund
Pra, shkrimi i një integrali jo të duhur ndryshon nga integrali i zakonshëm i caktuar në atë që kufiri i sipërm i integrimit është i pafund.
Përkufizimi. Një integral i papërshtatshëm me një kufi të sipërm të pafund integrimi nga funksion të vazhdueshëm f(x) në intervalin nga a përpara ∞ quhet kufiri i integralit të këtij funksioni me kufirin e sipërm të integrimit b dhe kufiri i poshtëm i integrimit a me kusht që kufiri i sipërm i integrimit të rritet pa kufi, d.m.th.
.
Nëse ky kufi ekziston dhe është i barabartë me një numër dhe jo me pafundësi, atëherë një integral i gabuar quhet konvergjent, dhe si vlerë merret numri me të cilin kufiri është i barabartë. Përndryshe një integral i gabuar quhet divergjent dhe nuk i atribuohet asnjë kuptim.
Shembulli 1. Llogaritni integralin jo të duhur(nëse konvergon).
Zgjidhje. Bazuar në përkufizimin e integralit jo të duhur, gjejmë
Meqenëse kufiri ekziston dhe është i barabartë me 1, atëherë kjo integral i papërshtatshëm konvergjon dhe është e barabartë me 1.
Në shembullin e mëposhtëm, integrani është pothuajse i njëjtë me shembullin 1, vetëm shkalla x nuk është dy, por shkronja alfa, dhe detyra është të studiohet integrali i papërshtatshëm për konvergjencë. Kjo do të thotë, pyetja mbetet për t'u përgjigjur: në cilat vlera të alfa konvergon ky integral i pahijshëm dhe në cilat vlera ndryshon?
Shembulli 2. Shqyrtoni integralin e papërshtatshëm për konvergjencë(kufiri i poshtëm i integrimit është më i madh se zero).
Zgjidhje. Së pari, le të supozojmë se, atëherë
Në shprehjen që rezulton, ne kalojmë në kufirin në:
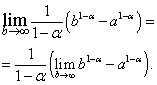
Është e lehtë të shihet se kufiri në anën e djathtë ekziston dhe e barabartë me zero, kur , që është dhe nuk ekziston, kur , që është .
Në rastin e parë, pra kur . Nese atehere 
dhe nuk ekziston.
Përfundimi i studimit tonë është si më poshtë: kjo integral i papërshtatshëm konvergjon në dhe divergon në .
Zbatimi i formulës Njuton-Leibniz për llojin e integralit jo të duhur që studiohet 
, mund të nxirrni formulën e mëposhtme, e cila është shumë e ngjashme me të:
.
Kjo është një formulë e përgjithësuar e Njuton-Leibniz.
Shembulli 3. Llogaritni integralin e gabuar(nëse konvergon).
Kufiri i këtij integrali ekziston:
Integrali i dytë, duke përbërë shumën që shpreh integralin origjinal:
Kufiri i këtij integrali ekziston gjithashtu:
.
Ne gjejmë shumën e dy integraleve, e cila është gjithashtu vlera e integralit të papërshtatshëm origjinal me dy kufij të pafundëm:
Integrale të pahijshme të llojit të dytë - nga funksionet e pakufizuara dhe konvergjenca e tyre
Lëreni funksionin f(x) dhënë në segmentin nga a përpara b dhe është e pakufizuar në të. Supozoni se funksioni shkon në pafundësi në pikë b , ndërsa në të gjitha pikat e tjera të segmentit është i vazhdueshëm.
Përkufizimi. Një integral jo i duhur i një funksioni f(x) në segmentin nga a përpara b quhet kufiri i integralit të këtij funksioni me kufirin e sipërm të integrimit c , nëse kur përpiqet c te b funksioni rritet pa kufi, dhe në pikë x = b funksioni nuk është përcaktuar, d.m.th.
.
Nëse ekziston ky kufi, atëherë integrali i papërshtatshëm i llojit të dytë quhet konvergjent, përndryshe quhet divergjent.
Duke përdorur formulën Newton-Leibniz, ne nxjerrim.